Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Термодинамика и статистическая физика
Содержание
- 1. Термодинамика и статистическая физика
- 2. Лекция № 13 Процессы переноса:
- 3. Если в соседних слоях газа создана и
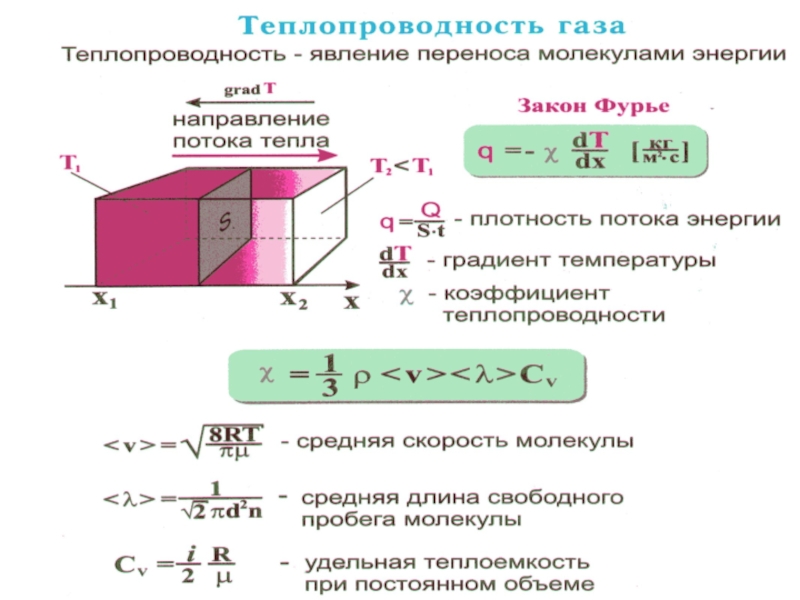
- 4. называется теплопроводностью. Поток тепла пропорционален градиенту температуры: Перенос энергии от более нагретых слоев к более холодным
- 5. Если какое либо тело движется в
- 6. Это явление носит название внутреннее трение или
- 7. В процессе диффузии
- 8. Теплопроводность газов Учение
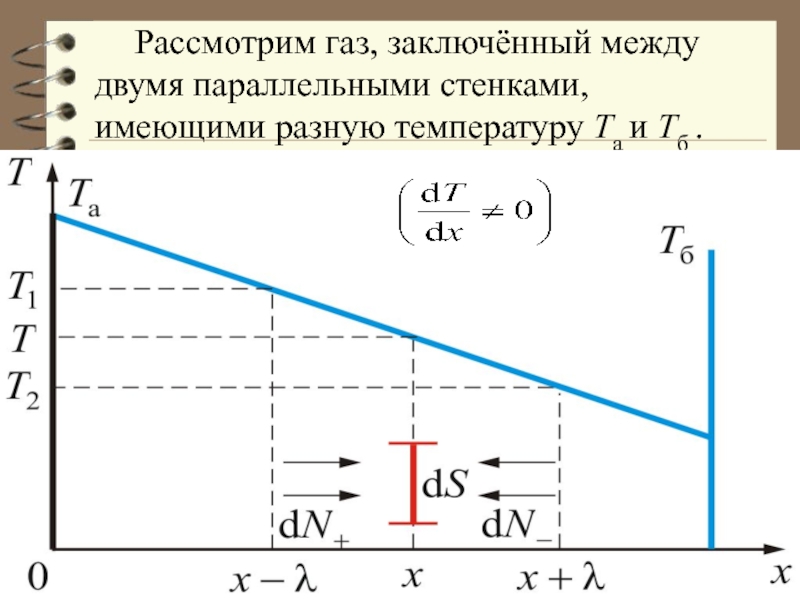
- 9. Рассмотрим газ, заключённый между двумя параллельными стенками, имеющими разную температуру Та и Тб .
- 10. Итак, у нас имеется градиент температуры
- 11. При подсчёте потока тепла введём следующие упрощения:
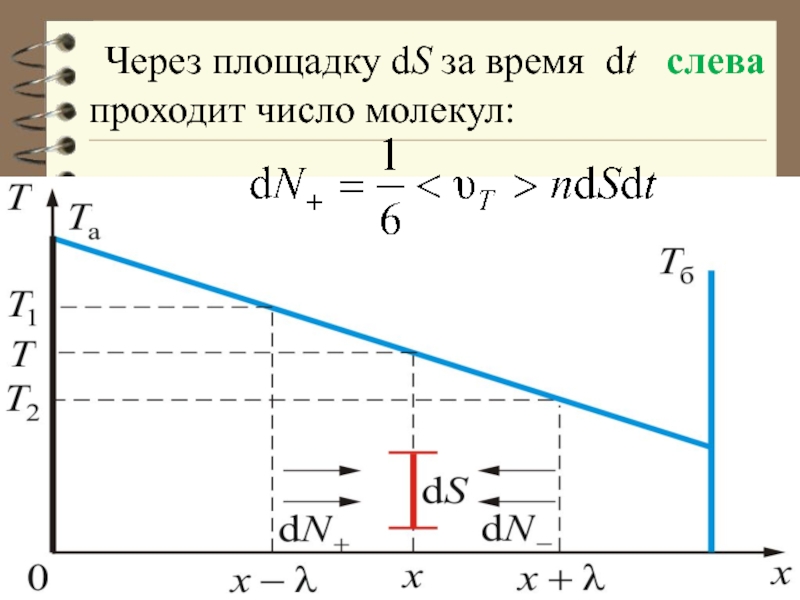
- 12. Через площадку dS за время dt слева проходит число молекул:
- 13. Средняя энергия этих молекул Е – соответствует
- 14. Результирующий поток энергии через dS равен разности
- 15. или
- 16. υТ – тепловая скорость молекул;
- 17. Слайд 17
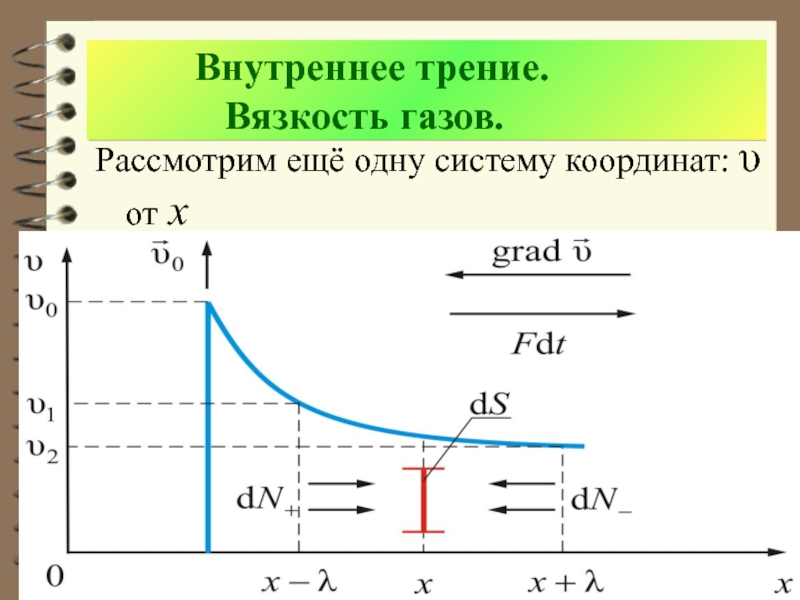
- 18. Внутреннее трение.
- 19. Пусть в покоящемся газе вверх, перпендикулярно оси
- 20. Каждая молекула газа в слое принимает участие
- 21. Средний импульс отдельной молекулы в
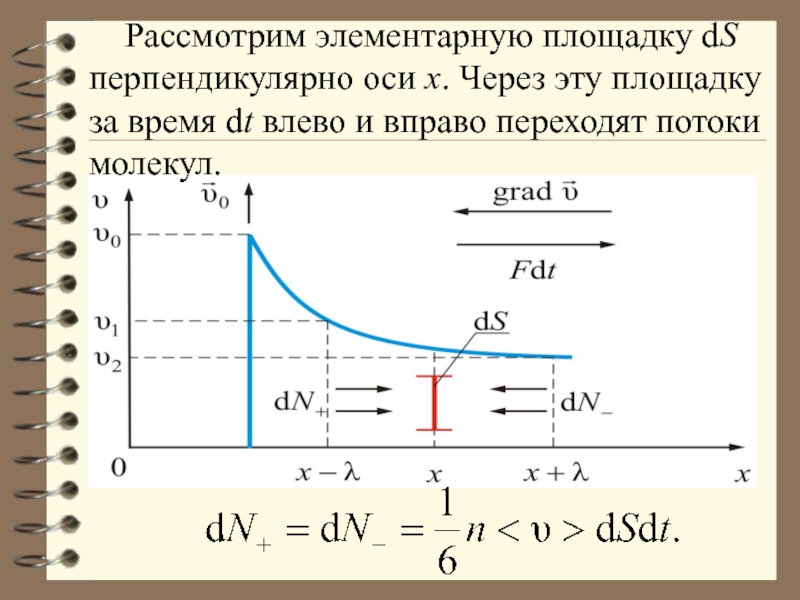
- 22. Рассмотрим элементарную площадку dS перпендикулярно
- 23. Но эти потоки переносят
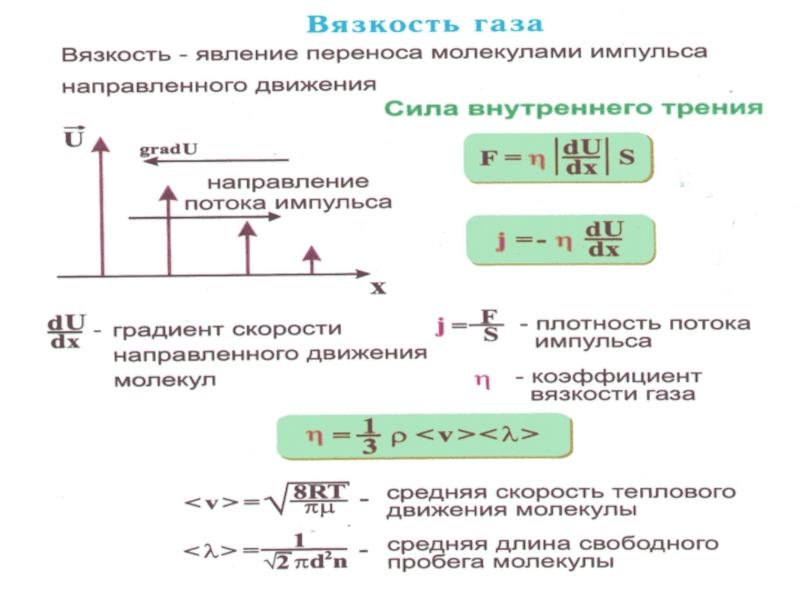
- 24. Закон вязкости был открыт И.
- 25. Сила, действующая на единицу
- 26. Физический смысл коэффици-ента вязкости η в том,
- 27. Слайд 27
- 28. Уравнения и коэффициенты
- 29. или
- 30. Слайд 30
- 31. Лекция закончена !
- 32. Скачать презентанцию
Лекция № 13 Процессы переноса: тепло- проводность и вязкость. 1. Теплопроводность. Закон Фурье. Коэффициент теплопроводности для газов.2. Вязкость. Коэффициент вязкости (внутреннего трения).
Слайды и текст этой презентации
Слайд 2 Лекция № 13
Процессы переноса: тепло- проводность и
вязкость.
Вязкость. Коэффициент вязкости (внутреннего трения).Слайд 3 Если в соседних слоях газа создана и поддерживается разность температур,
то между ними будет происходить обмен тепла. Благодаря хаотическому движению,
молекулы в соседних слоях будут перемешиваться и, их средние энергии будут выравниваться. Происходит перенос энергии от более нагретых слоев к более холодным.Слайд 4называется теплопроводностью.
Поток тепла пропорционален градиенту температуры:
Перенос энергии от более
нагретых слоев к более холодным
Слайд 5 Если какое либо тело движется в газе, то оно
сталкивается с молекулами газа и сообщает им импульс. С другой
стороны, тело тоже будет испытывать соударения со стороны молекул, и получать собственный импульс, но направленный в противоположную сторону. Газ ускоряется, тело тормозиться, то есть, на тело действуют силы трения. Такая же сила трения будет действовать и между двумя соседними слоями газа (или жидкости), движущимися с разными скоростями.Слайд 6 Это явление носит название внутреннее трение или вязкость газа, причём
сила трения пропорциональна градиенту скорости:
Слайд 7 В процессе диффузии происходит перенос вещества, а
при тепло- проводности и при внутреннем трении – перенос энергии.
В основе этих явлений лежит один и тот же механизм – хаотическое движение молекул. Общность механизма, обуславливающего все эти явления переноса, приводит к тому, что их закономерности должны быть похожи друг на друга.Слайд 8 Теплопроводность газов
Учение о теплопроводности начало
развиваться в XVIII в. и получило свое завершение в работах
французского ученого Ж. Фурье (1786 – 1830), опубликовавшего в 1822 г. книгу «Аналитическая теория теплоты».Слайд 9 Рассмотрим газ, заключённый между двумя параллельными стенками, имеющими разную температуру
Та и Тб .
Слайд 10 Итак, у нас имеется градиент температуры
Тогда через газ в
направлении оси х будет идти поток тепла. Хаотично двигаясь, молекулы будут переходить из одного слоя газа в другой, перенося с собой энергию. Это движение молекул приводит к перемешиванию молекул, имеющих различную кинетическую энергию : здесь i – число степеней свободы молекулы.Слайд 11 При подсчёте потока тепла введём следующие упрощения: Среднеарифметическая скорость теплового движения
молекул
Концентрация молекул в соседних слоях одинакова, (хотя на самом деле она различается, что даёт ошибку 10 %).
Слайд 13 Средняя энергия этих молекул Е – соответствует значению энергии в
том месте, где они испытывают последний раз столкновение. Для одной
молекулы газа: Соответственно, справа проходит молекул. Каждая из этих молекул перенесёт энергиюСлайд 14 Результирующий поток энергии через dS равен разности потоков
и , то есть Применяя те же
рассуждения, получим: результирующий поток через единичную площадку в единицу времени равен q и направлен он в сторону противоположную направлению градиента: , - закон ФурьеСлайд 15или
– уравнение теплопроводности Ж.Фурье. Здесь q – тепловой поток; χ – коэффициент теплопроводности, равный: или
Слайд 16 υТ – тепловая скорость молекул;
– удельная теплоемкость при постоянном объеме.
Найдем размерность коэффициента теплопроводности:Слайд 19 Пусть в покоящемся газе вверх, перпендикулярно оси х движется пластинка
со скоростью υ0, причём
(υT – скорость теплового движения молекул). Пластинка увлекает за собой прилегающий слой газа, тот слой – соседний и так далее. Весь газ делится, как бы на тончайшие слои, скользящие вверх тем медленнее, чем дальше они от пластинки. Раз слои газа движутся с разными скоростями, возникает трение. Выясним причину трения в газе.Слайд 20 Каждая молекула газа в слое принимает участие в двух движениях:
тепловом и направленном. Так как направление теплового движения хаотически меняется, то
в среднем вектор тепловой скорости равен нулю При направленном движении вся совокупность молекул будет дрейфовать с постоянной скоростью υ.Слайд 21 Средний импульс отдельной молекулы в слое определяется только
дрейфовой скоростью υ: Но так как молекулы участвуют
в тепловом движении, они будут переходить из слоя в слой. При этом они будут переносить с собой добаво-чный импульс, который будет определяться молекулами того слоя, куда перешла молекула. Перемешивание молекул разных слоёв приводит к выравниванию дрейфовых скоростей разных слоёв, что и проявляется макроскопически как действие сил трения между слоями.Слайд 22 Рассмотрим элементарную площадку dS перпендикулярно оси х. Через
эту площадку за время dt влево и вправо переходят потоки
молекул.Слайд 23 Но эти потоки переносят разный импульс:
и
При переносе импульса от слоя к слою происходит изменение импульса этих слоёв. Это значит, что на каждый из этих слоёв действует сила, равная изменению импульса. Сила эта есть не что иное, как сила трения между слоями газа, движущи-мися с различными скоростями. Отсюда и название – внутреннее трение.Слайд 24 Закон вязкости был открыт И. Ньютоном в 1687
г. Переносимый за время dt импульс
равен: или Отсюда получим силу, действующую на единицу площади поверхности, разделяющей два соседних слоя газа:Слайд 25 Сила, действующая на единицу площади поверхности, разделяющей
два соседних слоя газа: Или, в общем виде:
то уравнение Ньютона. Здесь η – коэффициент вязкости: где D – коэффициент диффузии; ρ – плотность газа.Слайд 26 Физический смысл коэффици-ента вязкости η в том, что он численно
равен импульсу, переносимому в единицу времени через единицу площади при
градиенте скорости равном единице.Слайд 28 Уравнения и коэффициенты
переноса
Сопоставим уравнения
переносаУравнение Фика для диффузии.
Коэффициент диффузии