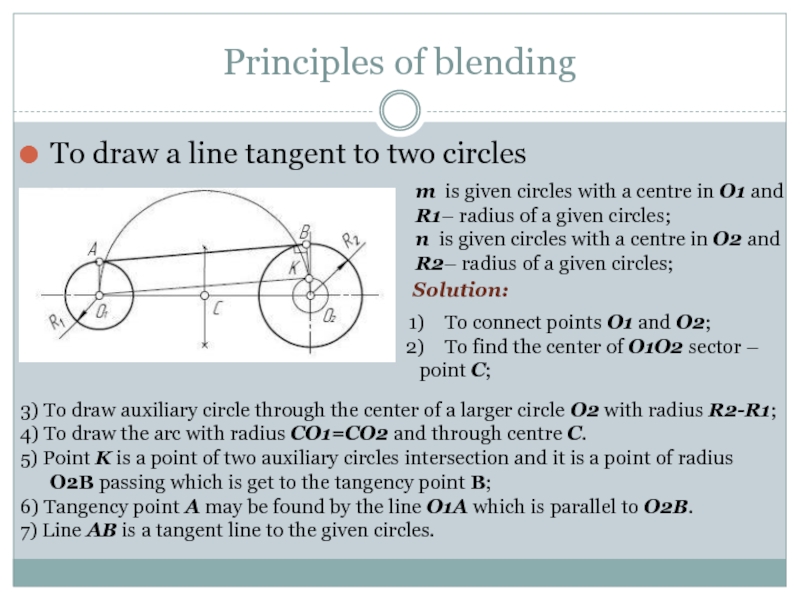
is given circles with a centre in O1 and
R1–
radius of a given circles;
n is given circles with a centre in O2 and
R2– radius of a given circles;
To connect points O1 and O2;
To find the center of O1O2 sector –
point C;
Solution:
3) To draw auxiliary circle through the center of a larger circle O2 with radius R2-R1;
4) To draw the arc with radius CO1=CO2 and through centre C.
5) Point K is a point of two auxiliary circles intersection and it is a point of radius O2B passing which is get to the tangency point B;
6) Tangency point A may be found by the line O1A which is parallel to O2B.
7) Line AB is a tangent line to the given circles.