Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
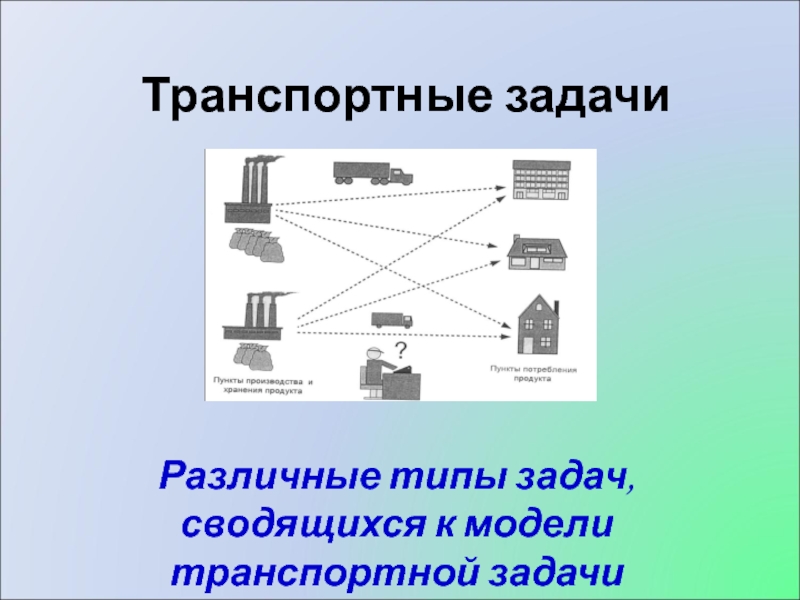
Транспортные задачи Виды
Содержание
- 1. Транспортные задачи Виды
- 2. 1. Замкнутая транспортная задача. Общее предложение равно
- 3. 2. Открытая транспортная задача а)
- 4. 3. Транспортная задача с запретамиПусть для каких-то
- 5. 4. Транспортная задача с фиксированными перевозкамиЕсли объем
- 6. 5. Транспортная задача с ограничениями на пропускную
- 7. 6. Транспортная задача с фиксированными доплатамиПредположим, что
- 8. 6. Транспортная задача с фиксированными доплатами— целевая
- 9. 7. Задача о назначенияхВ процессе управления производством
- 10. 7. Задача о назначенияхОбозначения:сij — показатель эффективности
- 11. 7. Задача о назначениях— целевая функция (минимум
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 21. Замкнутая транспортная задача.
Общее предложение равно общему спросу:
Это необходимое
и достаточное условие существования допустимого плана задачи.
Слайд 32. Открытая транспортная задача
а)
— излишек продукта
Способ сведения к замкнутой задаче.
Вводится фиктивный потребитель. Его потребность bm+1 равна величине избытка продукции, т.е.
«стоимость» перевозок к фиктивному потребителю сi,m+1 =0
б) — дефицит продукта
Способ сведения к замкнутой задаче.
Вводится фиктивный производитель. Его потребность an+1 равна величине дефицита продукции, т.е.
«стоимость» перевозок от фиктивного производителя сn+1,j =0
Слайд 43. Транспортная задача с запретами
Пусть для каких-то пунктов i и
j невозможна (запрещена) транспортировка продукта, то есть хij = 0.
Способ
сведения к замкнутой задаче.Соответствующие стоимости cij делаем достаточно большими числами, чтобы перевозка в данном направлении была невыгодна (приводила к значительному росту суммарной стоимости перевозки).
Слайд 54. Транспортная задача с фиксированными перевозками
Если объем перевозок между пунктами
i и j задан, то вводится дополнительное ограничение: xij =
vij,где vij — заданный объем перевозок.
Слайд 65. Транспортная задача с ограничениями на пропускную способность
Если объем перевозок
из пункта i в пункт j ограничен величиной wij, то
вводится дополнительное ограничение: xij ≤ wij.Слайд 76. Транспортная задача с фиксированными доплатами
Предположим, что в открытой транспортной
задаче имеет место дефицит продукта и для его устранения в
пунктах i=п+1,...,k возможно создание новых мощностей di.Пусть переменные zi = 1, если в пункте i (i=n+1,...,k) вводятся мощности di и zi = 0, если в пункте i мощности не вводятся. Издержки на ввод мощностей di, составляют ui.
С учетом возможности создания новых мощностей транспортная задача может быть записана в следующем виде:
Слайд 86. Транспортная задача с фиксированными доплатами
— целевая функция (минимум затрат
на транспортировку и ввод мощностей);
— ограничения предложения в каждом пункте
производства;— ограничения по величине предложения в каждом новом пункте производства;
— ограничения по величине спроса в каждом пункте потребления;
— условия неотрицательности объемов перевозок.
Помимо непрерывных переменных xij в модель включены булевы переменные zi,. Эта модель является задачей линейного программирования со «смешанными» переменными.
Слайд 97. Задача о назначениях
В процессе управления производством часто возникают задачи
назначения исполнителей на различные виды работ (подбор кадров и назначение
кандидатов на вакантные должности, распределение источников капитальных вложении между различными проектами, распределение экипажей самолетов между авиалиниями).Постановка задачи
Необходимо выполнить N различных работ. Для их выполнения можно привлечь N рабочих. Каждый рабочий за определенную плату готов выполнить любую работу. Каждая работа выполняется одним рабочим.
Требуется так распределить работы между рабочими, чтобы общие затраты на выполнение всех работ были минимальными.
Слайд 107. Задача о назначениях
Обозначения:
сij — показатель эффективности назначения i-го рабочего
на j-й работе, например, издержки выполнения i-м рабочим j-й работы;
xij
— переменная модели (хij = 1, если i-й рабочий используется на j-й работе, и xij = 0 в противном случае)Слайд 117. Задача о назначениях
— целевая функция (минимум издержек на выполнение
всех работ);
— система ограничений, отражающая следующие условия:
а) каждая работа должна
быть выполнена одним рабочим;б) каждый рабочий может быть привлечен к одной работе;
— условия неотрицательности переменных.
Исходной информацией является квадратная матрица с={сij}, элементы которой – показатели эффективности назначений.
Оптимальным планом задачи о назначениях является квадратная матрица назначений х={хij}, , в каждой строке и в каждом столбце которой находится ровно одна единица.