Слайд 2План:
Трехмерное пространство
Пространственные модели
Источники света и материалы
Графический 3D-конвейер
Проекции
Буфер глубины
Программы трехмерной графики
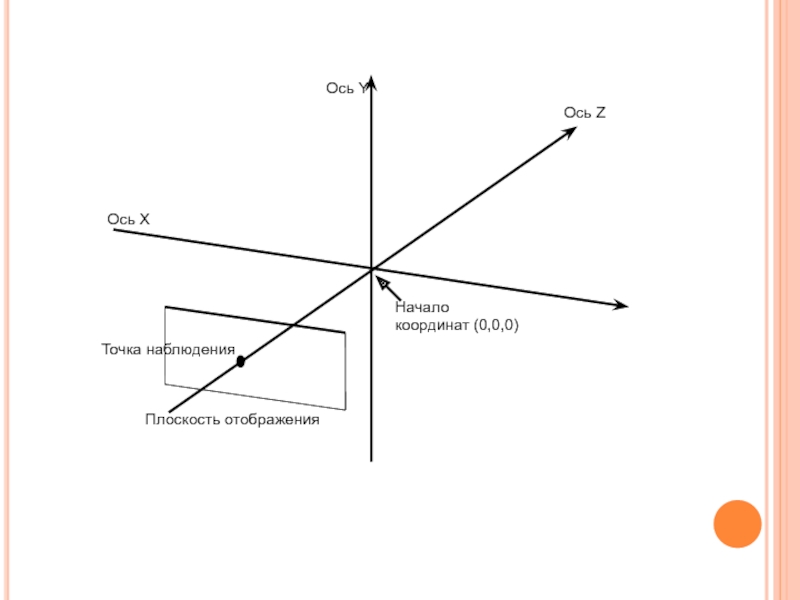
Слайд 3Трехмерное пространство
Трехмерное пространство – это куб в кибернетическом пространстве, создаваемом
в памяти компьютера.
Наименьшей областью трехмерного пространства, которая может быть
занята объектом является точка.
Положение каждой точки определяется тройкой чисел, называемых координатами. Одна из них определяет высоту, другая – ширину, третья – глубину положения точки.
Слайд 4Точка наблюдения – позиция в трехмерном пространстве, определяющая положение наблюдателя.
Воображаемая плоскость, проходящая через точку наблюдения перпендикулярно линии взгляда, называется
плоскостью отображения, которая определяет границы области видимой наблюдателю.
Слайд 6В большинстве программ 3D-графики присутствуют следующие сущности трехмерной сцены:
объекты;
наблюдатель
(камера);
источники света;
свойства материалов объекта.
Слайд 7Пространственные модели
Существует три основных типа моделей описания трехмерных объектов:
с
помощью проволочной сетки,
описание объекта поверхностями,
сплошными телами.
Слайд 8проволочная сетка (wire-frame)
Суть: поверхности строится из серий пересекающихся линий,
принадлежащих поверхности объекта. Как правило, в качестве таких линий принято
использовать отрезки прямых.
Достоинством проволочного представления является простой и эффективный способ построения объектов.
Слайд 9Описание объекта поверхностями
Суть: объект представляется в виде тонких поверхностей, под
которым находится пустое незаполненное пространство.
Слайд 10Описание объекта сплошными телами
Суть заключается в представлении сложного объекта в
виде объединения простых объемных примитивов.
Обычно такие примитивы включают кубы,
цилиндры, конусы, эллипсоиды и другие подобные формы.
Слайд 11Пространственные модели
Основой моделирования объемных тел в трехмерном пространстве являются плоские
многоугольники.
Многоугольники бывают выпуклыми и вогнутыми.
Выпуклым называют многоугольник, в котором
линии, проведенные между любыми двумя точками, будут всегда проходить внутри фигуры.
Операции с выпуклыми многоугольниками происходят быстрее и проще.
Слайд 12Для повышения скорости рендеринга на практике многоугольники разбивают на простейшие
фигуры — треугольники, поскольку они обладают двумя важнейшими свойствами: всегда
выпуклые и всегда плоские.
Любой объект в трехмерной графике в конечном итоге предстает как совокупность треугольников.
Треугольник описывается координатами вершин и вектором нормали к его поверхности.
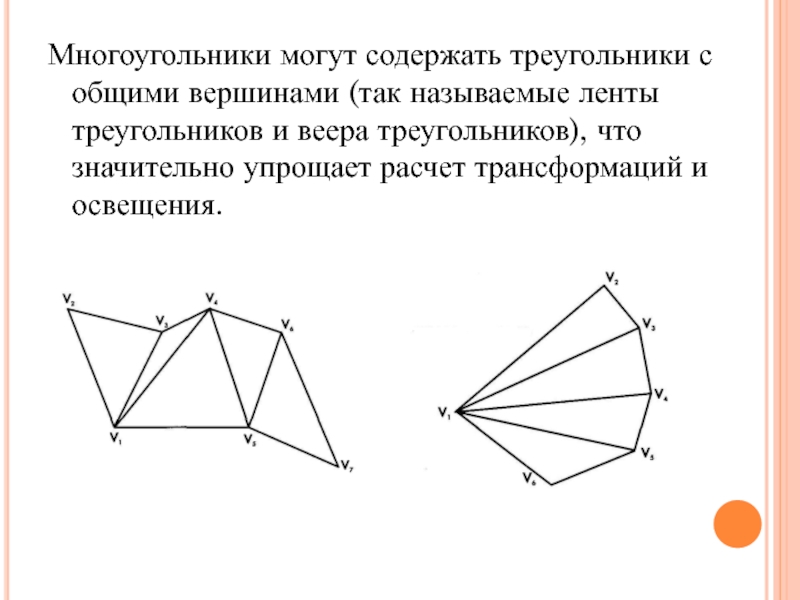
Слайд 13Многоугольники могут содержать треугольники с общими вершинами (так называемые ленты
треугольников и веера треугольников), что значительно упрощает расчет трансформаций и
освещения.
Слайд 14Если вектор нормали направлен к плоскости визуализации, эта сторона объекта
считается передней и проецируется на плоскость. В противном случае треугольник
не отображается, так как считается невидимым.
Операции трансформации объекта (изменение размеров, смещение, вращение) сводятся к расчету новых координат вершин треугольников по отдельности или в составе объединения (для общих вершин).
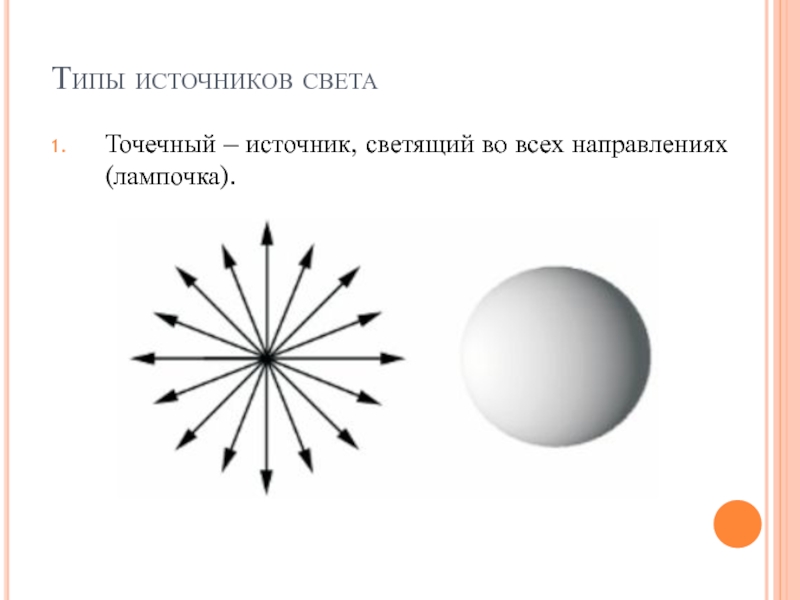
Слайд 15Типы источников света
Точечный – источник, светящий во всех направлениях (лампочка).
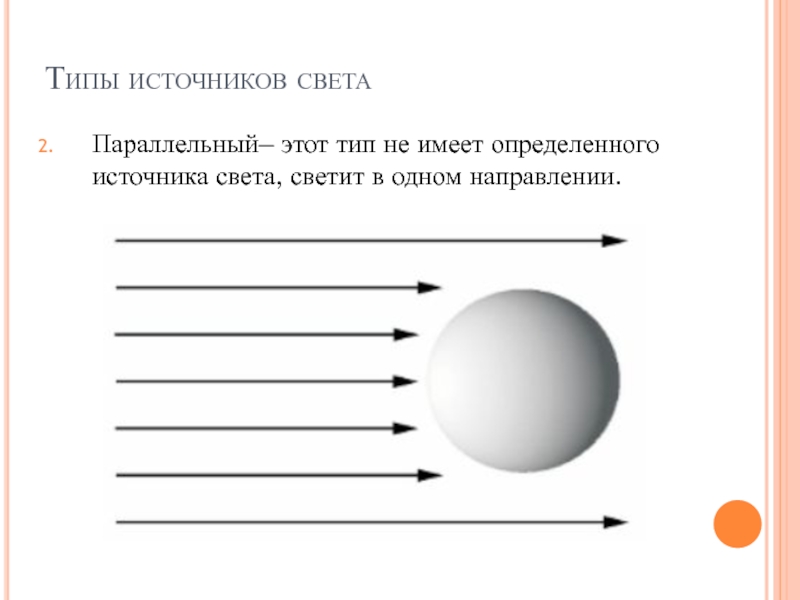
Слайд 16Типы источников света
Параллельный– этот тип не имеет определенного источника света,
светит в одном направлении.
Слайд 17Типы источников света
Прожекторный (нацеленный) – тип, имеющий определенный источник света,
но светящий в заданном направлении в виде направленного конуса (фонарик)
или пирамиды.
Слайд 18Типы отражения света от поверхности
При расчете освещенности грани в компьютерной
графике учитывают следующие типы отражения света от поверхности:
рассеянное,
диффузное,
зеркальное.
Слайд 19Рассеянное отражение
Интенсивность освещения граней объектов рассеянным светом считается постоянной в
любой точке пространства. Это обусловлено тем, что рассеянный свет создается
многочисленными отражениями от различных поверхностей пространства.
Интенсивность рассеянного света выражается как
где Ia- интенсивность рассеянного света, ka- коэффициент рассеянного отражения, зависящий от отражательных свойств материала (поверхности).
При освещении объекта только рассеянным светом, все его грани будут закрашены одинаково, а общие ребра будут неразличимы.
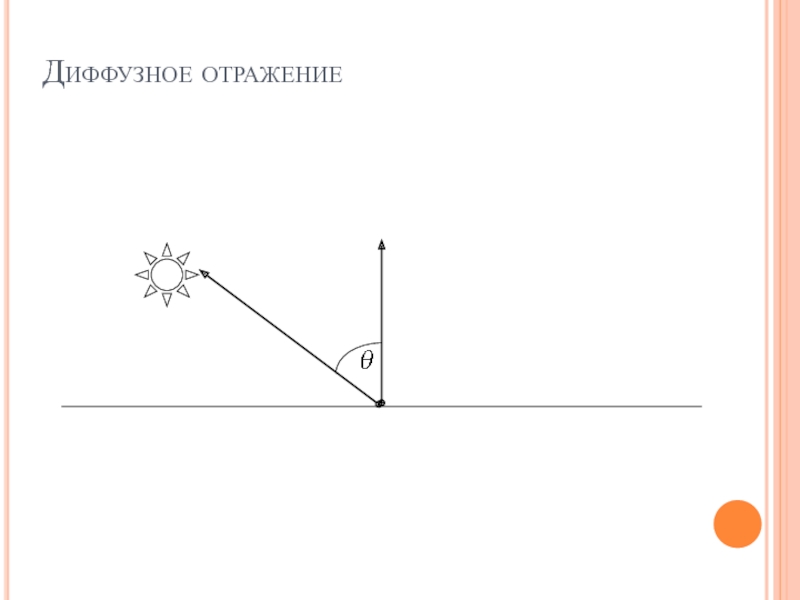
Слайд 20Диффузное отражение
Интенсивность диффузного отражения пропорциональна косинусу угла между нормалью к
поверхности и направлением на источник света.
где Ip – интенсивность
источника света, kd – коэффициент диффузного отражения, - угол падения (угол между направлением на источник света и нормалью к поверхности)
Слайд 22Диффузное отражение
Свойством диффузного отражения является равномерность по всем направлениям отраженного
света.
Поэтому такие объекты имеют одинаковую яркость, вне зависимости от
угла обзора (матовые поверхности).
Слайд 23Диффузное отражение
Интенсивность света обратно пропорционально расстоянию или квадрату расстоянию. Чтобы
это учесть вводят следующую формулу:
где d – расстояние от точки
наблюдения до поверхности,
k – некоторая константа (k≥1)
Слайд 24Зеркальное отражение
Зеркальное отражение можно получить от любой блестящей поверхности. Блестящие
поверхности отражают свет неодинаково по всем направлениям.
При зеркальном отражении на
объекте виден блик, причем блик, как правило, окрашивается в цвет падающего света.
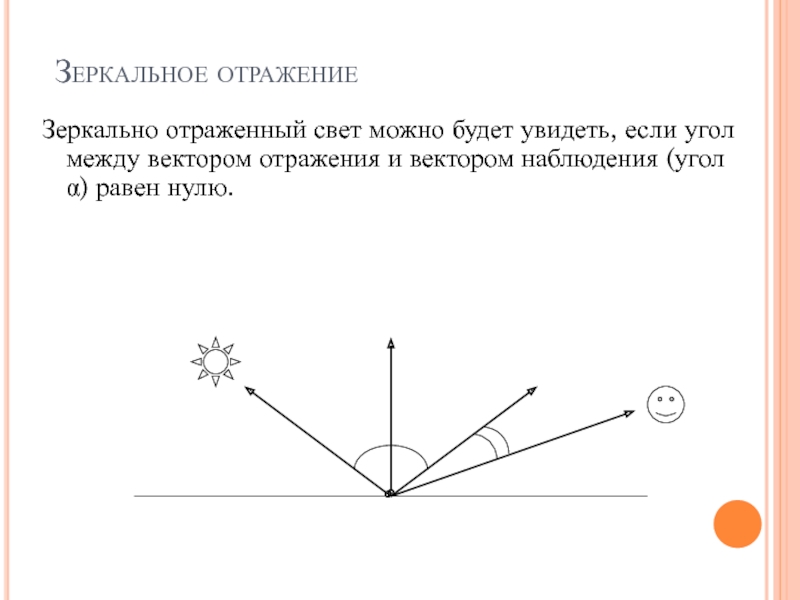
Слайд 25Зеркальное отражение
Зеркально отраженный свет можно будет увидеть, если угол между
вектором отражения и вектором наблюдения (угол ) равен нулю.
Слайд 26Зеркальное отражение
Интенсивность зеркального отражения определяется по формуле:
где Ip – интенсивность
источника света, ks – коэффициент зеркального отражения, n – параметр,
определяющий интенсивность затухания (зависит от вида поверхности). Для идеальной отражающей поверхности n∞.
Слайд 27Зеркальное отражение
Интенсивность зеркального света обратно пропорциональна расстоянию от источника до
грани
где d – расстояние от точки наблюдения до поверхности,
k – некоторая константа (k≥1)
Слайд 28Таким образом, интенсивность грани складывается из трех составляющих: рассеянного света,
диффузного света и зеркального света.
Формула расчета общей интенсивности с
учетом расстояния от наблюдателя до освещенной грани и трех составляющих света записывается как
Слайд 29Материалы
Материалы – это совокупность настроек, определяющих внешний вид материала.
Параметры
материала задаются с помощью числовых параметров или с помощью текстурных
карт.
Материал может присваиваться как ко всей поверхности объекта, так и к отдельным его граням.
Слайд 30Основные свойства материалов:
Цвет (рассеянный, диффузный, зеркальный)
Непрозрачность и прозрачность
Отражение – имитация
отражения окружающих предметов;
Самосвечение;
и т.д.
Слайд 31Текстурные карты – это растровые изображения (в формате jpeg, gif
и т.д.) или процедурные (текстуры генерируемые программным путем с использованием
специальных алгоритмов) изображения, которые можно наносить на поверхность объектов либо использовать для изменения свойств материала.
Слайд 32Технология композитных текстур:
Используются две текстуры: базовая и детальная.
Базовая текстура
содержит основные элементы и обеспечивает общий фон. Детальная текстура содержит
лишь мелкие элементы, необходимые при рассмотрении объекта вблизи.
Обе текстуры смешиваются в пропорции, зависящей от расстояния до плоскости проецирования: дальше или ближе.
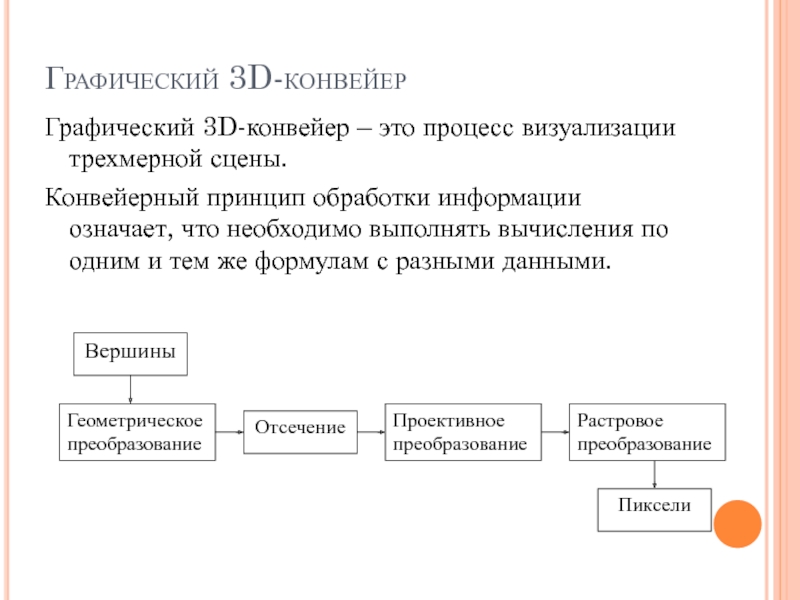
Слайд 33Графический 3D-конвейер
Графический 3D-конвейер – это процесс визуализации трехмерной сцены.
Конвейерный принцип
обработки информации означает, что необходимо выполнять вычисления по одним и
тем же формулам с разными данными.
Слайд 34Этапы графического 3D-конвейера
Геометрические преобразования
Внутреннее представление геометрических объектов должно быть преобразовано
на этой стадии в представление в системе координат устройства отображения
(дисплей, принтер).
Каждое такое преобразование можно представить в матричной форме, причем последовательные преобразования выражаются перемножением (конкатенацией) соответствующих матриц элементарных преобразований. В результате формируется матрица комплексного преобразования.
Слайд 35Этапы графического 3D-конвейера
Отсечение
Вторая важная операция в графическом конвейере – отсечение
(clipping) .
Слайд 36Этапа графического 3D-конвейера
Проективное преобразование
Существует множество видов проективного преобразования, некоторые из
которых позволяют использовать математический аппарата операций с матрицами размером 4x4.
Слайд 37Этапы графического 3D-конвейера
Растровое преобразование
Преобразование описания двухмерных объектов в коды засветки
пикселей в буфере кадра.
Слайд 38Картинная плоскость
Камеры задают четыре типа параметров, однозначно определяющих характеристики создаваемого
ею изображения.
Положение камеры задается положением центра проекции;
Ориентация;
Фокусное расстояние объектива камеры
фактически определяет размер изображения на плоскости проекции;
Размеры (высота и ширина) задней стенки камеры.
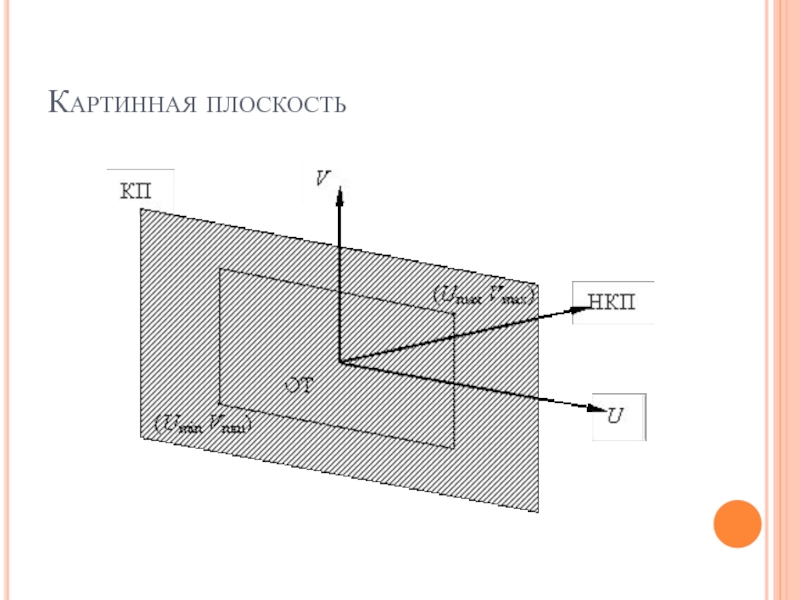
Слайд 39Картинная плоскость
Положение камеры (картинной плоскости) определяется некоторой точкой на плоскости,
которую будем называть опорной точкой (ОТ) и нормалью к картинной
плоскости (НКП).
КП может произвольным образом располагаться относительно проецируемых объектов, заданных в координатах. Она может пересекать их, проходить впереди или позади объектов.
Для того чтобы задать окно камеры, нам необходима система координат на картинной плоскости, которую назовем системой координат UV. Можем задать минимальное и максимальное значения U и V, определяющие окно
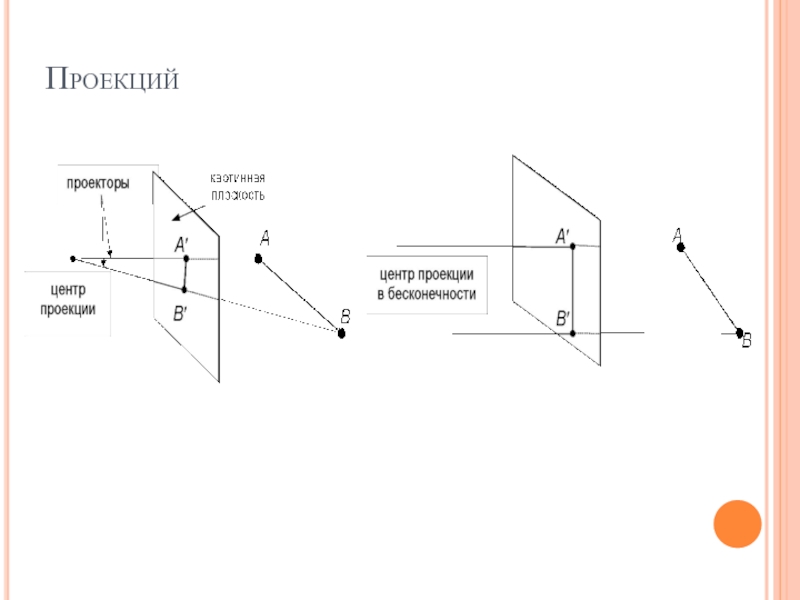
Слайд 41Проекций
В общем случае проекции преобразуют точки, заданные в системе координат
размерностью n, в системы координат размерностью меньше чем n.
Проекция трехмерного
объекта (представленного в виде совокупности точек) строится при помощи прямых проекционных лучей, которые называются проекторами и которые проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.
Слайд 42Проекций
Определенный таким образом класс проекций существует под названием плоских геометрических
проекций, так как проецирование производится на плоскость, а не на
искривленную поверхность и в качестве проекторов используются прямые, а не кривые линии.
Проекции делятся на два основных класса:
параллельные (аксонометрические);
центральные (перспективные).
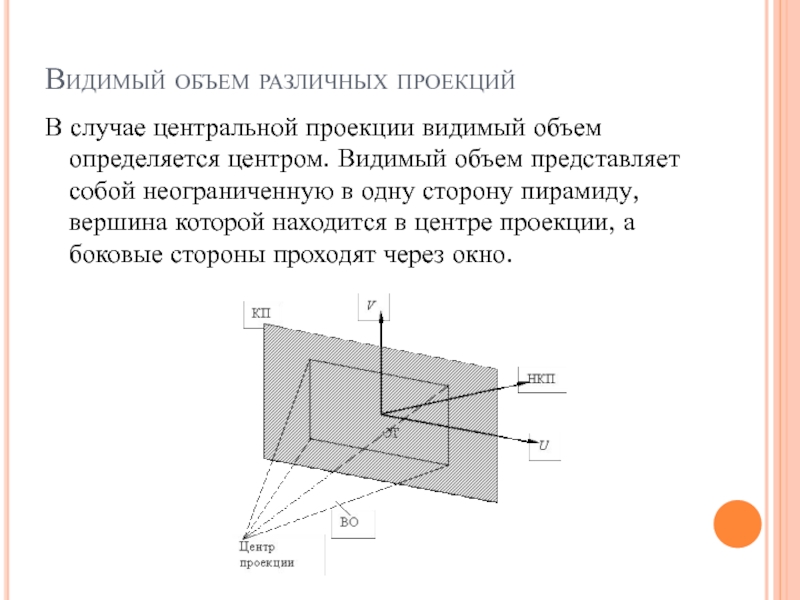
Слайд 44Видимый объем различных проекций
В случае центральной проекции видимый объем определяется
центром. Видимый объем представляет собой неограниченную в одну сторону пирамиду,
вершина которой находится в центре проекции, а боковые стороны проходят через окно.
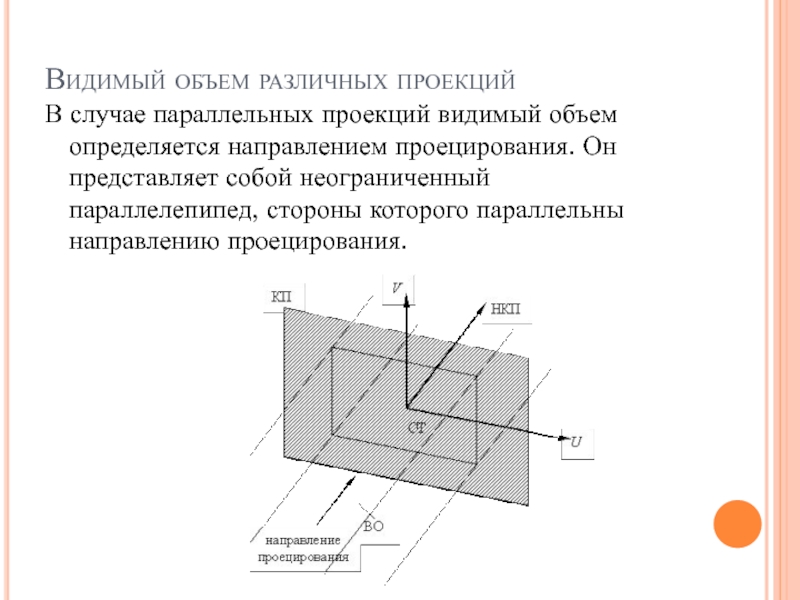
Слайд 45Видимый объем различных проекций
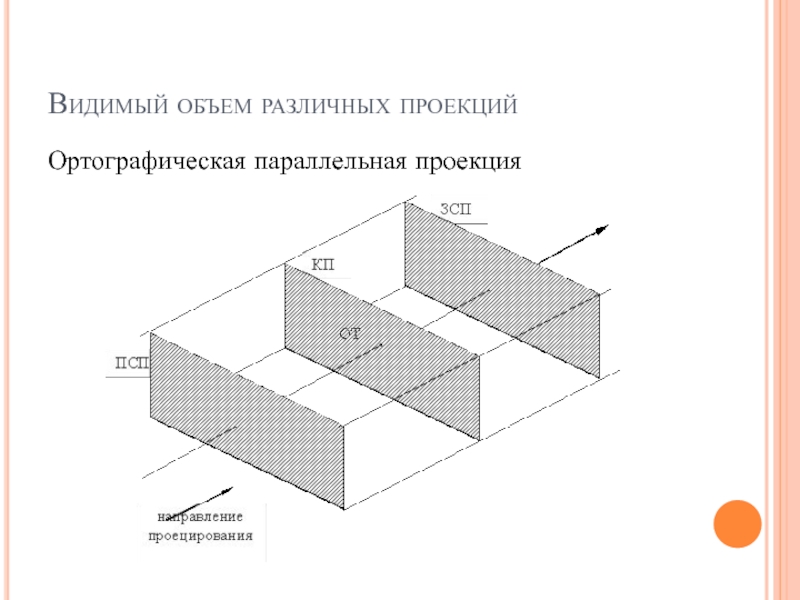
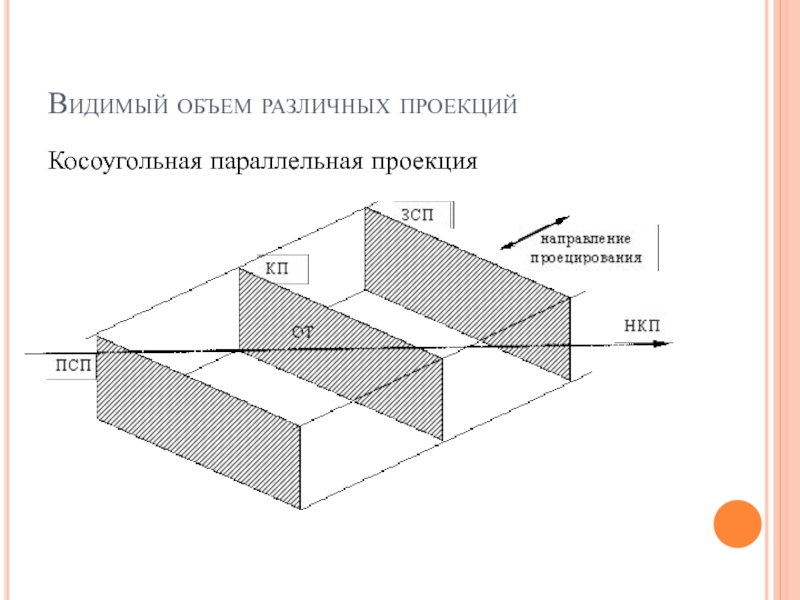
В случае параллельных проекций видимый объем определяется
направлением проецирования. Он представляет собой неограниченный параллелепипед, стороны которого параллельны
направлению проецирования.
Слайд 46Видимый объем различных проекций
В общем случае направление проецирования может не
совпадать с нормалью картинной плоскости.
В случае ортографических параллельных проекций (но
не косоугольных) боковые стороны видимого объема перпендикулярны картинной плоскости.
В некоторых случаях может потребоваться сделать видимый объем конечным. Для этого задаются ПСП (передняя секущая плоскость) и ЗСП (задняя секущая плоскость).
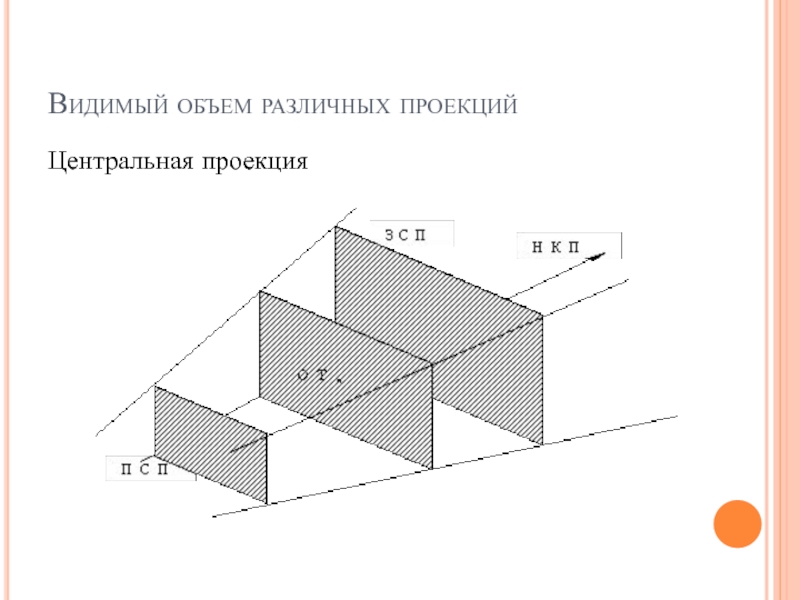
Слайд 47Видимый объем различных проекций
Центральная проекция
Слайд 48Видимый объем различных проекций
Ортографическая параллельная проекция
Слайд 49Видимый объем различных проекций
Косоугольная параллельная проекция
Слайд 50Буфер глубины
Для адекватной визуализации трехмерных объектов в графических библиотеках предусмотрен
так называемый буфер глубины или z-буфер, который представляет собой двумерный
массив, хранящий для каждого растеризуемого пикселя значение координаты z.
Слайд 51Принцип работы буфера глубины
В начале в z-буфер заносятся (очищается) максимально
возможные значения z, а буфер регенерации заполняется значениями пикселей, соответствующими
фону.
Затем каждая грань объекта преобразуется в растровую форму, причем порядок растеризации грани не играет особой роли. При разложении многоугольника в растр для каждой его точки выполняются следующие шаги:
Вычисление глубины (z-координаты) в точке (x,y);
Если z(x,y) меньше чем значение в z-буфере в позиции (x,y) то в z-буфер заносится значение z-координаты растеризуемой точки, а в буфер регенерации помещается обрабатываемый пиксель.
Слайд 52Программы трехмерной графики
3D Studio MAX
Corel Bryce
Adobe Dimension
LightWave 3D
Maya
Poser
Vue dEsprit
Слайд 53Основные возможности 3D Studio MAX:
моделирование геометрической формы любых трехмерных объектов;
имитация
физических свойств материалов объектов, атмосферных явлений, природных явлений;
имитация освещения
трехмерной сцены практически для любых условий;
анимация практически всех параметров объектов;
моделирование постепенных превращений одних объектов в другие, отличающиеся по форме и внешнему виду (морфинг);
моделирование динамических свойств движущихся объектов с учетом их соударений, сил тяжести, ветра или упругости;
применение различных фильтров к изображениям.