Слайд 1Треугольник - удивительная фигура
Слайд 2Цель проекта: изучить историю развития термина «треугольник», узнать новые геометрические
сведения о треугольниках.
Задачи проекта:
Познакомиться с историей возникновения треугольника.
Исследовать геометрические
свойства треугольника.
Показать существование треугольников в природе и применение треугольников в искусстве, архитектуре, окружающей жизни.
Сроки реализации проекта: декабрь-май.
Слайд 3Возникновение и развитие геометрии
Слайд 5 Великий ученый Фалес Милетский
основал одну из прекраснейших наук – геометрию.
Фалес Милетский
имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции.
VI век до нашей эры
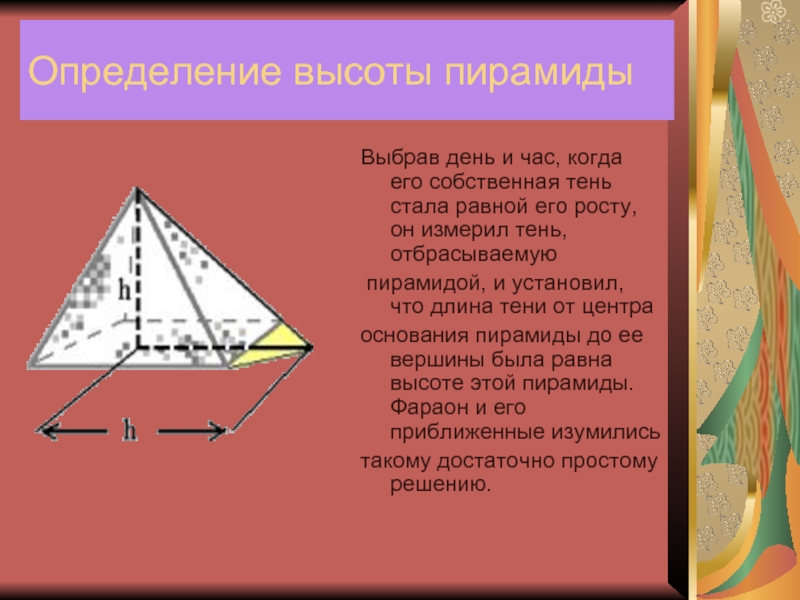
Слайд 6Определение высоты пирамиды
Выбрав день и час, когда его собственная тень
стала равной его росту, он измерил тень, отбрасываемую
пирамидой, и
установил, что длина тени от центра
основания пирамиды до ее вершины была равна высоте этой пирамиды. Фараон и его приближенные изумились
такому достаточно простому решению.
Слайд 7 Фалес решил следующие задачи:
Предложил способ определения расстояния до корабля
на море.
Вычислил высоту египетской пирамиды Хеопса по длине отбрасываемой тени.
Доказал
равенство углов при основании равнобедренного треугольника.
Ввел понятие движения, в частности поворота.
Доказал второй признак равенства треугольников и впервые применял его в задаче.
Теорема Фалеса о равных отрезках, отсекаемых параллельными
прямыми на сторонах угла.
Слайд 8Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по
которой изучали геометрию.
В «Началах» были систематизированы известные к тому времени
геометрические сведения, и геометрия впервые предстала как математическая наука.
Слайд 9“Египетский” треугольник
Среди бесконечного количества возможных прямоугольных треугольников, особый интерес всегда
вызывали так называемые «пифагоровы треугольники», стороны которых являются целыми числами.
«Священным» или «египетским» назывался прямоугольный треугольник со сторонами 3,4,и 5.
Слайд 10Типы треугольников
По видам углов
По числу равных сторон
Остроугольные
Тупоугольные
Прямоугольные
Разносторонние
Равнобедренные
равносторонние
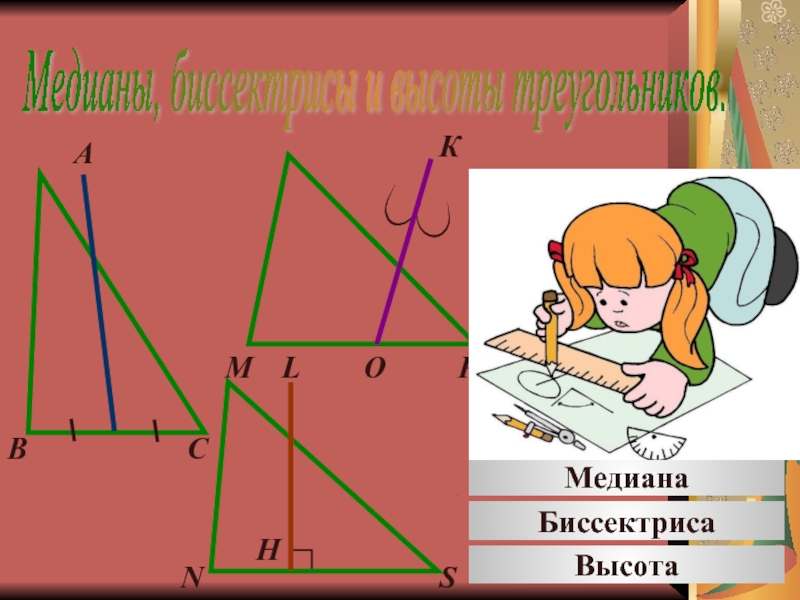
Слайд 11Медианы, биссектрисы и высоты треугольников.
А
К
В
М
С
Р
О
N
L
S
H
Медиана
Биссектриса
Высота
Слайд 12Свойства равнобедренного треугольника.
А
М
В
К
С
N
Углы при
основании.
Медиана, высота,
биссектриса.
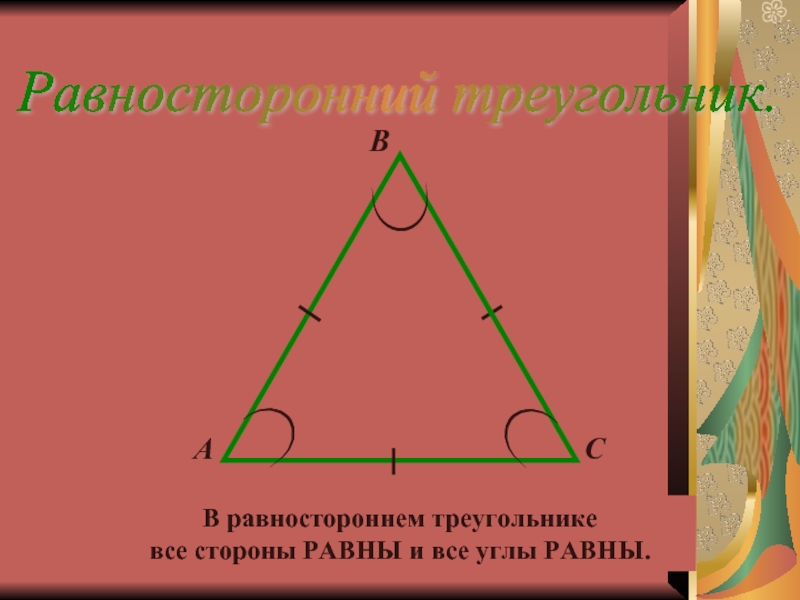
Слайд 13Равносторонний треугольник.
А
В
С
В равностороннем треугольнике
все стороны РАВНЫ и все
углы РАВНЫ.
Слайд 14
Первый признак равенства треугольников:
Если две стороны и угол между ними
одного треугольника соответственно равны двум сторонам и углу между ними
другого треугольника, то такие треугольники равны
Если AB=A1B1, AC=A1C1, ∠A= ∠ A1, то △ABC= △A1B1C1
Признаки равенства треугольников
Слайд 15
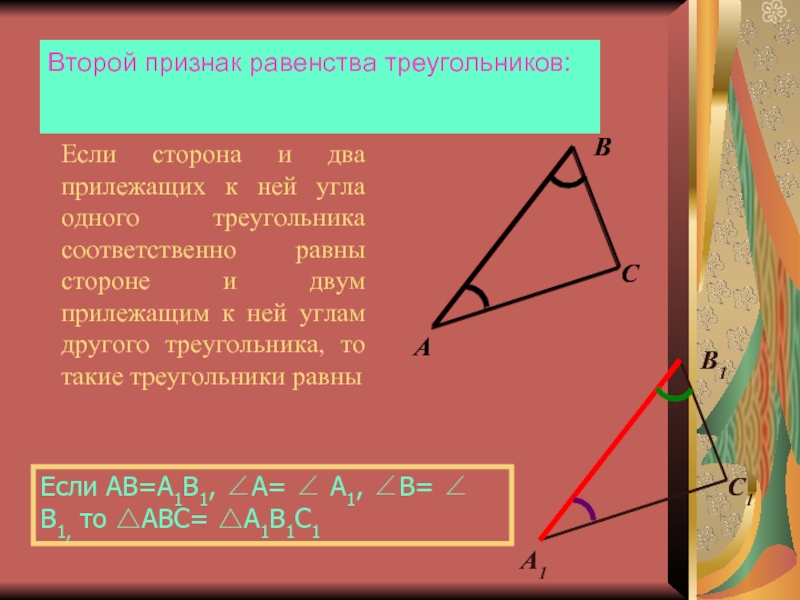
Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники равны
Если AB=A1B1, ∠A= ∠ A1, ∠B= ∠ B1, то △ABC= △A1B1C1
Второй признак равенства треугольников:
A1
B1
C1
B
C
A
Слайд 16
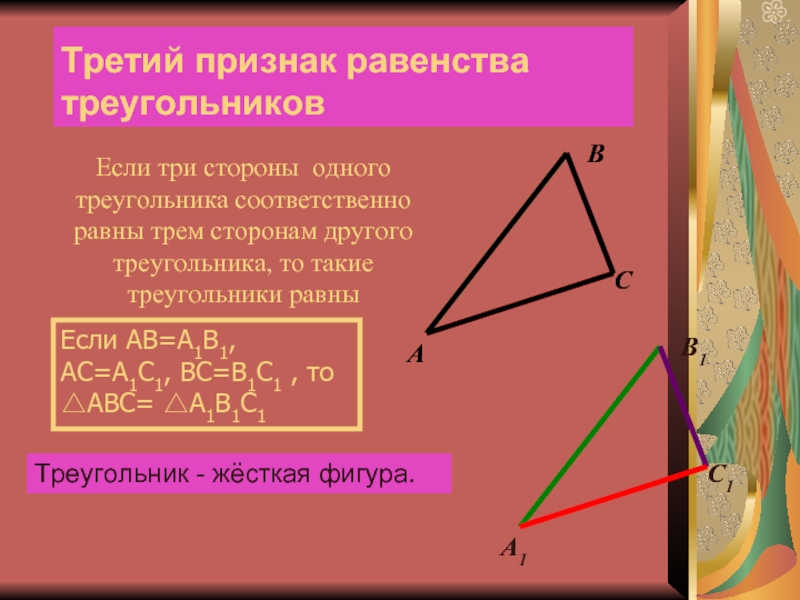
Если три стороны одного треугольника соответственно равны трем сторонам другого
треугольника, то такие треугольники равны
B
A
C
Если AB=A1B1, AC=A1C1, BC=B1C1 , то
△ABC= △A1B1C1
Третий признак равенства треугольников
B1
A1
C1
Треугольник - жёсткая фигура.
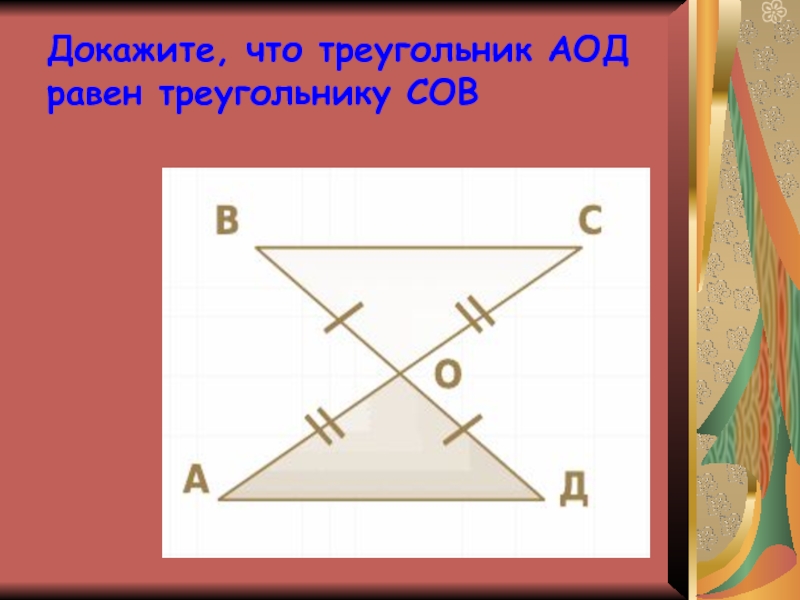
Слайд 17Докажите, что треугольник АОД равен треугольнику СОВ
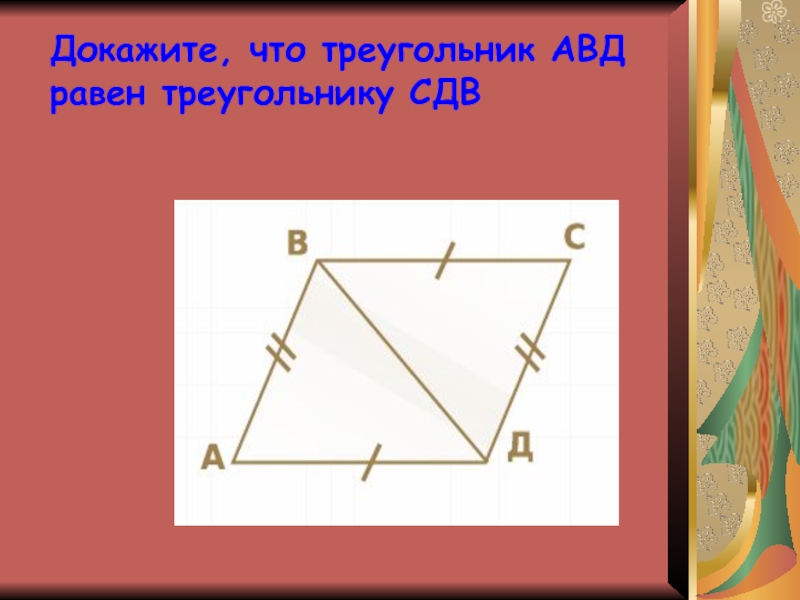
Слайд 18Докажите, что треугольник АВД равен треугольнику СДВ
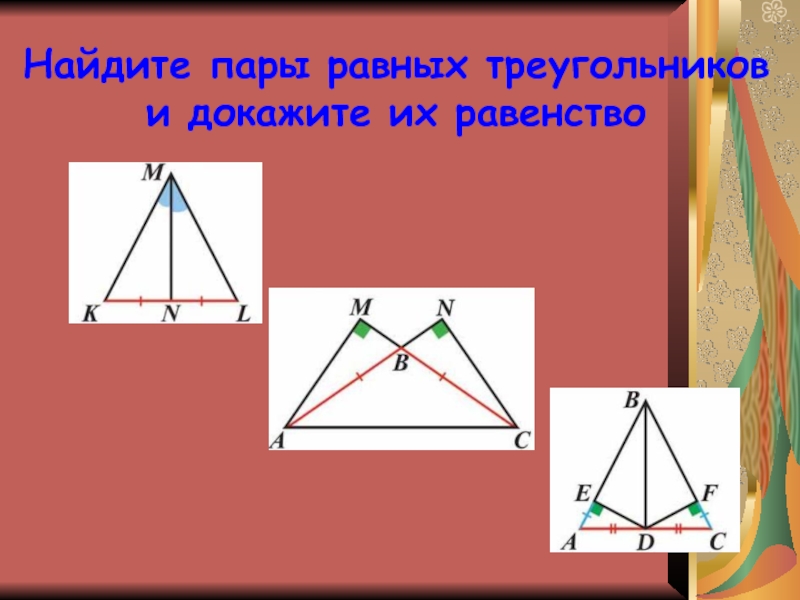
Слайд 19Найдите пары равных треугольников и докажите их равенство
Слайд 20
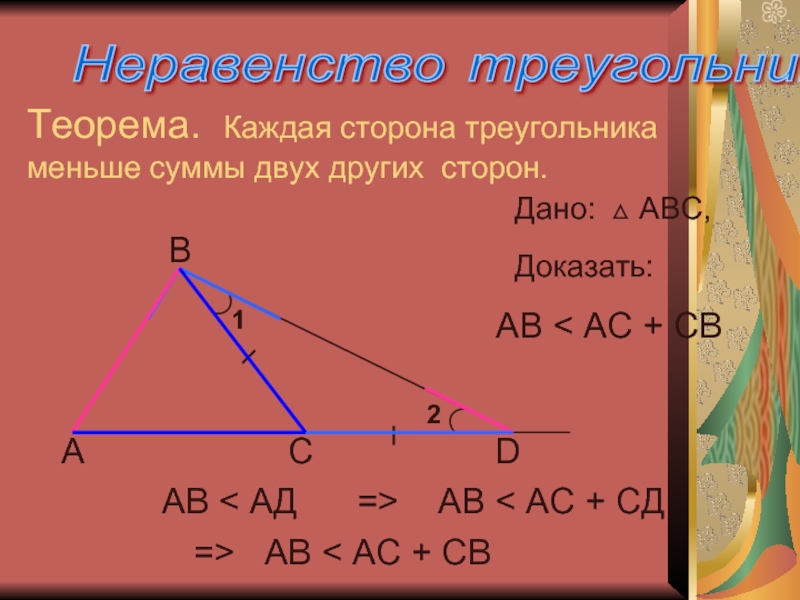
Теорема. Каждая сторона треугольника меньше суммы двух других сторон.
А
В
С
D
АВ
АС + СВ
Доказать:
1
2
АВ < АД
=> АВ < АС +
СД
=> АВ < АС + СВ
Дано: АВС,
Неравенство треугольника
Слайд 21Для любых трех точек А, В и С, не лежащих
на одной прямой, справедливы неравенства:
АВ < AC + CB
AC
AB + BC
BC < BA + AC
Неравенство треугольника
Слайд 22Теорема о сумме углов треугольника.
А
В
С
Слайд 23Внешний угол треугольника. Свойство.
А
В
С
Внешний угол треугольника равен сумме
двух углов
треугольника, не смежных с ним.
D
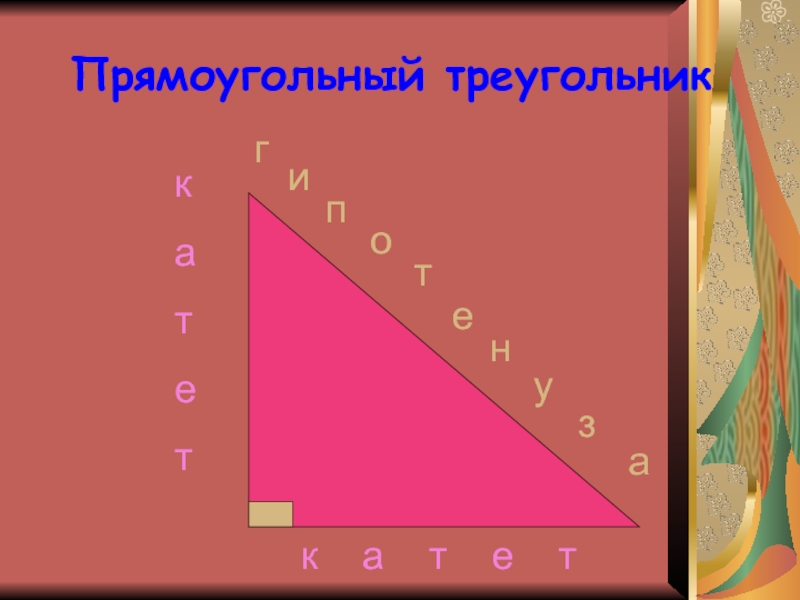
Слайд 24Прямоугольный треугольник
к
а
т
е
т
к а т е
т
г
и
п
о
т
е
н
у
з
а
Слайд 25Некоторые свойства прямоугольных треугольников
сумма двух острых углов прямо-
угольного треугольника равна 90°
катет прямоугольного треуголь -
ника,
лежащий против угла в 30°,
равен половине гипотенузы
если катет прямоугольного треугольника
равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°
30о
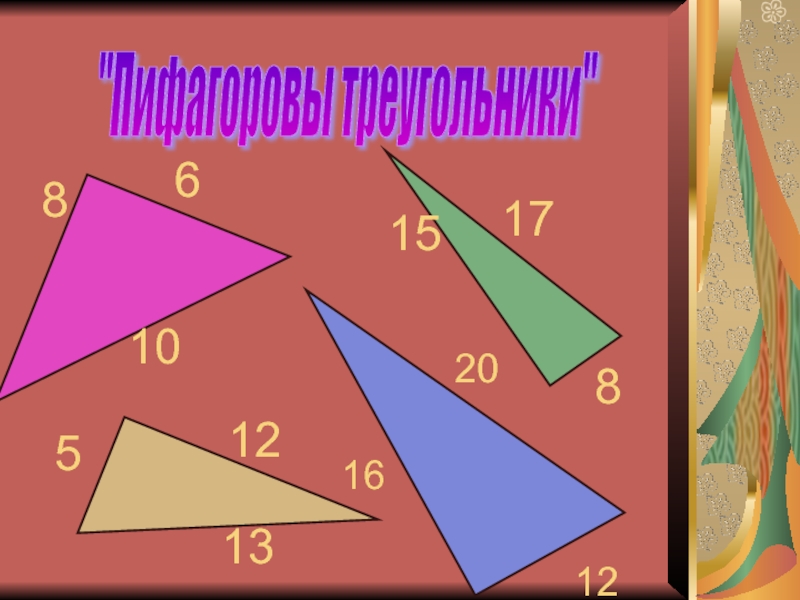
Слайд 26
12
5
15
8
17
"Пифагоровы треугольники"
8
10
6
13
20
16
12
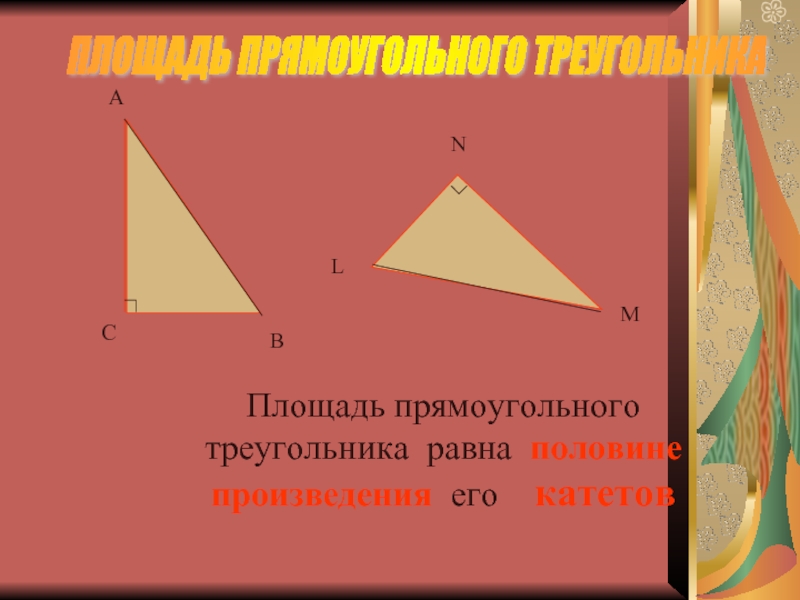
Слайд 27ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
A
C
B
L
M
N
Площадь прямоугольного
треугольника равна половине произведения его катетов
Слайд 28решение задач
2. Пусть а –основание, h – высота,
S – площадь треугольника. Заполнить таблицу.
1. Найти площадь прямоугольного треугольника, если его катеты равны 4 см и 11 см.
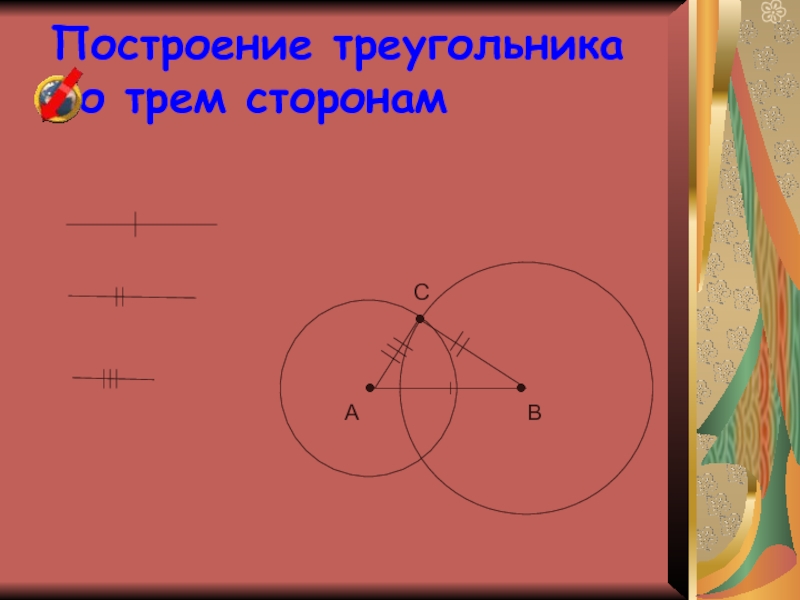
Слайд 29Построение треугольника по трем сторонам
•
•
•
C
B
A
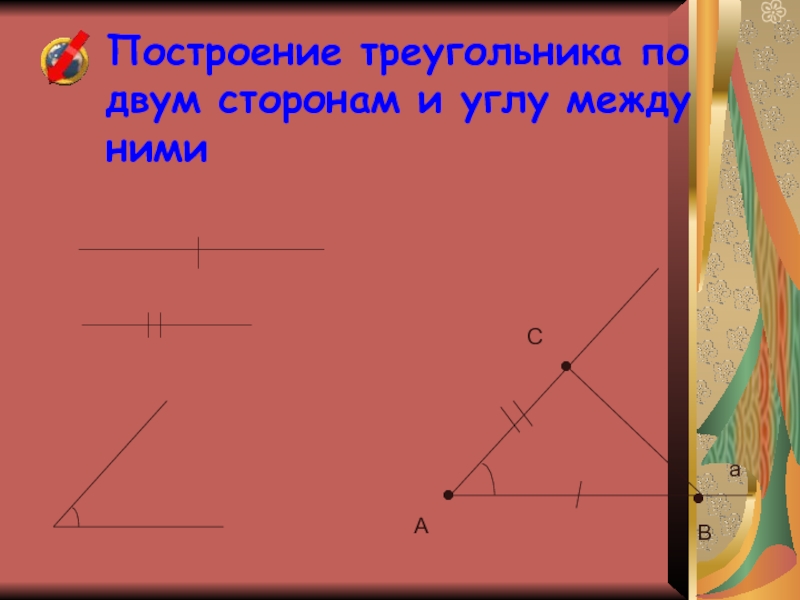
Слайд 30Построение треугольника по двум сторонам и углу между ними
•
•
•
A
B
C
a
Слайд 31Построение треугольника по стороне и прилежащим к ней углам
A
B
C
площади треугольника
Формула Герона)
где r- вписанной
окружности
где
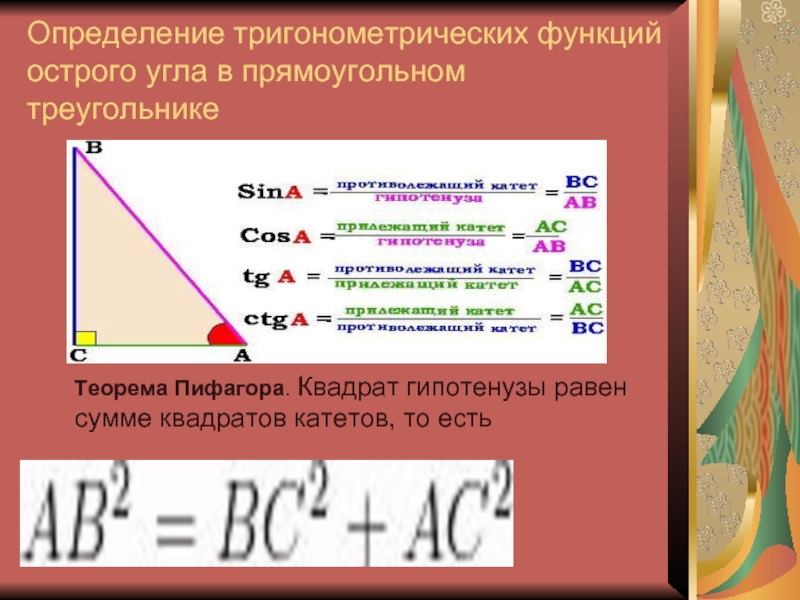
Слайд 34Определение тригонометрических функций острого угла в прямоугольном треугольнике
Теорема Пифагора. Квадрат
гипотенузы равен сумме квадратов катетов, то есть
Слайд 35Определение: два треугольника называются подобными, если у них соответствующие углы
равны и
сходственные стороны пропорциональны, то есть
и
Обозначение:
Подобие треугольников
Слайд 36Признаки подобия двух треугольников
Если два угла одного треугольника
соответственно
равны двум углам другого треугольника,
то такие треугольники подобны.
Если
две стороны одного треугольника пропорциональны
двум сторонам другого треугольника, а углы,
образованные этими сторонами равны,
то треугольники подобны.
Если три стороны одного треугольника
пропорциональны трем сторонам другого треугольника, то треугольники подобны.
Слайд 37Свойство медиан в треугольнике.
1) Все медианы треугольника пересекаются
в одной
точке (центр тяжести треугольника) и делятся этой точкой в отношении
2:1, считая от вершин.
2) Каждая медиана,
проведенная в треугольнике делит этот треугольник
на две равновеликие части (на два треугольника с равными площадями),
то есть
3) Все три медианы делят треугольник
на 6 равновеликих треугольников, то есть
Слайд 38
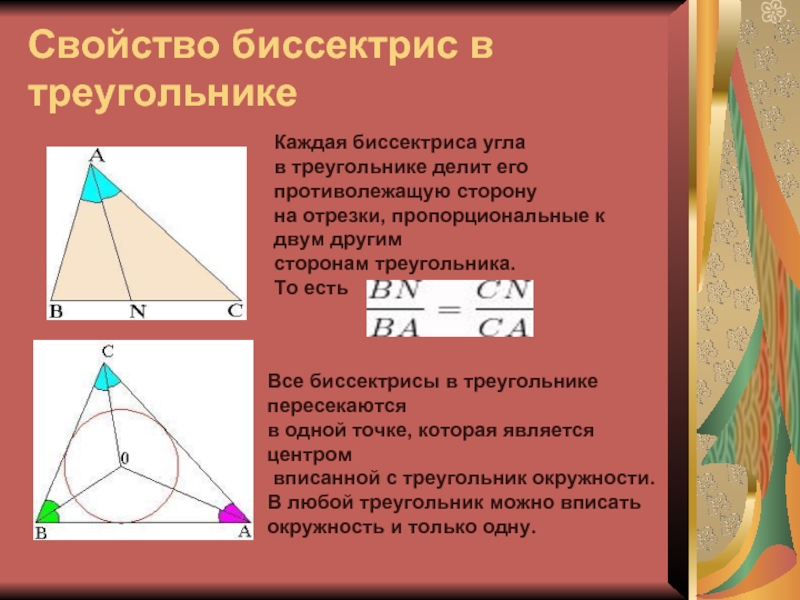
Свойство биссектрис в треугольнике
Каждая биссектриса угла
в треугольнике делит
его противолежащую сторону
на отрезки, пропорциональные к двум другим
сторонам
треугольника.
То есть
Все биссектрисы в треугольнике пересекаются
в одной точке, которая является центром
вписанной с треугольник окружности.
В любой треугольник можно вписать окружность и только одну.
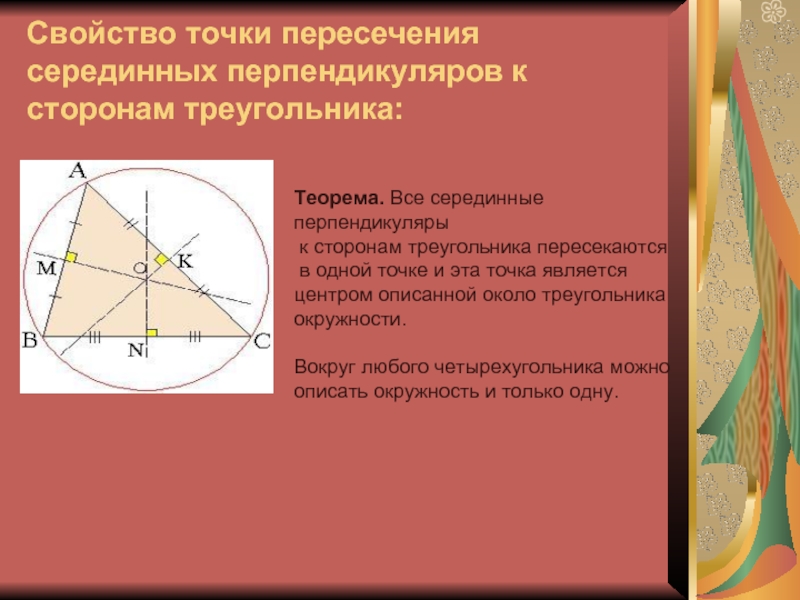
Слайд 39Свойство точки пересечения серединных перпендикуляров к сторонам треугольника:
Теорема. Все серединные
перпендикуляры
к сторонам треугольника пересекаются
в одной точке и эта
точка является
центром описанной около треугольника окружности.
Вокруг любого четырехугольника можно описать окружность и только одну.
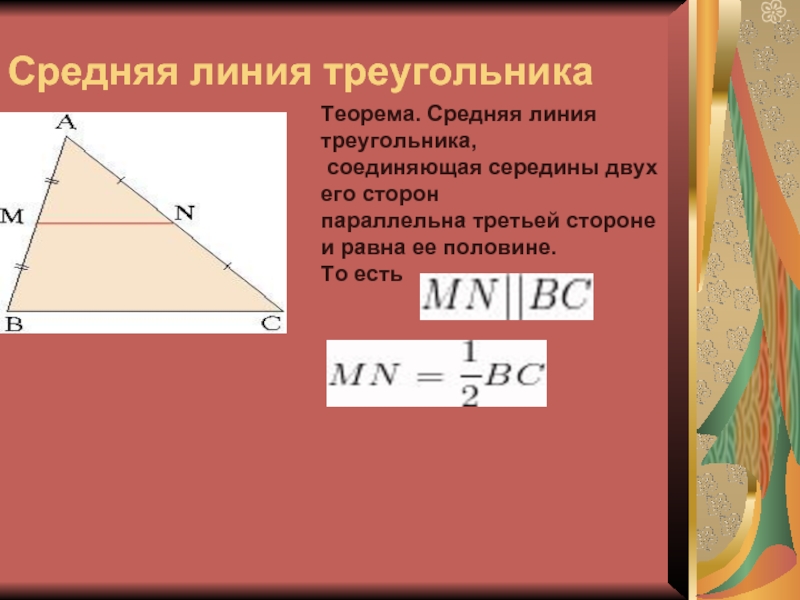
Слайд 40Средняя линия треугольника
Теорема. Средняя линия треугольника,
соединяющая середины двух его
сторон
параллельна третьей стороне и равна ее половине.
То есть
и
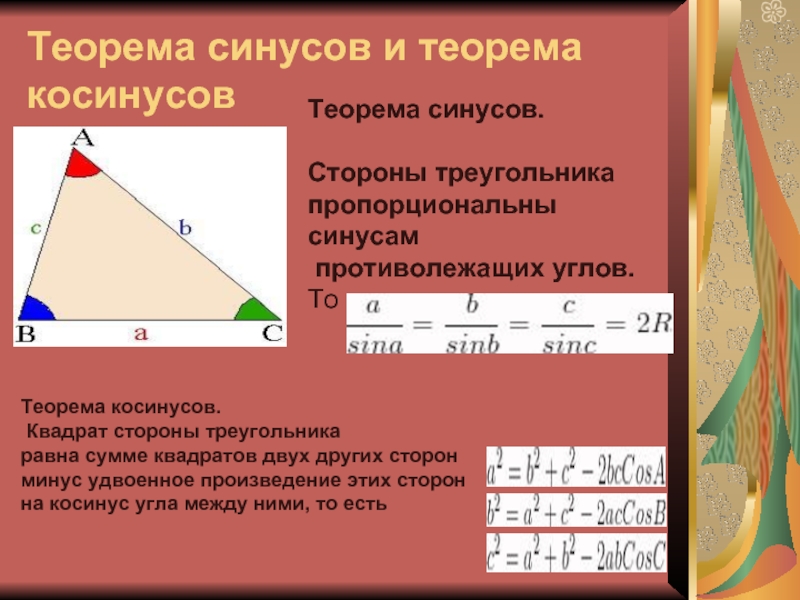
Слайд 41Теорема синусов и теорема косинусов
Теорема синусов.
Cтороны треугольника пропорциональны синусам
противолежащих углов.
То есть
Теорема косинусов.
Квадрат стороны треугольника
равна
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними, то есть
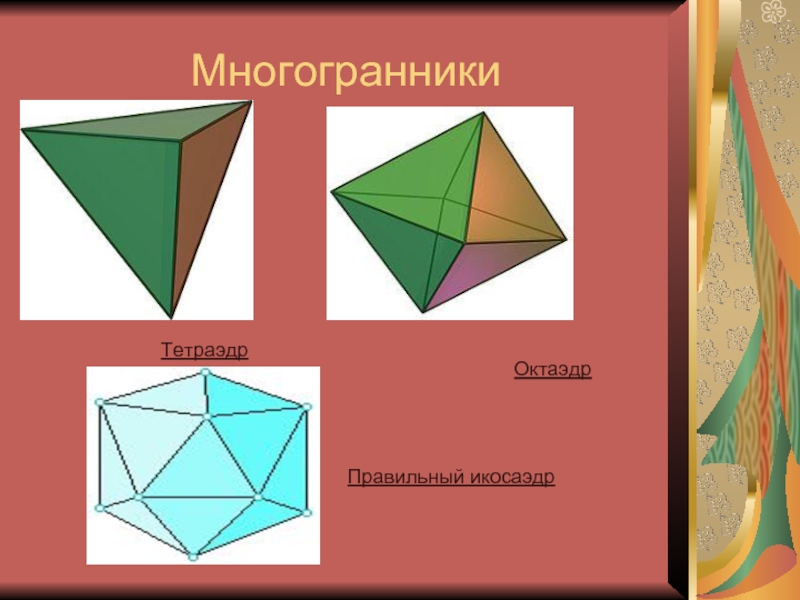
Слайд 42Многогранники
Тетраэдр
Октаэдр
Правильный икосаэдр
Слайд 43Конус
Вращаем прямоугольный треугольник вокруг катета.
Примеры конуса
Слайд 44Треугольники в природе
Одноклеточный организм феодарии (Circjgjniaicosahtdra) no форме напоминает икосаэдр
Многие природные кристаллы
имеют форму октаэдра.
Это алмаз, хлорид натрия,
пероксит,
оливин, флюорит, шпинель.
Слайд 45Бермудский треугольник
Бермудский треугольник — район в Атлантическом океане, в котором
якобы происходят таинственные исчезновения морских и воздушных судов. Район ограничен
линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы. Аналогичный «треугольник» в Тихом океане называют Дьявольским.
Бермудский треугольник — район в Атлантическом океане,
в котором якобы происходят таинственные исчезновения
морских и воздушных судов. Район ограничен линиями
от Флориды к Бермудским островам, далее к Пуэрто-Рико
и назад к Флориде через Багамы. Аналогичный «треугольник»
в Тихом океане называют Дьявольским.
Слайд 46 Треугольник относится к самым маленьким созвездиям. Над горизонтом
наиболее высоко это созвездие находится с октября до марта, .
Около него расположены созвездия Персея, Овна, Рыб и Андромеды. Ясной и безлунной ночью невооруженным глазом в созвездии Треугольника можно видеть около 15 звезд,
Созвездие Треугольник
Слайд 47Треугольник можно увидеть на иконе Богоматери Владимирской.
Геометрические фигуры дидактическим
образом показывают символическую сущность иконы. Это первый священный треугольник Владимирской
Богоматери, с пропорциями 3, 4, 5 и “intimus окружностью”, радиус которой равен 1. Золотой прямоугольник расположен вертикально, и его пропорции равны 2 и 2.
Слайд 48Треугольник Пенроуза или трибар из коллекции невозможных объектов. Кажется, что
мы видим три бруска квадратного сечения соединенных в треугольник. Если
вы закроете любой угол этой фигуры, то увидите, что все три бруска соединены правильно. Но когда вы уберете руку с закрытого угла, то станет очевиден обман. Те два бруска, которые соединятся в этом угле, не должны быть даже вблизи друг друга!
Невозможный треугольник
Слайд 53Гостиница «Золотой треугольник» в Санкт-Петербурге
Слайд 54ТРЕУГОЛЬНИК
Самолёт летит по небу,
Треугольное крыло,
На моём велосипеде,
Треугольное седло,
Есть такой предмет
- угольник,
И всё это - ТРЕУГОЛЬНИК.
Тут мама три спички
На
стол положила
И мне треугольник
Из спичек сложила.
А в это время я чертил
И наблюдал за мамою,
Я три прямых соединил
И сделал то же самое.
Слайд 55
Сколько всего равнобедренных треугольников на чертеже?
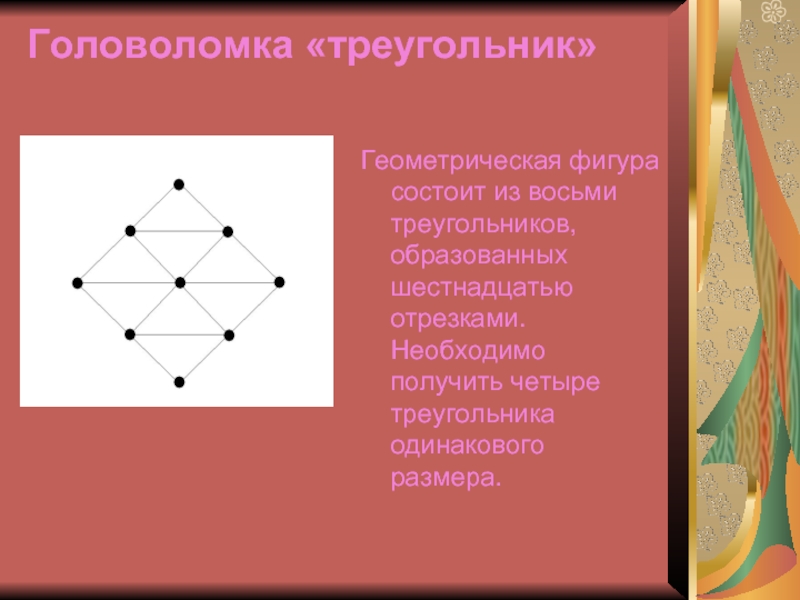
Слайд 56Головоломка «треугольник»
Геометрическая фигура состоит из восьми треугольников, образованных шестнадцатью отрезками.
Необходимо получить четыре треугольника одинакового размера.
Слайд 57Частушки -"запростушки" о треугольнике и его элементах.
Формула Герона
(площадь треугольника
по трем сторонам)
Герон полупериметр
под корень затащил,
Три раза перемножил
и площадь
получил.
Автор этих частушек Ф.С. Веснин, заслуженный рационализатор РСФСР.
Частушки можно найти в книге
"Таблица логарифмов в уме».
Слайд 58Источники:
Савин. А.П.,1985 «Энциклопедия. Словарь юного математика.»
Б.А.Кордемский, А .А
.Ахадов,1986 «Удивительный мир чисел.»
А.В. Спивак “Математический кружок”.
Л.М. Фридман “Изучаем математику”
И.Ф.
Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия»
Атанасян Л.С. «Геометрия 7-9», 2004г., Просвещение
Яндекс «Википедия»
Интернет-ресурсы.