Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЦЕЛЫЕ ЧИСЛА. МЕТОД КООРДИНАТ. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
Содержание
- 1. ЦЕЛЫЕ ЧИСЛА. МЕТОД КООРДИНАТ. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
- 2. ЦЕЛЬ ЗАНЯТИЯИзучить целые числа числа.Ознакомиться с прямоугольной
- 3. ЦЕЛЫЕ ЧИСЛА
- 4. ЦЕЛЫЕ ЧИСЛА 5-2=3; -натуральное число
- 5. СРАВНЕНИЕ ЦЕЛЫХ ЧИСЕЛ1
- 6. ПРАВИЛА СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ
- 7. ПРАВИЛА СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ
- 8. МЕТОД КООРДИНАТ. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
- 9. ОПРЕДЕЛЕНИЕ КООРДИНАТЫ Координаты— это набор данных, по которому определяется положение того или иного объекта.
- 10. ДЕКАРТОВА СИСТЕМА КООРДИНАТФранцузский математик Рене Декарт
- 11. СИСТЕМА КООРДИНАТСистема координат —это две взаимно перпендикулярные координатные
- 12. СИСТЕМА КООРДИНАТПрямоугольная система координат — прямолинейная система координат с
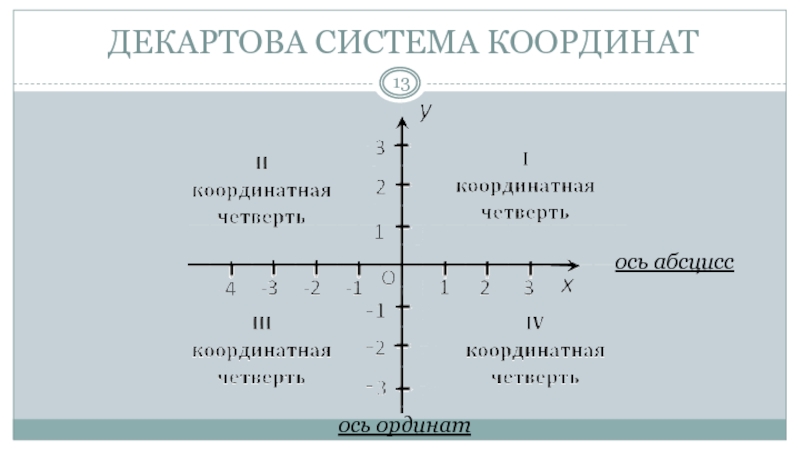
- 13. ДЕКАРТОВА СИСТЕМА КООРДИНАТось абсциссось ординат
- 14. ДЕКАРТОВА СИСТЕМА КООРДИНАТКак найти положение точки
- 15. ДЕКАРТОВА СИСТЕМА КООРДИНАТКак найти положение точки
- 16. ДЕКАРТОВА СИСТЕМА КООРДИНАТРасшифровать фразу : «Лучше один раз увидеть, чем сто раз услышать»
- 17. КАКОЕ ЖИВОТНОЕ ЗАШИФРОВАНО?Туловище: (-6;-1), (-5;-4), (-2;-6), (-1;-4),
- 18. Скачать презентанцию
ЦЕЛЬ ЗАНЯТИЯИзучить целые числа числа.Ознакомиться с прямоугольной системой координат.Определять координаты точки, отмеченной на координатной плоскости.Научиться строить точки по заданным её координатам.
Слайды и текст этой презентации
Слайд 1Введение В ПРОГРАММИРОВАНИЕ ДЛЯ НАЧИНАЮЩИХ
ЦЕЛЫЕ ЧИСЛА. МЕТОД КООРДИНАТ. ПРЯМОУГОЛЬНАЯ СИСТЕМА
КООРДИНАТ НА ПЛОСКОСТИ
Слайд 2ЦЕЛЬ ЗАНЯТИЯ
Изучить целые числа числа.
Ознакомиться с прямоугольной системой координат.
Определять координаты
точки, отмеченной на координатной плоскости.
Научиться строить точки по заданным её
координатам.Слайд 4ЦЕЛЫЕ ЧИСЛА
5-2=3; -натуральное число
2-5=-
3; - отрицательное числоа, -а - противоположные числа
Между натуральными и отрицательными числами находится число «0»
а+0=а; а+(-а)=0;
N- множество натуральных чисел
Z- множество целых чисел
Слайд 5СРАВНЕНИЕ ЦЕЛЫХ ЧИСЕЛ
1
лежит на числовой прямой левее другого.
| | - абсолютная величина.
|а|=а
|-а|=а |0|=0Отрицательное число меньше «0».
«0» меньше положительного числа.
Из двух отрицательных чисел меньше то, у которого больше отрицательная величина.
-5<0 -10<-5 -5<3
Слайд 6ПРАВИЛА СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ И ДЕЛЕНИЯ
При
сложении двух положительных или двух отрицательных чисел, складывают их абсолютные
величины и приписывают сумме тот же знак.2+5=7 -2 + (-5)= -7
При сложении чисел с разными знаками, от большей абсолютной величины отнимают меньшую приписывают сумме знак числа большей абсолютной величины.
-5+3=-2 5+(-3)=2
Вычитание можно заменить сложением
-5-3= -5+(-3)= -8 3-5=3+(-5)=-2 3-(-5)=8
Слайд 7ПРАВИЛА СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ И ДЕЛЕНИЯ
Произведение
и частное двух чисел с одинаковыми знаками положительно.
Произведение и частное
двух чисел с разными знаками отрицательно.(-2)*(-2)= 4 (-4):(-2)= 2
(-2)* 3=- 6 (-4): 2= -2
Слайд 9ОПРЕДЕЛЕНИЕ КООРДИНАТЫ
Координаты— это набор данных, по которому определяется положение
того или иного объекта.
Слайд 10 ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Французский математик Рене Декарт (1596–1650) предложил задавать
положение точки на плоскости с помощью двух координат.
Слайд 11СИСТЕМА КООРДИНАТ
Система координат —это две взаимно перпендикулярные координатные прямые, пересекающиеся в
точке, которая является началом отсчёта для каждой из них. Совокупность чисел,
определяющих положение конкретной точки, называется координатамиэтой точки.
Слайд 12СИСТЕМА КООРДИНАТ
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями
на плоскости или в пространстве.
Декартовой обычно называют прямоугольную систему координат с одинаковыми
масштабами по осям.Слайд 14 ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Как найти положение точки по её координатам?
Найти
точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение
точки по её координатам, например, точки D (−4 , 2), надо:Отметить на оси Ox, точку с координатой (−4), и провести через неё прямую перпендикулярную оси 0x.
Отметить на оси Oy, точку с координатой (2), и провести через неё прямую перпендикулярную оси 0y.
Точка пересечения перпендикуляров (·) D — искомая точка. У неё абсцисса равна (−4), а ордината равна (2).
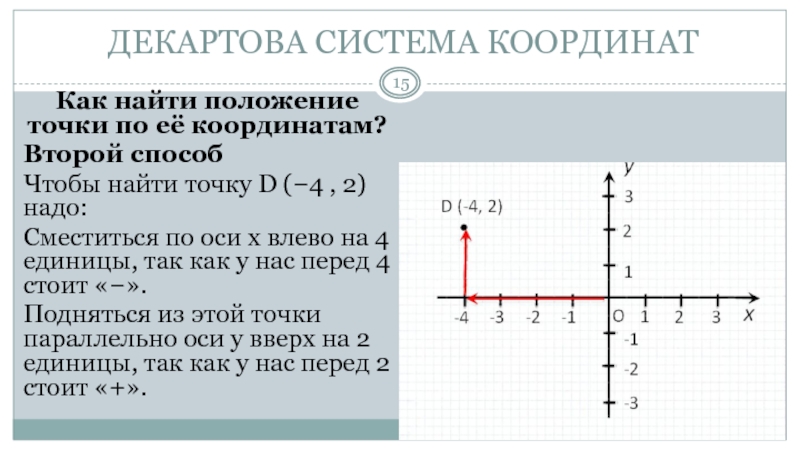
Слайд 15 ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Как найти положение точки по её координатам?
Второй
способ
Чтобы найти точку D (−4 , 2) надо:
Сместиться по оси
x влево на 4 единицы, так как у нас перед 4 стоит «−».Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».
Слайд 16 ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Расшифровать фразу :
«Лучше один раз увидеть,
чем сто раз услышать»
Слайд 17КАКОЕ ЖИВОТНОЕ ЗАШИФРОВАНО?
Туловище:
(-6;-1), (-5;-4), (-2;-6), (-1;-4), (0;-5), (1;-5), (3;-7),
(2;-8), (0;-8), (0;-9), (3;-9),(4;-8), (4;-4), (5;-6), (8;-4), (8;0), (6;2), (4;1),
(0;1), (-2;2), (-6;-1), (-10;-2), (-13;-4), (-14;-7), (-16;-9),(-13;-7), (-12;-10), (-13;-14),(-10;-14), (-10;-13), (-9;-13), (-10;-9), (-5;-9),(-5;-15), (-2;-15),(-2;-13). (-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11), (2;-9)Глаза: (0;-2) и (4;-2)