Управляющие процессы и их формализованное описание

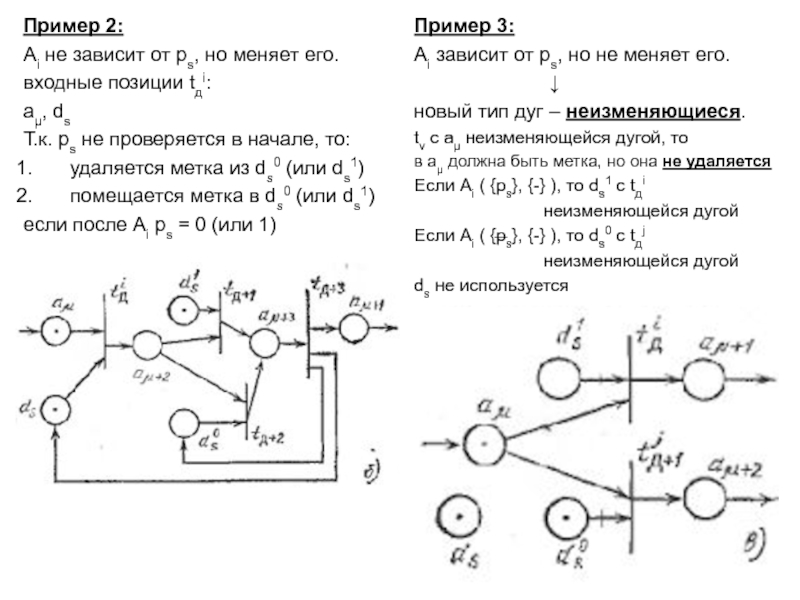
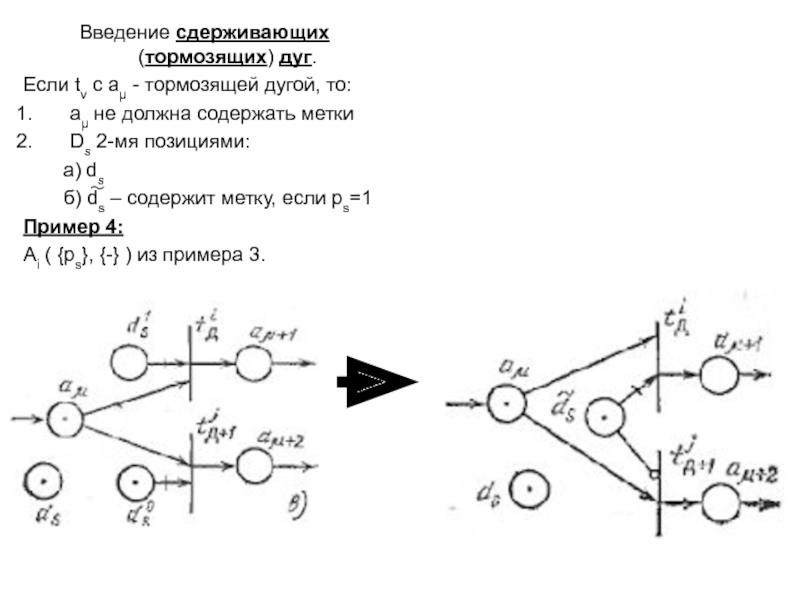
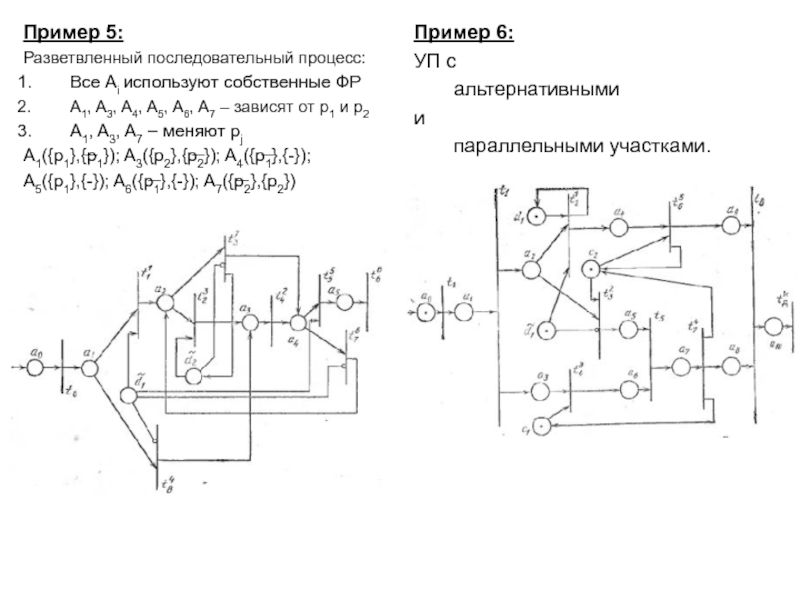
– ЛР
в ЛР Ds проверяется ps – условие
Внутренние ЛР
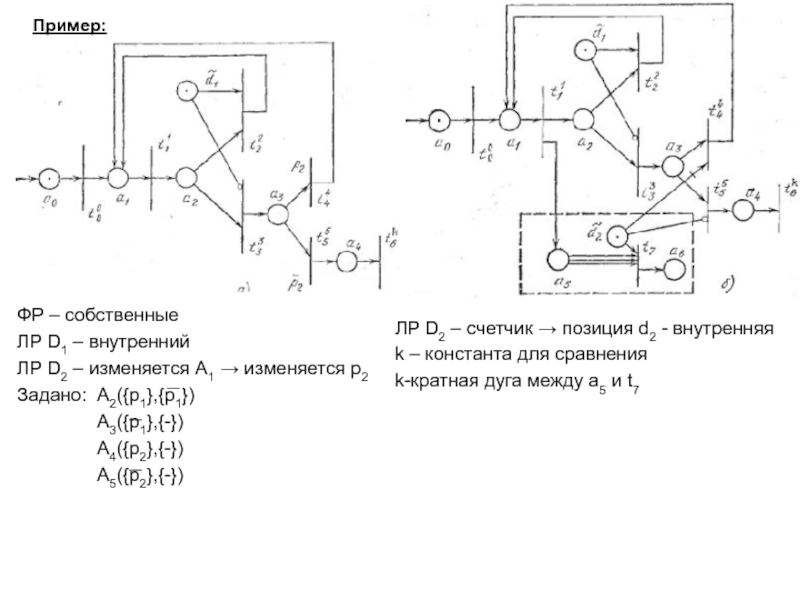
Ai (

{P1i}, {P2i} )
Пример:
Ai ( {p1, p2}, {p2, p3} )
ps – {P2i} – изменяется Ai → Ds – занято
ps – {P1i} – не изменяется Ai → Ds – не занято
Описание ЛР в сети Петри.
ds – наличие метки – нет монополии
Ds ds1 – наличие метки – ps = 1
ds0 – наличие метки – ps = 0
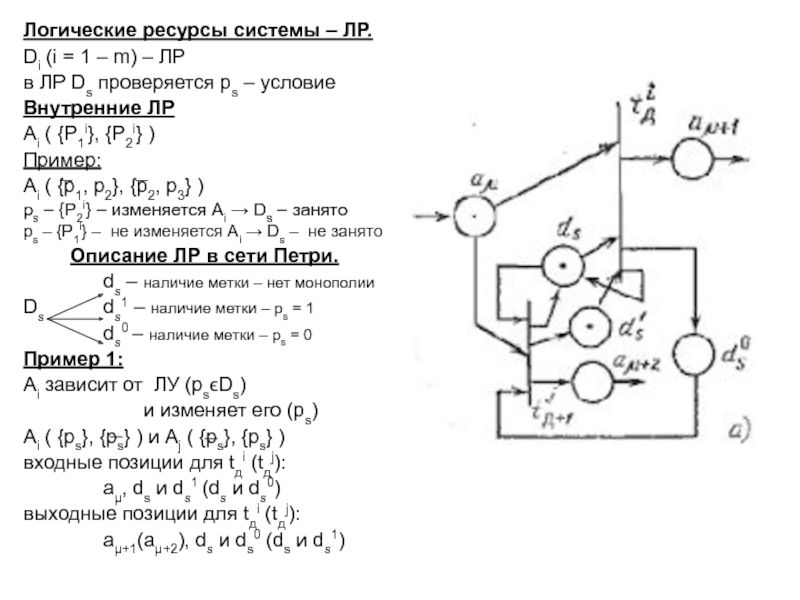
Пример 1:
Ai зависит от ЛУ (psϵDs)
и изменяет его (ps)
Ai ( {ps}, {ps} ) и Aj ( {ps}, {ps} )
входные позиции для tдi (tдj):
aµ, ds и ds1 (ds и ds0)
выходные позиции для tдi (tдj):
aµ+1(aµ+2), ds и ds0 (ds и ds1)

tдi:
aµ, ds
Т.к. ps не проверяется в начале, то:
удаляется метка из

ds0 (или ds1)
помещается метка в ds0 (или ds1)
если после Ai ps = 0 (или 1)

Пример 3:
Ai зависит от ps, но не меняет его.
↓
новый тип дуг – неизменяющиеся.
tv c aµ неизменяющейся дугой, то
в aµ должна быть метка, но она не удаляется
Если Ai ( {ps}, {-} ), то ds1 c tдi
неизменяющейся дугой
Если Ai ( {ps}, {-} ), то ds0 c tдj
неизменяющейся дугой
ds не используется

то:
aµ не должна содержать метки
Ds 2-мя позициями:
а) ds
б) ds –

содержит метку, если ps=1
Пример 4:
Ai ( {ps}, {-} ) из примера 3.

A5, A6, A7 – зависят от p1 и p2
A1, A3,

A7 – меняют pj
A1({p1},{p1}); A3({p2},{p2}); A4({p1},{-});
A5({p1},{-}); A6({p1},{-}); A7({p2},{p2})

Пример 6:
УП с
альтернативными
и
параллельными участками.

hu – метка есть, если pu=1; нет при pu=0
внеш. ЛУ

ϵ {P1}
есть внутренние и внешние ЛУ
если Ai выполняется при pu=1 (0), то hu соединяется с tдi сдерживающей дугой
не включается позиция состояния внешнего ЛР
развитие процесса – зависит от начальной маркировки внутренних позиций и текущей маркировки внешних входных позиций
замена внешних входных позиций на предикаты, зависящие от внешних ЛУ

Если не определено влияние Ai на значение ps:
возможное изменение ps – это безразличное значение (ps) в {P2i}
позиция состояния Ds - в описании параллельного процесса
на время выполнения tдi метка из ds удаляется
позиция ds аналогична внешней позиции

→ изменяется p2
Задано: A2({p1},{p1})
A3({p1},{-})
A4({p2},{-})
A5({p2},{-})
ЛР D2 – счетчик → позиция d2 -

внутренняя
k – константа для сравнения
k-кратная дуга между a5 и t7