Уравнение вихря скорости

качественной оценки изменений давления со временем в данном районе. Впервые

такое наглядное представление с применением натуральной системы координат было предложено В.А. Бугаевым.

Государственной (1948, за исследования в области физики атмосферы; 1971, за участие

в создании Атласа Антарктики, в составе авторского коллектива) и Ленинской премий (1974, за большой научный вклад в развитие метеорологии и разработку плана Всемирной службы погоды, за большой вклад в развитие гидрометеослужбы в СССР). Награждён орденом Ленина, двумя орденами Красного Знамени и рядом медалей.

то можем записать:

или

изменениями барического поля во времени:
Для циклонической завихренности:


Для

антициклонической завихренности:

имеет волновую структуру, то для каждой элементарной волны в первом

приближении имеем:

v и Ω подставим выражения в геострофическом приближении:

по касательной к изогипсе, ось n направлена в сторону возрастающих

значений H, т.е. совпадает с осью Y, но противоположно направлена.
Тогда

наклона изогипсы H к оси S

, равна нулю.

В случае криволинейных изогипс

которой в дифференциальной геометрии получена формула



Выразим производные .
Поскольку

H(x,y)=const – неявно заданная кривая, т.е. мы не знаем вида функции y=f(x),найдём

и при условии, что

производную повторно продифференцировав полученное выражение с учётом того, что все

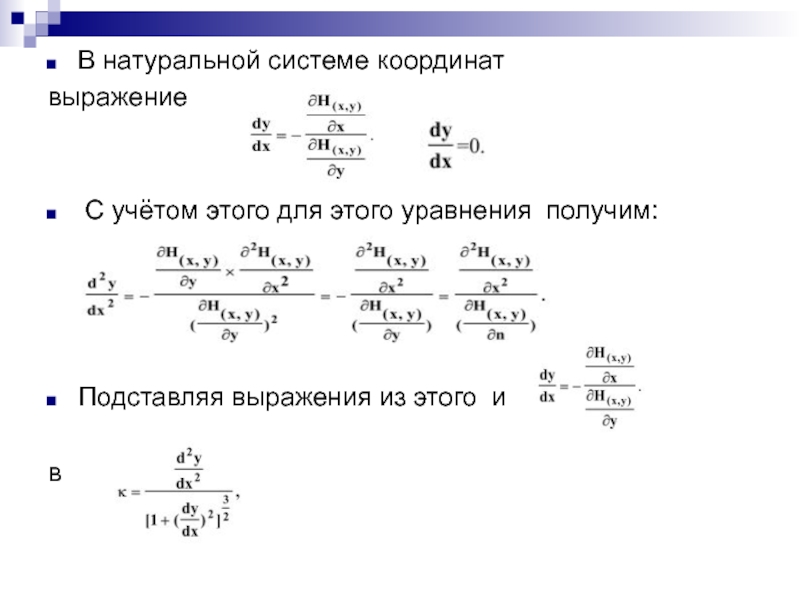
частные производные в правой части зависят и от x и от y, при этом y=f(x):

этого уравнения получим:




Подставляя выражения из этого и

в

системе координат имеем:



или, следуя общепринятым обозначениям для натуральной системы, получим

уравнение Бугаева:

при увеличении антициклонического вихря, т.е. при отрицательной адвекции вихря:

Hn

>0, поскольку n направлена в сторону возрастающих значений H.
H ns – изменение вдоль потока S: >0 при сходимости изогипс, <0
при расходимости изогипс.
κ – кривизна изогипс: к >0 при циклонической кривизне изогипс, к<0 при антициклонической кривизне изогипс.
– изменение кривизны по потоку: >0 – при увеличении циклонической кривизны изогипс или уменьшении антициклонической; ; <0 – при уменьшении циклонической кривизны изогипс или увеличении антициклонической.
H nns – изменение градиента геопотенциала вдоль потока и и по нормали к изогипсам (вклад данного слагаемого невелик, обычно не рассматривается).

общей качественной оценки изменения барического поля в данном районе.Практический опыт

синоптика показывает, что наиболее благоприятные условия для развития циклона складываются, когда приземный центр его располагается под передней частью высотной барической ложбины на АТ 500, где, при наличии значительных горизонтальных градиентов геопотенциала(высотная фронтальная зона), наблюдается уменьшение циклонической кривизны по потоку.Усиливающим эффектом является циклоническая кривизна изогипс при их расходимости по потоку.

его располагается под тыловой частью высотной барической ложбины на АТ

500 , где, при наличии значительных горизонтальных градиентов геопотенциала (высотная фронтальная зона), наблюдается увеличение циклонической кривизны по потоку. Усиливающим эффектом является циклоническая кривизна изогипс при их сходимости по потоку.