TheSlide.ru

Уравнения Максвелла Уравнения Максвелла Электростатика Электродинамика – сила

Содержание

1. Уравнения Максвелла Уравнения Максвелла Электростатика Электродинамика – сила
2. Уравнения МаксвеллаУравнения МаксвеллаВещество изменяет внешнее поле, так
3. Уравнения МаксвеллаЗакон сохранения энергии электромагнитного поля. Поток
4. Уравнения МаксвеллаЗакон сохранения энергии электромагнитного поля. Поток энергии.– плотность электромагнитной энергии– вектор Пойтинга (плотность потока энергии)
5. Уравнения МаксвеллаЗаконы преобразования E и BПреобразования ЛоренцаИз законов преобразования силы
6. Уравнения МаксвеллаИнварианты электромагнитного поляИз формул преобразования Следствие 1.
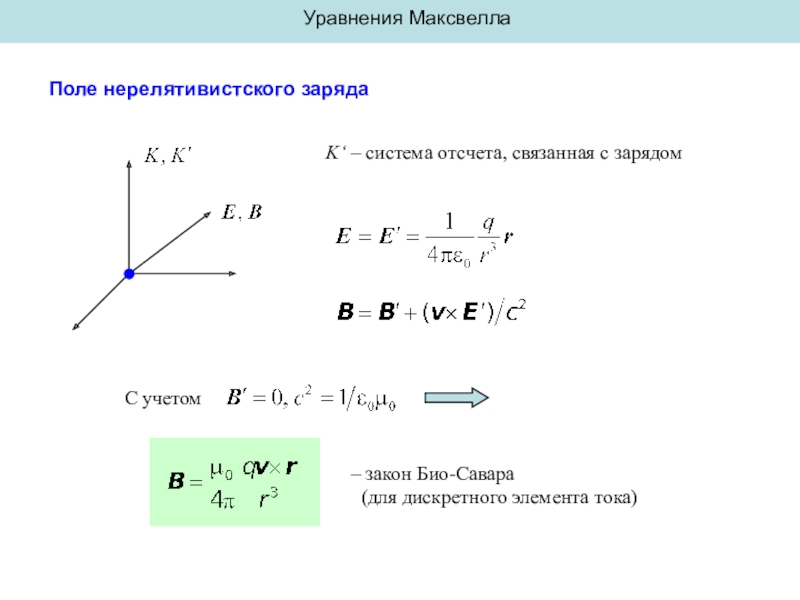
7. Уравнения МаксвеллаПоле нерелятивистского зарядаK‘ – система отсчета,
8. Уравнения МаксвеллаПреобразование зарядов и токовФормулы преобразования зарядов и токов
9. Скачать презентанцию

Уравнения МаксвеллаУравнения МаксвеллаВещество изменяет внешнее поле, так как поле вещество поляризует и намагничивает.– уравнения Максвелла в среде– материальные уравнения– граничные условия

Главная
Разное
Уравнения Максвелла Уравнения Максвелла Электростатика Электродинамика – сила

Слайды и текст этой презентации

Слайд 1Уравнения Максвелла
Уравнения Максвелла
Электростатика
Электродинамика
– сила Лоренца
– уравнения Максвелла (в вакууме)
–

закон Кулона (полевая форма)

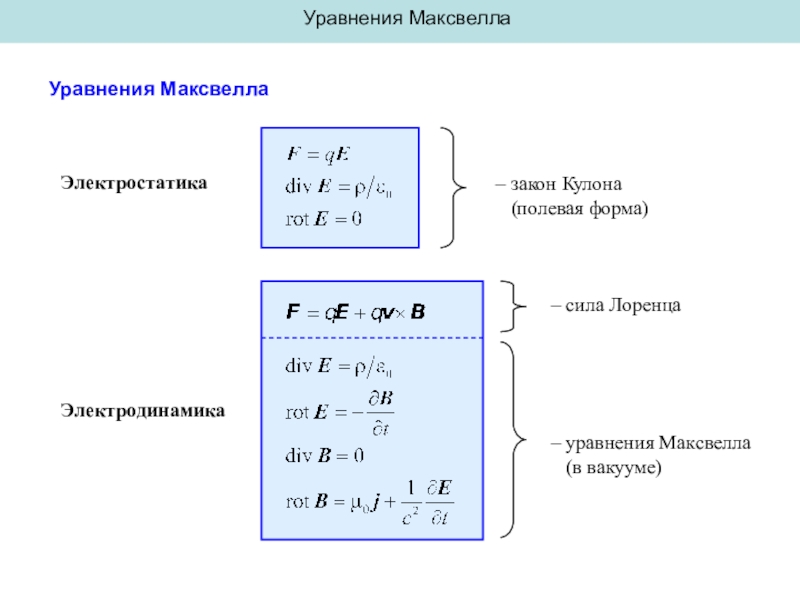
Уравнения МаксвеллаУравнения МаксвеллаЭлектростатикаЭлектродинамика– сила Лоренца– уравнения Максвелла (в вакууме)– закон Кулона (полевая форма)

Слайд 2Уравнения Максвелла
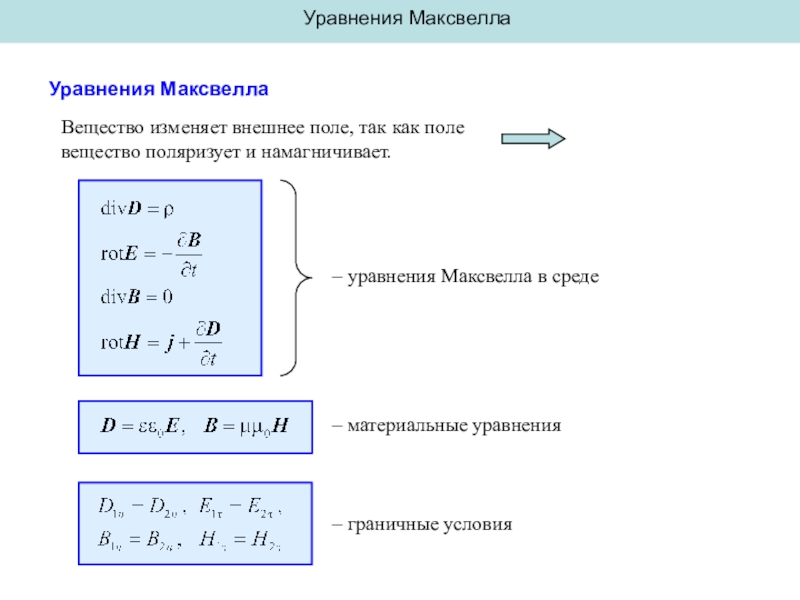
Уравнения Максвелла
Вещество изменяет внешнее поле, так как поле вещество поляризует

и намагничивает.
– уравнения Максвелла в среде
– материальные уравнения
– граничные условия

Уравнения МаксвеллаУравнения МаксвеллаВещество изменяет внешнее поле, так как поле вещество поляризует и намагничивает.– уравнения Максвелла в среде–

Слайд 3Уравнения Максвелла
Закон сохранения энергии электромагнитного поля. Поток энергии.
Мощность, развиваемая действующими на

ток силами электромагнитного поля
. . . . .

Уравнения МаксвеллаЗакон сохранения энергии электромагнитного поля. Поток энергии.Мощность, развиваемая действующими на ток силами электромагнитного поля. . .

Слайд 4Уравнения Максвелла
Закон сохранения энергии электромагнитного поля. Поток энергии.
– плотность электромагнитной энергии
–

вектор Пойтинга (плотность потока энергии)

Уравнения МаксвеллаЗакон сохранения энергии электромагнитного поля. Поток энергии.– плотность электромагнитной энергии– вектор Пойтинга (плотность потока энергии)

Слайд 5Уравнения Максвелла
Законы преобразования E и B
Преобразования Лоренца
Из законов преобразования силы

Уравнения МаксвеллаЗаконы преобразования E и BПреобразования ЛоренцаИз законов преобразования силы

Слайд 6Уравнения Максвелла
Инварианты электромагнитного поля
Из формул преобразования
Следствие 1. Если E  B (т.е.

EB  0) в одной ИСО,

то E'  B' (т.е. E'B'  0) во всех ИСО.

Следствие 2. Если E = cB (т.е. E2 – c2B2  0) в одной ИСО, то E' = cB' (т.е. E'2 – c2B'2  0) во всех ИСО.

Уравнения МаксвеллаИнварианты электромагнитного поляИз формул преобразования Следствие 1. Если E  B (т.е. EB  0) в одной ИСО,

Слайд 7Уравнения Максвелла
Поле нерелятивистского заряда
K‘ – система отсчета, связанная с зарядом
С

учетом
– закон Био-Савара (для дискретного элемента тока)

Уравнения МаксвеллаПоле нерелятивистского зарядаK‘ – система отсчета, связанная с зарядомС учетом– закон Био-Савара (для дискретного элемента

Слайд 8Уравнения Максвелла
Преобразование зарядов и токов
Формулы преобразования зарядов и токов

Уравнения МаксвеллаПреобразование зарядов и токовФормулы преобразования зарядов и токов

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей