Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнения математической физики
Содержание
- 1. Уравнения математической физики
- 2. 08/13/2019Поля физических величинЛюбое физическое явление или процесс
- 3. 08/13/2019Математическая модель поляМатематической моделью поля является функция
- 4. 08/13/2019Прямая полевая задачаЗадано поле
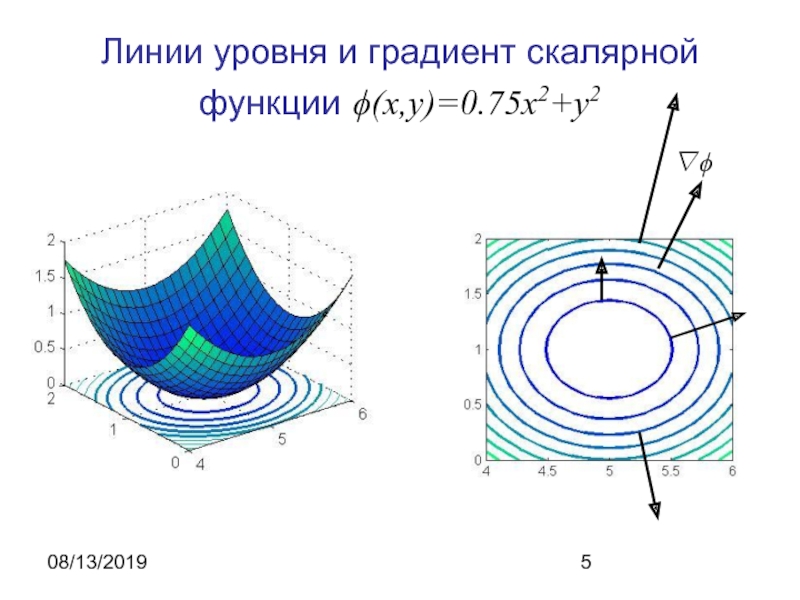
- 5. 08/13/2019Линии уровня и градиент скалярной функции ϕ(x,y)=0.75x2+y2∇ϕ
- 6. 08/13/2019Градиент скалярной функцииХарактеризует направление наибольшего возрастания функции в каждой точке поля.
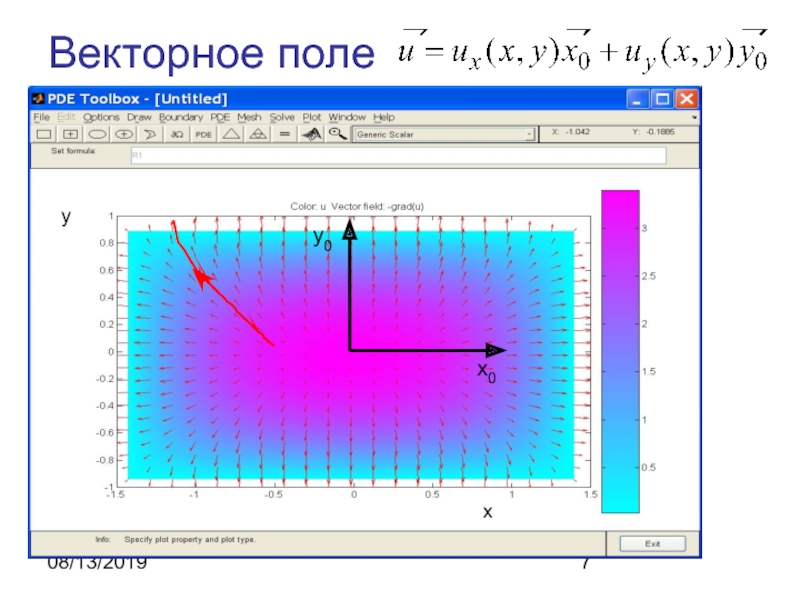
- 7. 08/13/2019Векторное поле xyx0y0
- 8. 08/13/2019Дивергенция векторного поляХарактеризует распределение в пространстве источников
- 9. 08/13/2019Ротор векторного поляХарактеризует завихрения векторного поля.Например известно,
- 10. 08/13/2019Лапласиан от скалярного поляХарактеризует распределение источников скалярного
- 11. 08/13/2019Классификация полей Соленоидальные (или вихревые)
- 12. 08/13/2019Интегральные теоремы Теорема Остроградского – Гаусса:Теорема Стокса:
- 13. 08/13/2019Интегральные теоремы Теорема Грина:Формула интегрирования по частямЕсли Ω=V то Г =S; если Ω=S то Г=линия
- 14. 08/13/2019Обратная полевая задачаИзвестны условия, в которых находится
- 15. 08/13/2019уравнения математической физикиМетоды составления и, главное, решения
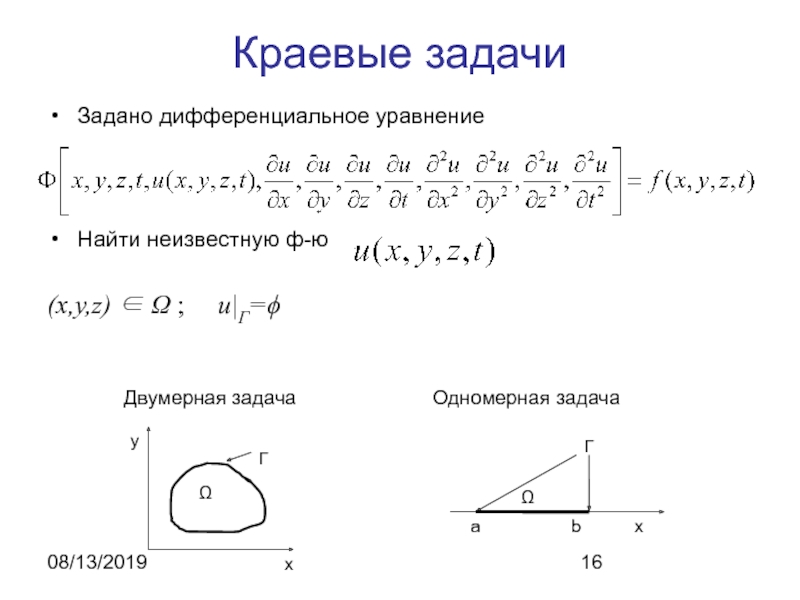
- 16. 08/13/2019Краевые задачиЗадано дифференциальное уравнениеНайти неизвестную ф-ю(x,y,z) ∈ Ω ; u|Г=ϕОдномерная задачаДвумерная задача
- 17. 08/13/2019Конец темы
- 18. Скачать презентанцию
08/13/2019Поля физических величинЛюбое физическое явление или процесс представляет собой распределение и изменение каких-либо физических величин (скалярных, векторных, тензорных) в некоторой области пространства и во времени. Распределение некоторой величины в пространстве и
Слайды и текст этой презентации
Слайд 108/13/2019
Тема 2.
Уравнения математической физики
Поля физических величин
Математическая модель поля
Прямая
полевая задача
Слайд 208/13/2019
Поля физических величин
Любое физическое явление или процесс представляет собой распределение
и изменение каких-либо физических величин (скалярных, векторных, тензорных) в некоторой
области пространства и во времени.Распределение некоторой величины в пространстве и во времени получило название поле.
Такие поля окружают нас -температурное поле, электромагнитное поле, поле скоростей, поле вероятности.
Основной задачей теоретической физики, а так же многих технических приложений является исследование полей физических величин, (полевые задачи).
Для их исследования разработано огромное программное обеспечение.
Слайд 308/13/2019
Математическая модель поля
Математической моделью поля является функция нескольких переменных, обычно
Поля
бывают
скалярные
векторные
Тензорные (т.е.описывается несколькими векторами).
стационарные
Нестационарные
При исследовании полей выделяют две
задачи – прямую и обратную
Слайд 408/13/2019
Прямая полевая задача
Задано поле
;
требуется установить характер этого поля, например быстроту его изменения от точки к точке.Математическая теория поля занимается изучением дифференциальных и интегральных свойств различных полей.
Здесь для векторной
и скалярной
функций введены операторы дифференцирования:
Слайд 608/13/2019
Градиент скалярной функции
Характеризует направление наибольшего возрастания функции в каждой точке
поля.
Слайд 808/13/2019
Дивергенция векторного поля
Характеризует распределение в пространстве источников векторного поля
Например, источниками
электрического поля являются
заряды, положительные или отрицательные.В этом случае дает распределение зарядов.
Слайд 908/13/2019
Ротор векторного поля
Характеризует завихрения векторного поля.
Например известно, что при течении
тока вокруг него образуется вихревое магнитное поле. Так вот, если
мы знаем распределение магнитного полятогда ротор от него дает распределение токов.
Слайд 1008/13/2019
Лапласиан от скалярного поля
Характеризует распределение источников скалярного поля
Например имеется распределение
температуры вдоль плоской пластины T(x,y).
Градиент температуры указывает направление максимального распространения
тепла в данной точкеТогда
дает распределение мощности источников тепла
Зная распределение источников можно получить распределение температуры из уравнения:
Слайд 1108/13/2019
Классификация полей
Соленоидальные (или вихревые)
,
(все силовые линии замкнуты)
такое
поле может быть представлено в виде здесь векторный потенциал.
Потенциальные (или безвихревые) ,
такое поле может быть представлено в виде
здесь скалярный потенциал.
Слайд 1308/13/2019
Интегральные теоремы
Теорема Грина:
Формула интегрирования по частям
Если Ω=V то Г
=S; если Ω=S то Г=линия
Слайд 1408/13/2019
Обратная полевая задача
Известны условия, в которых находится физический объект
требуется найти распределение в пространстве некоторой физической величины, т.е.
конкретного вида математического поля.Чаще всего задача нахождения поля, удовлетворяющего требуемым условиям, приводит к решению краевой задачи для дифференциального (или интегрального) уравнения.
Слайд 1508/13/2019
уравнения математической физики
Методы составления и, главное, решения уравнений такого рода
изучаются в разделе математической физики – теория дифференциальных уравнений в
частных производных и теория интегральных уравнений. Эти уравнения исторически получили название «уравнения математической физики».Совокупность теории поля и теории дифференциальных уравнений в частных производных образует так называемую классическую математическую физику.
Основной метод решения - проекционно-сеточный метод, который получил название метод конечных элементов
Слайд 1608/13/2019
Краевые задачи
Задано дифференциальное уравнение
Найти неизвестную ф-ю
(x,y,z) ∈ Ω ;
u|Г=ϕ
Одномерная задача
Двумерная задача
