Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок математики по теме: Десятичные и натуральные логарифмы. Формула перехода
Содержание
- 1. Урок математики по теме: Десятичные и натуральные логарифмы. Формула перехода
- 2. Цели урока.Повторить свойства логарифмовРешать задачиРешать уравненияВвести понятия натурального и десятичного логарифмов
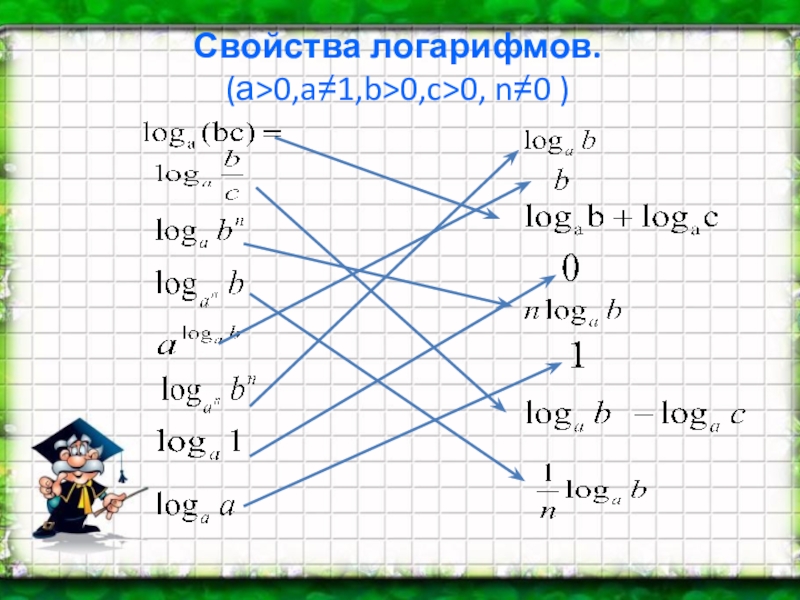
- 3. Свойства логарифмов. (а>0,a1,b>0,c>0, n0 ):
- 4. Найдите значение выражений4- 0,5 -0,543932511-22
- 5. Решите уравнение
- 6. Сравните ответы
- 7. Тренировочный тест1.Вычислить: 0,3log0,32 – 5– 4,91;
- 8. Проблема Обратите внимание - действия с
- 9. Десятичным логарифмом называется логарифм по основанию 10.
- 10. Переход к другому основаниюТеорема Пусть дан логарифм
- 11. Воспользуемся сначала свойствомТеперь перейдем к основанию 2
- 12. 2) Найдите значение выражения
- 13. 3)Найдите значение выражения , если Решение:Решение:Ответ: 12
- 14. Спасибо за урок.
- 15. Скачать презентанцию
Цели урока.Повторить свойства логарифмовРешать задачиРешать уравненияВвести понятия натурального и десятичного логарифмов
Слайды и текст этой презентации
Слайд 1
Урок математики по теме:
«Десятичные и натуральные логарифмы.
Формула перехода к
другому основанию»
Слайд 2Цели урока.
Повторить свойства логарифмов
Решать задачи
Решать уравнения
Ввести понятия натурального и десятичного
логарифмов
Слайд 7Тренировочный тест
1.Вычислить: 0,3log0,32 – 5
– 4,91;
2) – 4,7; 3) – 3;
4) 2.2. Найдите значение выражения: log216 + log22
1) 4; 2) 5; 3) 6; 4) 4,5.
3.Найдите значение выражения : log0,39 -2log0,310
1) 2; 2) 1; 3) – 2; 4) 90.
4. Найдите x : lgx = 1/2lg9 – 2/3lg8
1) 3/4; 2) 4/3; 3) 3/2; 4) 6.
5. Упростите выражение: 32+log315
1) 17; 2) 135; 3) 225; 4) 30.
Слайд 8Проблема
Обратите внимание - действия с логарифмами возможны только
при одинаковых основаниях! А если основания разные!?
Слайд 9Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg
, т.е. log 10 m = lg т
Натуральным логарифмом
называется логарифм по основанию е. Он обозначается ln , т.е. log e m = ln m. Число е является иррациональным, его приближённое значение 2.718281828.Слайд 10Переход к другому основанию
Теорема
Пусть дан логарифм loga b. Тогда
для любого числа c такого, что c > 0 и c ≠
1, верно равенство:В частности, если положить c = b, получим: