Переходные процессы в цепях второго порядка

постоянное напряжение. Апериодический процесс. Критический процесс. Колебательный процесс. Операторный

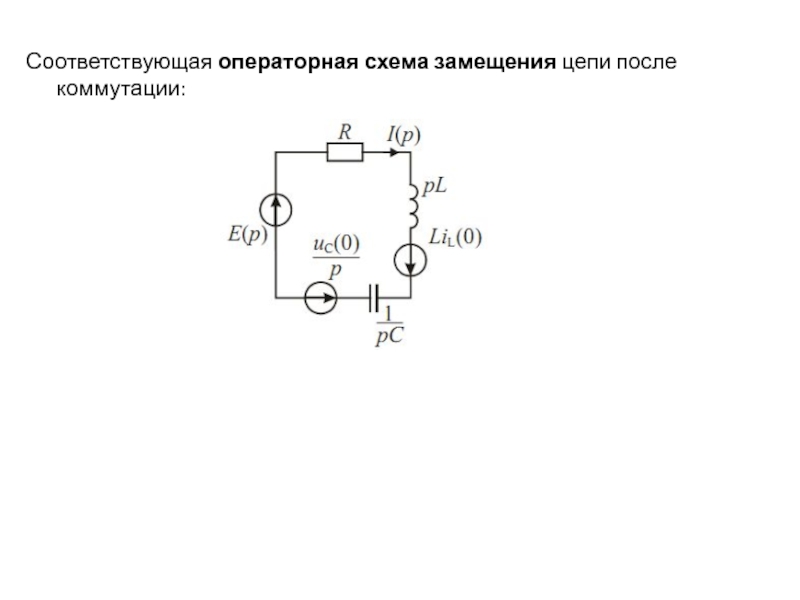
При наличие двух независимых накопителей энергии переходные процессы в них описываются уравнениями второго порядка. Простейший пример такой цепи – последовательное соединение RLC.
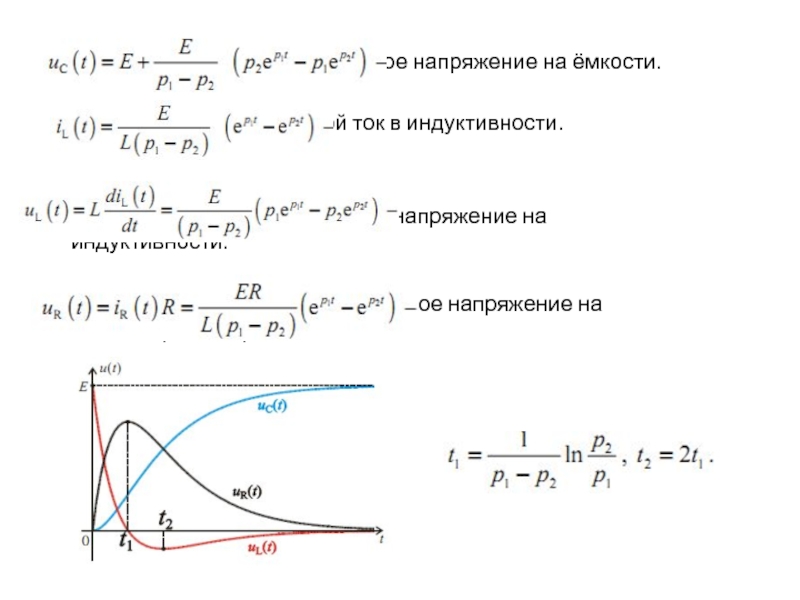
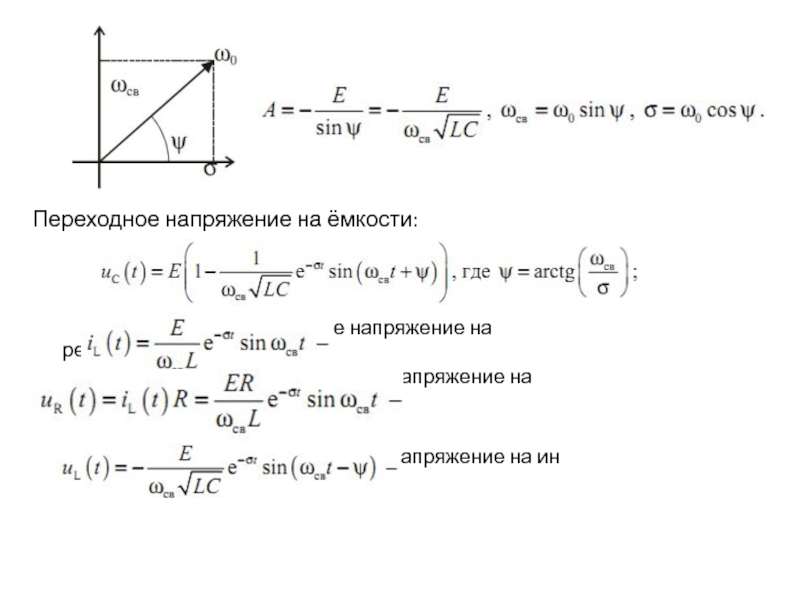
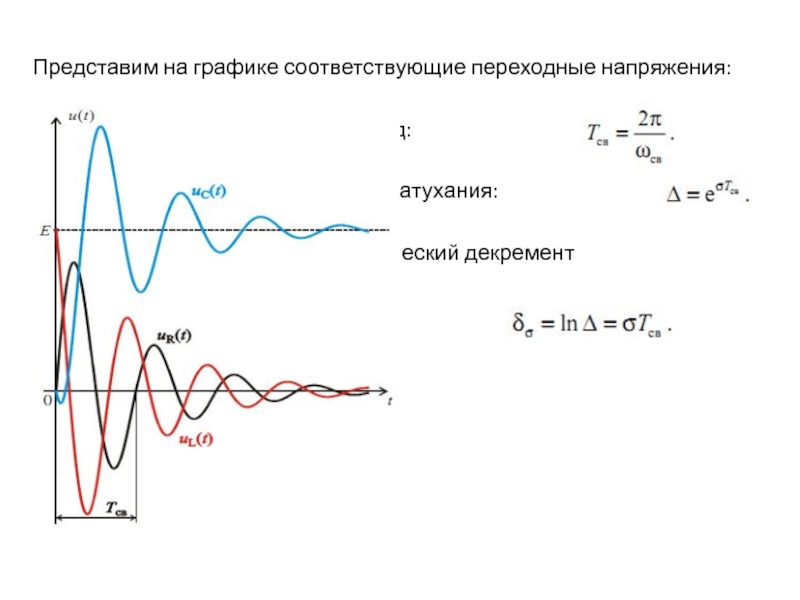
Задача: определить переходное напряжение на ёмкости и ток в индуктивности.
Напряжение на ёмкости до коммутации:
Ток в индуктивности до коммутации:
Согласно законам коммутации:

– задача с нулевыми начальными условиями.

Составим дифференциальное уравнение для напряжения на ёмкости (после коммутации):

характеристического уравнения.
Введём понятие критического сопротивления, определяемого из условия:

составляющая определяется
Принуждённая составляющая определяется при
Общий вид реакции:
Для определения A1

переходной ток в индуктивности.

то имеет место критический процесс.

переходной ток в индуктивности.

переходное

нулевых начальных условий получим систему уравнений:


Поскольку


После преобразований получим уравнение:
Откуда

Последнее

резисторе;
переходное напряжение на
резисторе;

переходное напряжение на ин индуктивности.

это надо учитывать. Физическое пояснение колебательного процесса.






Колебания возникают, когда есть

в обратном направлении: емкость разряжается.
Характер процесса также определяется корнями

функция.



Введём комплексную переменную:
Преобразованием

изображение.
Для сокращений записи преобразований
используем:
Обратное преобразование Лапласа:

Лапласа, получим:


Закон Ома в операторной форме при нулевых
начальных условиях:


где

ненулевых начальных условиях, то есть





Применяя преобразование Лапласа, получим:


Изображение для