Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок математики в 6 классе по теме «Золотая пропорция»
Содержание
- 1. Урок математики в 6 классе по теме «Золотая пропорция»
- 2. “…Геометрия владеет двумя сокровищами – теоремой Пифагора
- 3. Предметные области: математика, мировая художественная культура, изобразительное искусство, история
- 4. - Расширить сферу математических знаний учащихся:
- 5. «Золотое сечение»Золотое сечение, золотая пропорция, деление отрезка в среднем и крайнем отношениях.«Божественное», «чудесное», «превосходнейшее».
- 6. Деление тела точкой пупа – важнейший показатель
- 7. «Золотое сечение»Для удобства длину отрезка АВ обозначим
- 8. «Золотое сечение» в архитектуреПарфенон (V век до н.э.).
- 9. «Золотой треугольник»«Золотым» называется такой равнобедренный треугольник , основание и боковая стороны которого находятся в золотом отношении.
- 10. «Джоконда», около 1503г, Лувр Композиция основана на золотых треугольниках, которые являются частями правильного звездчатого пятиугольника.
- 11. «Золотой прямоугольник»Прямоугольник, стороны которого находятся в золотом
- 12. ПентаграммаВ переводе с греческого - «пять линий».Пентаграмма
- 13. Слайд 13
- 14. Пентаграмма представляет собой вместилище золотых пропорций! Внутри
- 15. Работа по группам«Золотое сечение»В математикеВ живописиВ музыкеВ литературеВ фотографииВ природеВ архитектуре
- 16. « Золотое сечение» в математике1) Какие существуют
- 17. « Золотое сечение» в фотографии Существуют ли
- 18. « Золотое сечение» в литературеВыяснить, что роднит
- 19. « Золотое сечение»
- 20. « Золотое сечение» в архитектуреСуществуют ли строения
- 21. « Золотое сечение» в живописиСуществуют ли картины,
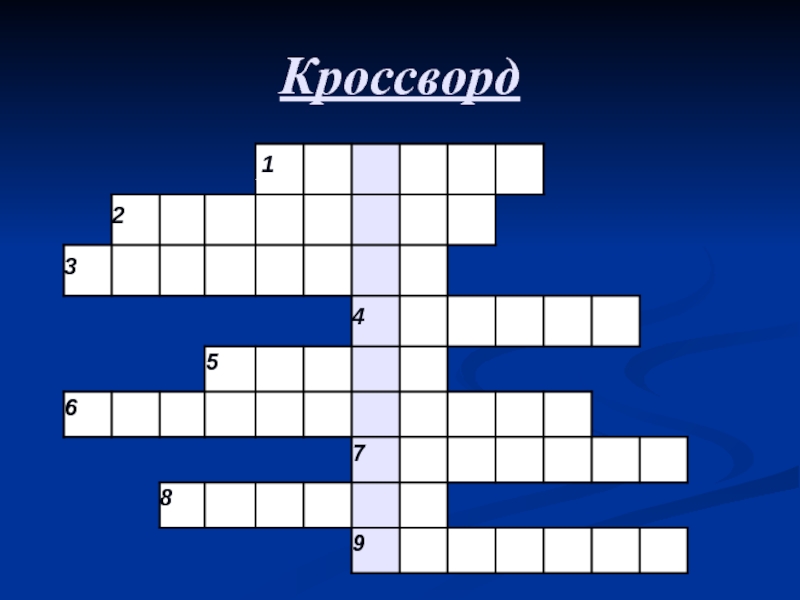
- 22. Кроссворд
- 23. По горизонтали Немецкий математик и астроном, впервые
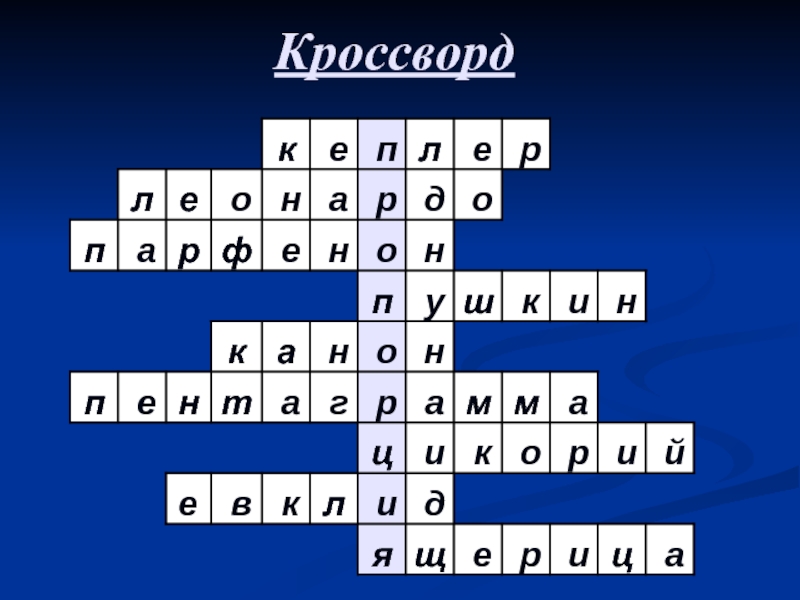
- 24. Кроссворд
- 25. Узоры математики, как и узоры художника или
- 26. Слайд 26
- 27. Желаю удачи!
- 28. Скачать презентанцию
“…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…”.
Слайды и текст этой презентации
Слайд 2“…Геометрия владеет двумя
сокровищами – теоремой Пифагора
и золотым сечением,
и если первое
из них можно сравнить с мерой золота,
то второе – с драгоценным камнем…”. Иоганн Кеплер
" Золотое сечение"
Слайд 3Предметные области:
математика, мировая художественная культура, изобразительное искусство, история
Слайд 4- Расширить сферу математических знаний учащихся:
познакомить учащихся с золотой пропорцией и связанных с нею соотношениях.
-
Развить эстетическое восприятие математических фактов: расширить представления учащихся о сферах применения математики не только в естественных науках, но и в такой области гуманитарной сферы деятельности, как искусство.- Расширить общекультурный кругозор учащихся посредством знакомства их с лучшими образцами произведений искусства.
- Продемонстрировать разнообразное применение математики в реальной жизни.
- Помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы (показать возможности применения полученных знаний в своей будущей профессии художника, архитектора, биолога, инженера-строителя).
-Научить представлять результаты своей работы с использованием информационных технологий.
Цель работы:
Слайд 5«Золотое сечение»
Золотое сечение, золотая пропорция, деление отрезка в среднем и
крайнем отношениях.
«Божественное», «чудесное», «превосходнейшее».
Слайд 6Деление тела точкой пупа – важнейший показатель «золотого сечения».
“Если
мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем
поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.Леонардо да Винчи
Слайд 7«Золотое сечение»
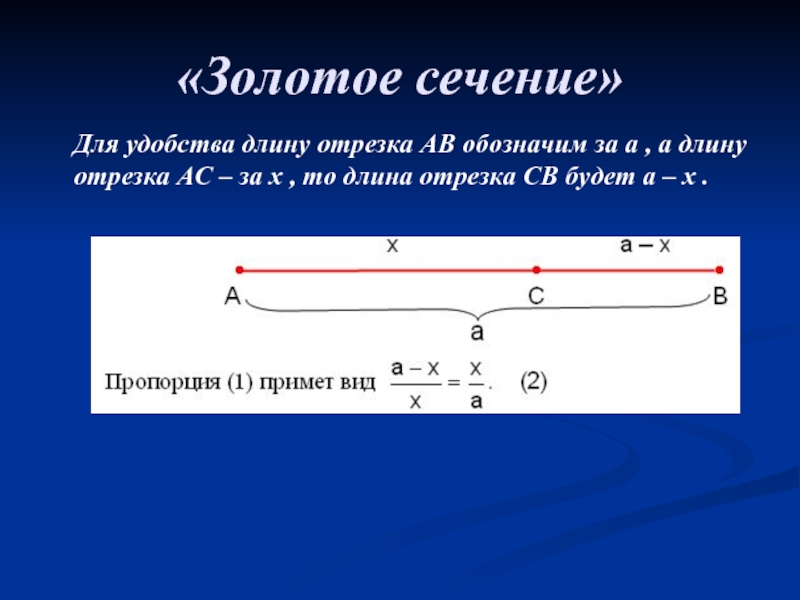
Для удобства длину отрезка АВ обозначим за а ,
а длину отрезка АС – за х , то длина
отрезка СВ будет а – х .Слайд 9«Золотой треугольник»
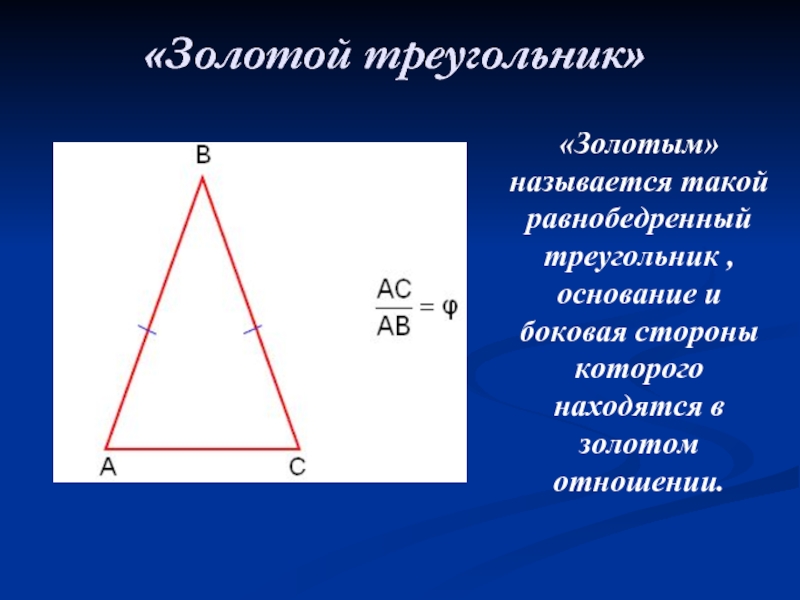
«Золотым» называется такой равнобедренный треугольник , основание и боковая
стороны которого находятся в золотом отношении.
Слайд 10«Джоконда», около 1503г, Лувр
Композиция основана на золотых треугольниках, которые
являются частями правильного звездчатого пятиугольника.
Слайд 11«Золотой прямоугольник»
Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение
ширины к длине даёт число ф , называется «золотым прямоугольником».
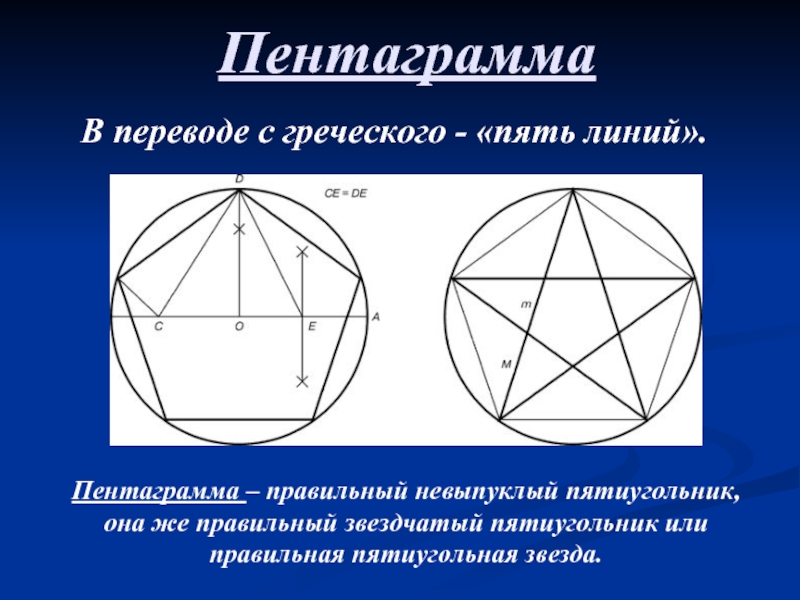
Слайд 12Пентаграмма
В переводе с греческого - «пять линий».
Пентаграмма – правильный невыпуклый
пятиугольник, она же правильный звездчатый пятиугольник или правильная пятиугольная звезда.
Слайд 14Пентаграмма представляет собой вместилище золотых пропорций!
Внутри пятиугольника можно продолжить
строить пятиугольники, и золотые отношения будут сохраняться.
Слайд 15Работа по группам
«Золотое сечение»
В математике
В живописи
В музыке
В литературе
В фотографии
В природе
В
архитектуре
Слайд 16« Золотое сечение»
в математике
1) Какие существуют подходы к определению «золотого
сечения» ?
2) Какой треугольник и прямоугольник
называются золотыми?
3)
Какие числа называют числами Фибоначчи?4) Как построить правильный пятиугольник?
Слайд 17« Золотое сечение»
в фотографии
Существуют ли рисунки, фотографии, репродукции
картин, связанные с данной темой?
Выяснить:
а) Есть ли
закономерность «золотого сечения»;б) Удовлетворяют ли приятные глазу вещи «золотому cечению».
Можно ли сфотографировать природу так, чтобы ее фотография была сделана по правилу «золотого сечения»?
Слайд 18« Золотое сечение»
в литературе
Выяснить, что роднит структуру поэтических произведений с
музыкой?
Как связаны между собой размер стихов
и числа Фибоначчи?Встречается ли «золотое сечение»
в произведениях А.С.Пушкина?
Слайд 19 « Золотое сечение»
в биологии
Встречается ли «золотое сечение»
в ботанике?
Существует ли связь между «золотым сечением» и организацией живых существ?
Какова взаимосвязь между «золотым сечением» и функциональной ассиметрией мозга?
Что общего между «золотым сечением» и деятельностью сердца?
Слайд 20« Золотое сечение»
в архитектуре
Существуют ли строения
архитекторов, выполненные по
принципу «золотого сечения»?
Если да, то можно ли провести
геометрическое исследование
по фотографиям или рисункам
этих строений?
Можно ли самим выполнить макет здания,
удовлетворяющего правилу «золотого сечения»?
Слайд 21« Золотое сечение»
в живописи
Существуют ли картины, нарисованные
по правилу
«золотого сечения»?
Если да, то можно ли провести
геометрическое исследование по фотографиям этих картин?
Возможно ли, используя
принцип «золотого сечения» ,
самим нарисовать картину?
Слайд 23По горизонтали
Немецкий математик и астроном, впервые подметивший проявления "золотого
сечения" в природе.
Назовите имя художника, который деление отрезка в отношении
Ф назвал " золотым сечением".Древнее сооружение с гармоническими пропорциями.
Многие стихи этого гениального поэта построены по законам "золотого сечения".
Как называется трактат, в котором Поликлет стремился установить законы пропорциональности человеческого тела.
Символ Пифагорейцев.
7. Растение, длина лепестков которого подчинена правилу "золотого сечения".
Автор книги "Начала", в которой впервые встречается "золотое сечение ".
У этой рептилии длина хвоста так относится к длине остального тела, как 62 к 38.
Слайд 25Узоры математики, как и узоры художника или узоры поэта, должны
быть красивы; идеи, как и краски или слова, должны сочетаться
гармонически. Красота является первым критерием: в мире нет места для безобразной математики. Дж. Х. Харди
Теги