Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Усечённая пирамида
Содержание
- 1. Усечённая пирамида
- 2. Плоскость, параллельная плоскости основания пирамиды и пересекающая
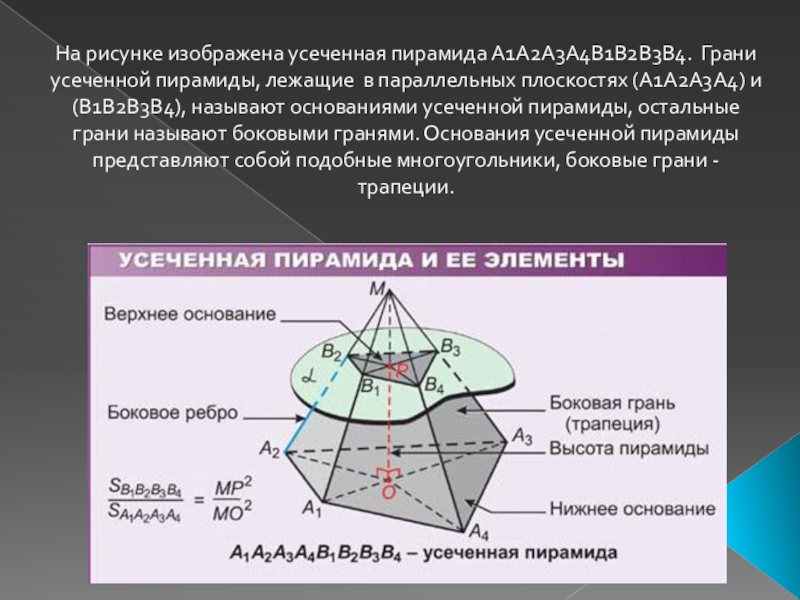
- 3. На рисунке изображена усеченная пирамида A1А2А3А4В1В2В3В4. Грани
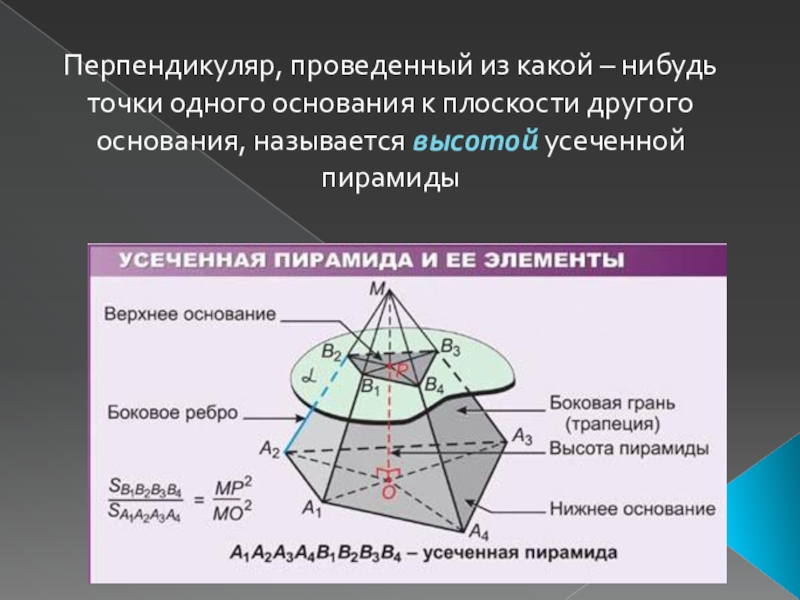
- 4. Перпендикуляр, проведенный из какой – нибудь точки
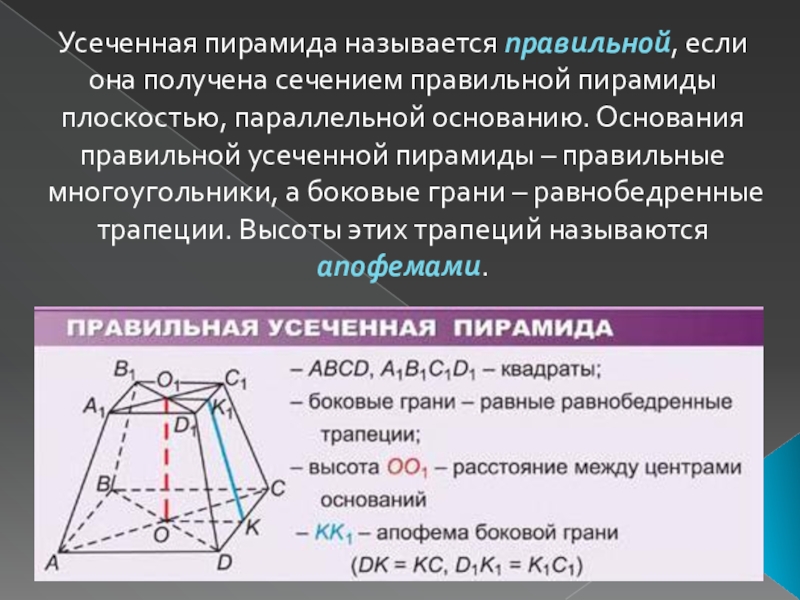
- 5. Усеченная пирамида называется правильной, если она получена
- 6. Правильная усеченная пирамида также как и обычная
- 7. Теорема: Площадь боковой поверхности правильной усечённой пирамиды
- 8. Объем усеченной пирамиды:V = 1/3H(S +√SS´ +
- 9. Скачать презентанцию
Плоскость, параллельная плоскости основания пирамиды и пересекающая пирамиду, отсекает от нее подобную пирамиду. Другая часть пирамиды представляет собой многогранник, который называют усеченной пирамидой.
Слайды и текст этой презентации
Слайд 3На рисунке изображена усеченная пирамида A1А2А3А4В1В2В3В4. Грани усеченной пирамиды, лежащие
в параллельных плоскостях (A1А2А3А4) и (B1В2В3В4), называют основаниями усеченной пирамиды,
остальные грани называют боковыми гранями. Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани - трапеции.Слайд 4Перпендикуляр, проведенный из какой – нибудь точки одного основания к
плоскости другого основания, называется высотой усеченной пирамиды
Слайд 5Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды
плоскостью, параллельной основанию. Основания правильной усеченной пирамиды – правильные многоугольники,
а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами.Слайд 6Правильная усеченная пирамида также как и обычная правильная пирамида имеет
особенности:
В правильной усеченной n-угольной пирамиде все боковые ребра равны
между собой. Все боковые грани правильной усеченной n-угольной пирамиды суть равные равнобедренные трапеции (углы при основаниях равнобедренной трапеции равны), поэтому:
В правильной усеченной n-угольной пирамиде все плоские углы при основаниях равны.
В правильной усеченной n-угольной пирамиде все двугранные углы при основаниях равны.
В правильной усеченной n-угольной пирамиде все двугранные углы при боковых ребрах равны.