Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Устойчивость. Формула Эйлера
Содержание
- 1. Устойчивость. Формула Эйлера
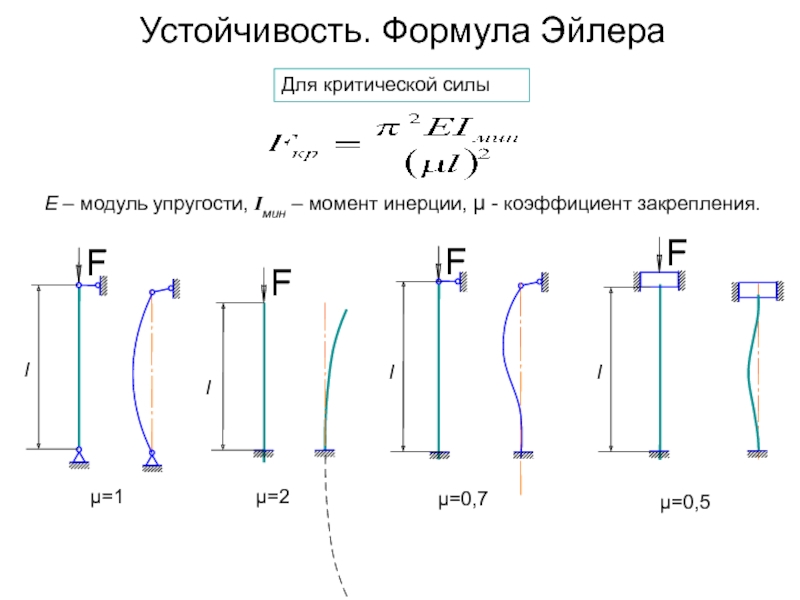
- 2. Устойчивость. Формула Эйлераμ=1μ=2μ=0,7μ=0,5lДля критической силыЕ – модуль упругости, Iмин – момент инерции, μ - коэффициент закрепления.
- 3. Устойчивость. Формула ЭйлераДля критического напряженияРадиус инерцииГибкость сжатой стойки
- 4. Формула Феликса ЯсинскогоДля критической силыДля критического напряженияЗдесь
- 5. Полный график критических напряженийσλ0Напряжения в стойке не
- 6. Сложное сопротивлениеСложный и косой изгибПод сложным сопротивлением
- 7. Сложный и косой изгибПод косым изгибом понимают
- 8. Сложный и косой изгибНапряжения при косом изгибеПри
- 9. Сложный и косой изгибНейтральная линия поперечного сечения
- 10. Внецентренное растяжение (сжатие)Внецентренным растяжением или сжатием называется
- 11. Внецентренное растяжение (сжатие)Уравнение нейтральной линии при внецентренном
- 12. Геометрические характеристики плоских сеченийПод статическим моментом площади
- 13. Моментом инерции площади относительно оси называется сумма
- 14. Моменты инерции практически важных сеченийПрямоугольное сечение
- 15. Моменты инерции практически важных сеченийКруглое сечениеТрубчатое сечение
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Устойчивость. Формула Эйлера
μ=1
μ=2
μ=0,7
μ=0,5
l
Для критической силы
Е – модуль упругости, Iмин –
момент инерции, μ - коэффициент закрепления.
Слайд 4Формула Феликса Ясинского
Для критической силы
Для критического напряжения
Здесь a и b
– постоянный коэффициенты зависящие от материала стойки
Значения коэффициентов a и
b, МПаСлайд 5Полный график критических напряжений
σ
λ
0
Напряжения в стойке не должны превышать предела
пропорциональности
Гибкость стойки в этом случае должна удовлетворять условию
Для стали Ст.
3 λпр =100Ст.5 λпр=85
Для чугуна λпр=80
Для древесины λпр=70
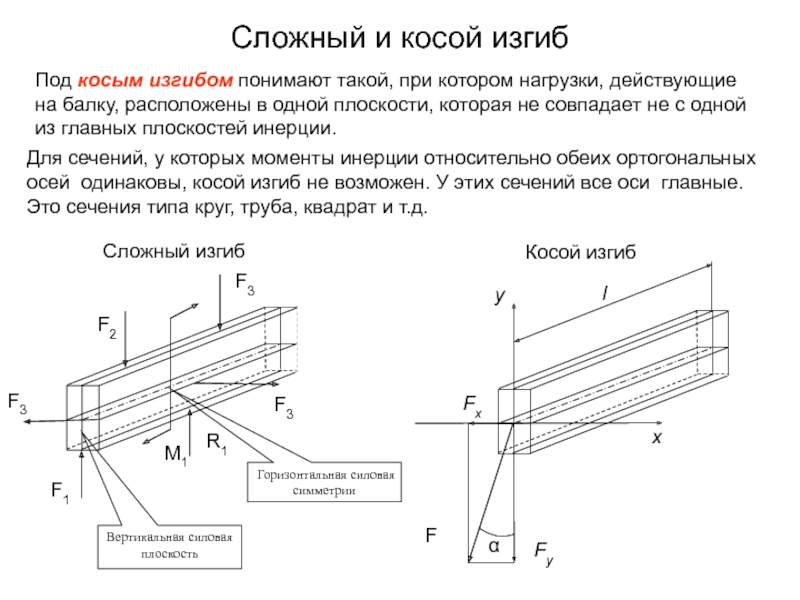
Слайд 6Сложное сопротивление
Сложный и косой изгиб
Под сложным сопротивлением подразумевают деформации бруса
возникающие в результате комбинации, в различных сочетаниях, простых видов деформаций:
растяжения (сжатия), среза, кручения и изгиба.Сложным называется изгиб, вызванный силами или моментами, расположенными в двух и более плоскостях, проходящих через ось балки. Эти плоскости могут, как совпадать, так и не совпадать с главными плоскостями инерции
В том и другом случаях, наиболее удобным решением является приведение к двум плоским изгибам.
Для этого необходимо:
спроектировать все действующие силы на две главные плоскости;
рассмотреть изгиб в каждой из двух главных плоскостей отдельно;
пользуясь принципом независимости действия сил найти суммарные напряжения или деформации.
В большинстве случаев в опасной точке поперечного сечения бруса касательные напряжения, либо равны нулю, либо весьма малы по сравнению с нормальными напряжениями, поэтому расчеты на прочность при сложном и косом изгибе ведут с учетом только нормальных напряжений.
Слайд 7Сложный и косой изгиб
Под косым изгибом понимают такой, при котором
нагрузки, действующие на балку, расположены в одной плоскости, которая не
совпадает не с одной из главных плоскостей инерции.Для сечений, у которых моменты инерции относительно обеих ортогональных осей одинаковы, косой изгиб не возможен. У этих сечений все оси главные. Это сечения типа круг, труба, квадрат и т.д.
Слайд 8Сложный и косой изгиб
Напряжения при косом изгибе
При определении знака нормального
напряжения необходимо придерживаться правила, по которому момент, вызывающий деформацию растяжения
в первой четверти поперечного сечения считается положительным, тогда знак напряжения определяется знаком координат точки, в которой определяется напряжение.здесь: MX, MY – составляющие изгибающего момента; M- полный изгибающий момент в сечении; α - угол между осью y и следом плоскости действия полного момента; x и у координаты точки, в которой определяют напряжения; Ix и Iy - моменты инерции поперечного сечения.
Напряжения при сложном изгибе
Условие прочности при косом изгибе
Условие прочности при сложном изгибе
Слайд 9Сложный и косой изгиб
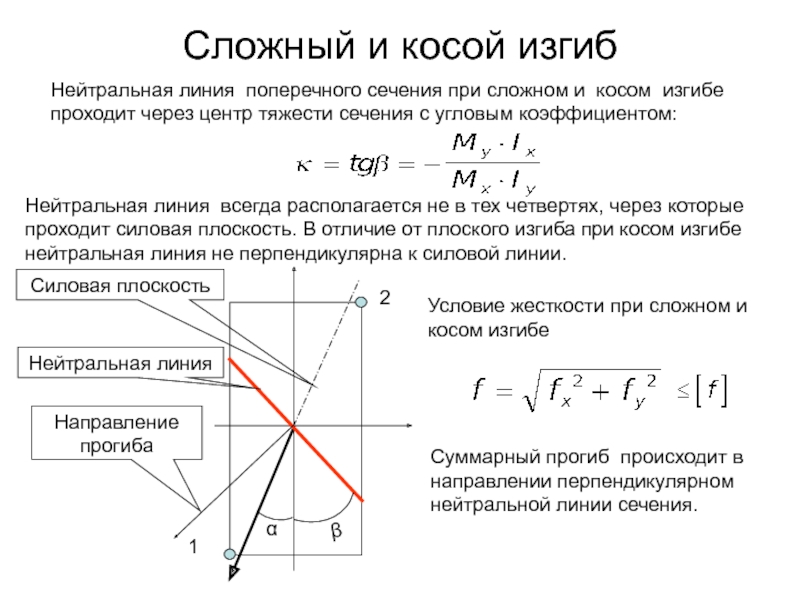
Нейтральная линия поперечного сечения при сложном и
косом изгибе проходит через центр тяжести сечения с угловым коэффициентом:
Нейтральная
линия всегда располагается не в тех четвертях, через которые проходит силовая плоскость. В отличие от плоского изгиба при косом изгибе нейтральная линия не перпендикулярна к силовой линии.Силовая плоскость
Нейтральная линия
Условие жесткости при сложном и косом изгибе
Суммарный прогиб происходит в направлении перпендикулярном нейтральной линии сечения.
Направление прогиба
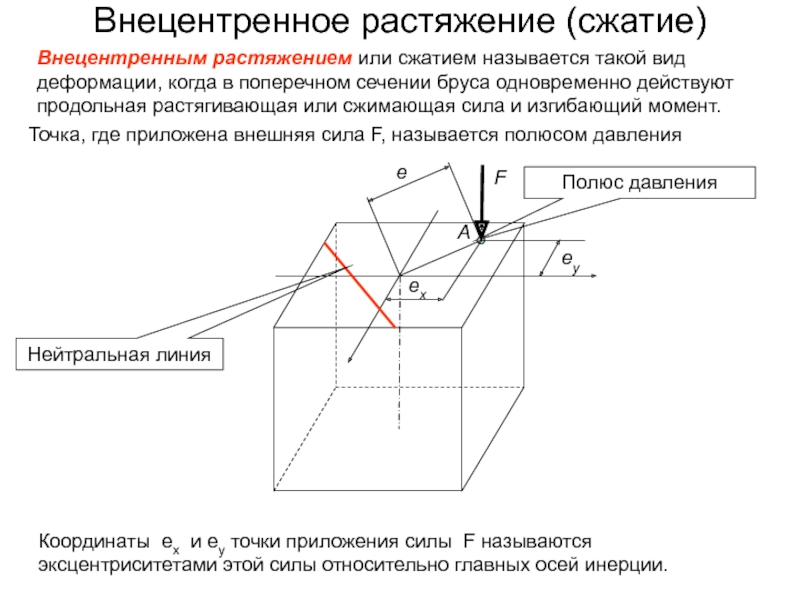
Слайд 10Внецентренное растяжение (сжатие)
Внецентренным растяжением или сжатием называется такой вид деформации,
когда в поперечном сечении бруса одновременно действуют продольная растягивающая или
сжимающая сила и изгибающий момент.Координаты ex и ey точки приложения силы F называются эксцентриситетами этой силы относительно главных осей инерции.
Точка, где приложена внешняя сила F, называется полюсом давления
Полюс давления
Нейтральная линия
Слайд 11Внецентренное растяжение (сжатие)
Уравнение нейтральной линии при внецентренном растяжении (сжатии):
Нейтральная линия
не проходит через центр тяжести сечения и пересекает координатные оси
в точках, принадлежащих квадранту, противоположному тому, в котором находится точка приложения силы.здесь F- внешняя продольная сила; x и y - координаты точки в которой определяются нормальные напряжения; ex и ey - координаты точки приложения внешней силы (эксцентриситеты); Ix и Iy - моменты инерции сечения относительно главных центральных осей; А- площадь поперечного сечения.
Нормальные напряжения при внецентренном растяжении (сжатии)
Слайд 12Геометрические характеристики плоских сечений
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на расстояния от их
центра тяжести до соответствующей оси:Различают следующие характеристики сечений: площадь S, статический момент площади (WX, или WY ), момент инерции площади (IX, или IY), центробежный момент инерции площади (IXY).
Оси, проходящие через центр тяжести, называются центральными осями.
Моменты площади фигуры относительно центральных осей равны нулю
Координаты центра тяжести
Слайд 13Моментом инерции площади относительно оси называется сумма произведений площадей элементарных
площадок на квадрат расстояний от их центра тяжести до соответствующей
оси.Центробежным моментом инерции называется сумма произведений площадей элементарных площадок на расстояния от центра тяжести до осей
Полярным моментом инерции называется сумма произведения площадей элементарных площадок на квадрат расстояния от центра тяжести до начала координат
Полярный момент инерции равен сумме осевых моментов инерции относительно взаимно перпендикулярных осей.
Геометрические характеристики плоских сечений