Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Устойчивость гидродинамических течений
Содержание
- 1. Устойчивость гидродинамических течений
- 2. Глобальный отрыв над пластинкой под углом атакиПо
- 3. Обтекание кругового цилиндра По мере увеличения скорости
- 4. Обтекание шараПри этой скорости, лишь слегка превышающей
- 5. Неустойчивость обтекания шараМгновенная картина обтекания шара Подкраска
- 6. Осредненный поток при обтекании шара с турбулизирующей
- 7. След за телом вращения с плоским дномЛаминарный
- 8. Развитие вихрей на ускоренно движущейся пластинкеСделанные искровым
- 9. Вихревая дорожка Кармана за круговым цилиндром при
- 10. Неустойчивость осесимметричной струи.Ламинарный поток воздуха вытекает из
- 11. Неустойчивость пограничного слоя на пластинкеПри рассчитанном по
- 12. Неустойчивость дымовой струйки от сигареты.На этих двух
- 13. В природе все гидродинамические течения и процессы
- 14. Общее решение линеаризованной системы уравнений Навье-Стокса можно
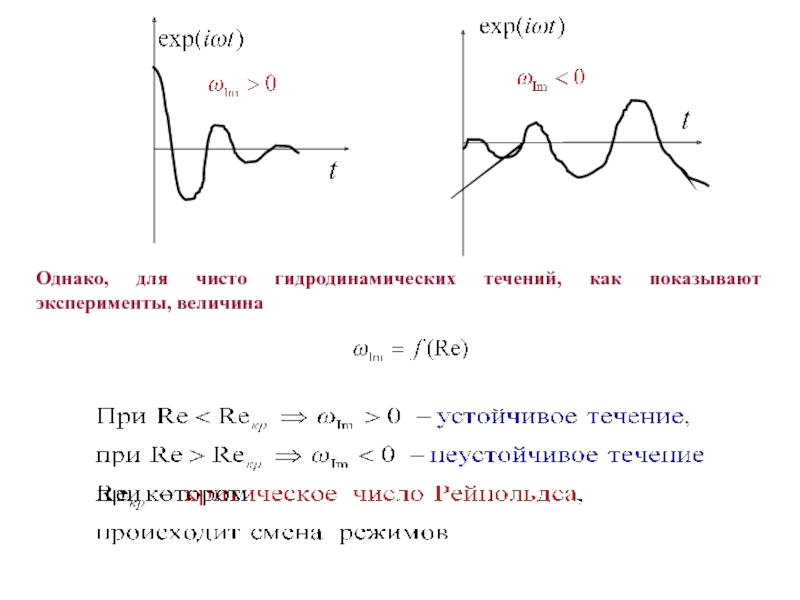
- 15. Однако, для чисто гидродинамических течений, как показывают эксперименты, величина
- 16. 5. 3. Устойчивость течения в трубе (устойчивость
- 17. Исходное течениеВозмущенное течение Исходное течениеУстойчивость!Неустойчивость!Новое течениеДля плоского
- 18. Для течения Пуазейля в круглой трубе:Для течения
- 19. 5. 4. Неустойчивость ламинарного пограничного слояxуПотенциальное течениеПри
- 20. Схема основных стадий процесса перехода к турбулентности
- 21. Схема активного контроля процесса перехода к турбулентности
- 22. При определенных условиях – возможна не только
- 23. Ламинарный отрыв на искривленной стенкеВоздушные пузырьки в
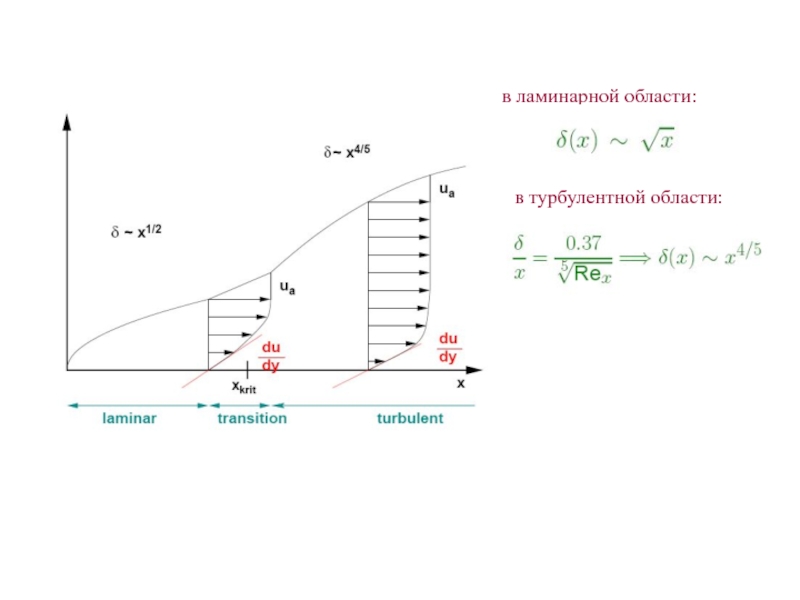
- 24. в турбулентной области:в ламинарной области:
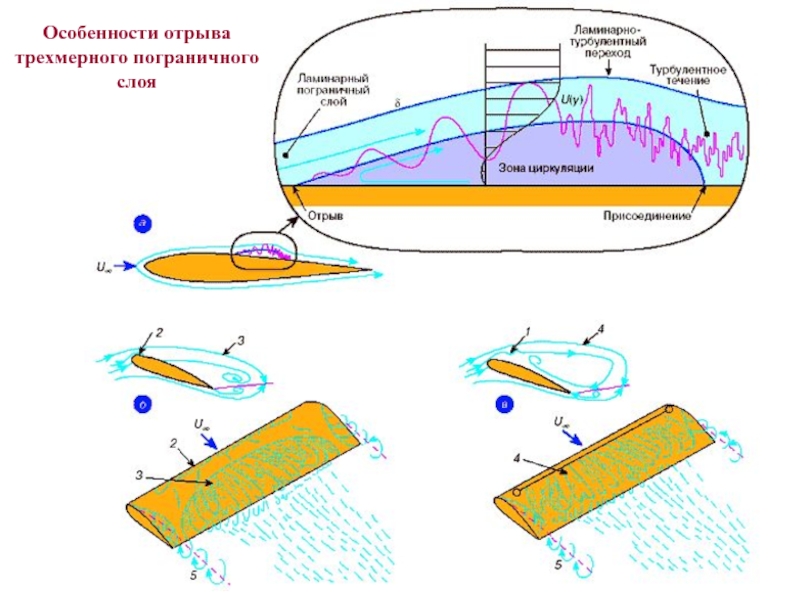
- 25. Особенности отрыва трехмерного пограничного слоя
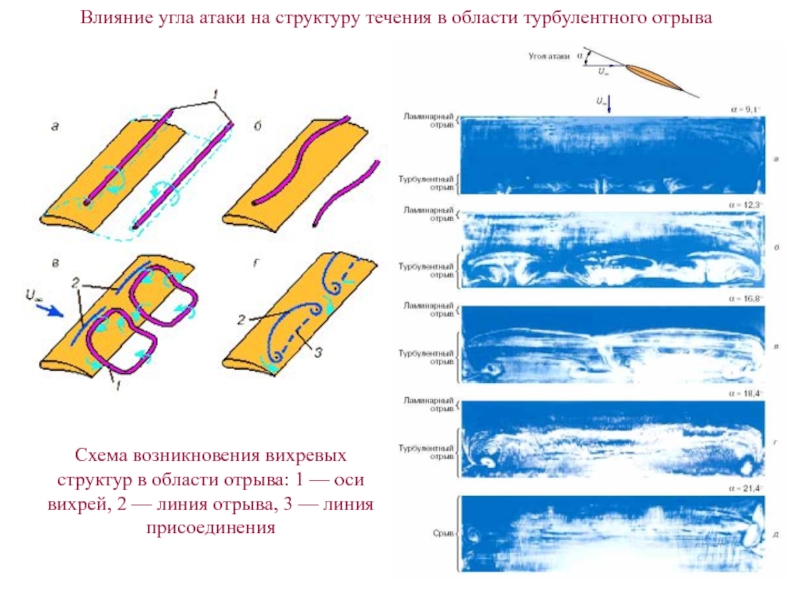
- 26. Влияние угла атаки на структуру течения в
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 15. Устойчивость гидродинамических течений
Образование вихревой структуры
при обтекании крыла
5.1. Примеры
неустойчивых гидродинамических течений
струи жидкости в другой жидкости при увеличивающемся числе РейнольдсаСлайд 2Глобальный отрыв над пластинкой под углом атаки
По мере увеличения угла
атаки локальная зона ламинарного отрыва у передней кромки, показанная выше,
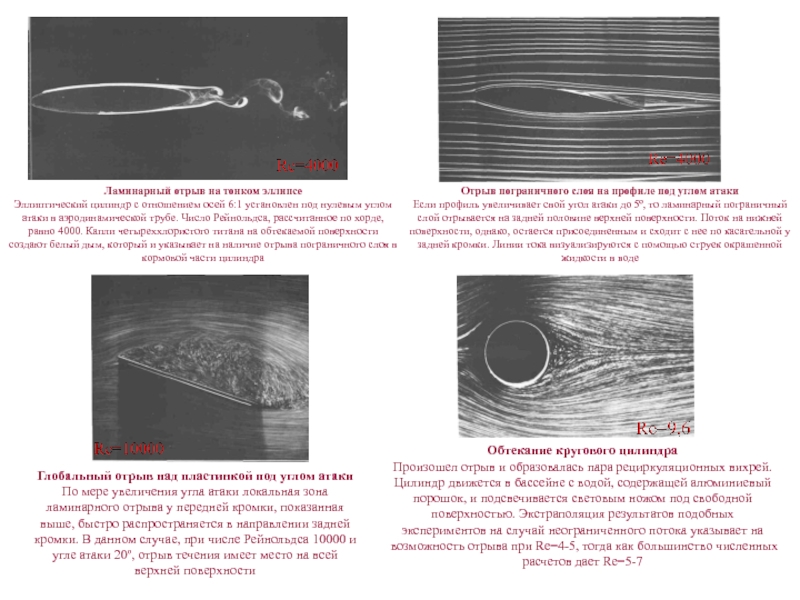
быстро распространяется в направлении задней кромки. В данном случае, при числе Рейнольдса 10000 и угле атаки 20º, отрыв течения имеет место на всей верхней поверхностиОбтекание кругового цилиндра
Произошел отрыв и образовалась пара рециркуляционных вихрей. Цилиндр движется в бассейне с водой, содержащей алюминиевый порошок, и подсвечивается световым ножом под свободной поверхностью. Экстраполяция результатов подобных экспериментов на случай неограниченного потока указывает на возможность отрыва при Re=4-5, тогда как большинство численных расчетов дает Re=5-7
Ламинарный отрыв на тонком эллипсе
Эллиптический цилиндр с отношением осей 6:1 установлен под нулевым углом атаки в аэродинамической трубе. Число Рейнольдса, рассчитанное по хорде, равно 4000. Капли четыреххлористого титана на обтекаемой поверхности создают белый дым, который и указывает на наличие отрыва пограничного слоя в кормовой части цилиндра
Отрыв пограничного слоя на профиле под углом атаки
Если профиль увеличивает свой угол атаки до 5º, то ламинарный пограничный слой отрывается на задней половине верхней поверхности. Поток на нижней поверхности, однако, остается присоединенным и сходит с нее по касательной у задней кромки. Линии тока визуализируются с помощью струек окрашенной жидкости в воде
Слайд 3Обтекание кругового цилиндра
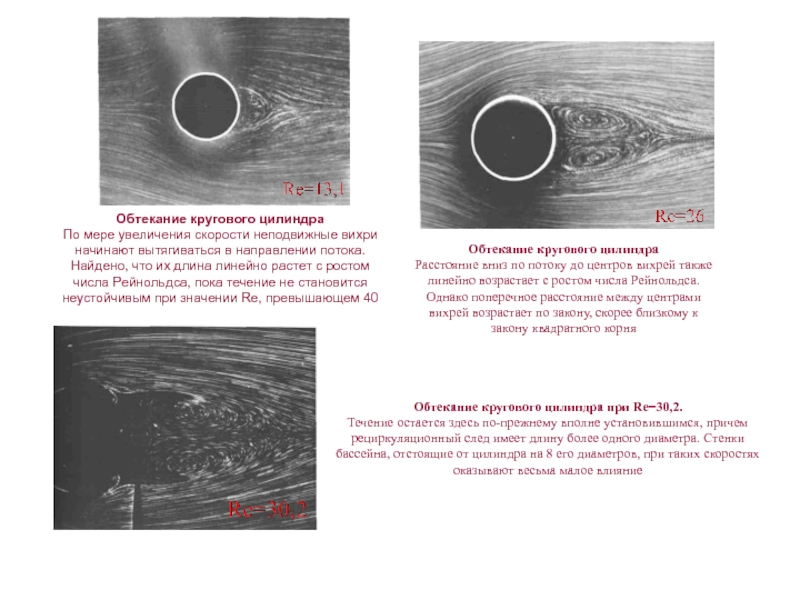
По мере увеличения скорости неподвижные вихри начинают
вытягиваться в направлении потока. Найдено, что их длина линейно растет
с ростом числа Рейнольдса, пока течение не становится неустойчивым при значении Re, превышающем 40Обтекание кругового цилиндра
Расстояние вниз по потоку до центров вихрей также линейно возрастает с ростом числа Рейнольдса. Однако поперечное расстояние между центрами вихрей возрастает по закону, скорее близкому к закону квадратного корня
Обтекание кругового цилиндра при Re=30,2.
Течение остается здесь по-прежнему вполне установившимся, причем рециркуляционный след имеет длину более одного диаметра. Стенки бассейна, отстоящие от цилиндра на 8 его диаметров, при таких скоростях оказывают весьма малое влияние
Слайд 4Обтекание шара
При этой скорости, лишь слегка превышающей скорость течения на
предыдущем снимке, поток уже явно становится отрывным в кормовой области
шара; при этом образуется тонкое неподвижное вихревое кольцо.Неустойчивость обтекания шара
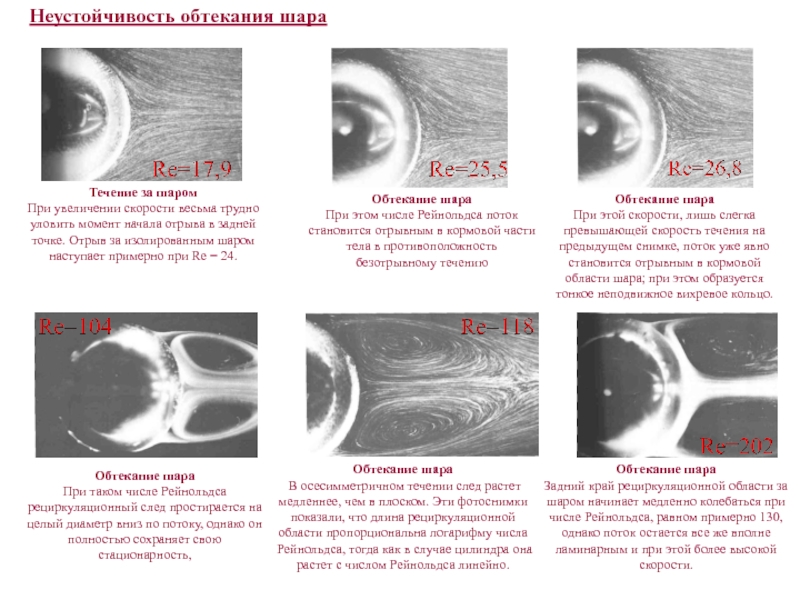
Обтекание шара
При этом числе Рейнольдса поток становится отрывным в кормовой части тела в противоположность безотрывному течению
Течение за шаром
При увеличении скорости весьма трудно уловить момент начала отрыва в задней точке. Отрыв за изолированным шаром наступает примерно при Re = 24.
Обтекание шара
При таком числе Рейнольдса рециркуляционный след простирается на целый диаметр вниз по потоку, однако он полностью сохраняет свою стационарность,
Обтекание шара
В осесимметричном течении след растет медленнее, чем в плоском. Эти фотоснимки показали, что длина рециркуляционной области пропорциональна логарифму числа Рейнольдса, тогда как в случае цилиндра она растет с числом Рейнольдса линейно.
Обтекание шара
Задний край рециркуляционной области за шаром начинает медленно колебаться при числе Рейнольдса, равном примерно 130, однако поток остается все же вполне ламинарным и при этой более высокой скорости.
Слайд 5Неустойчивость обтекания шара
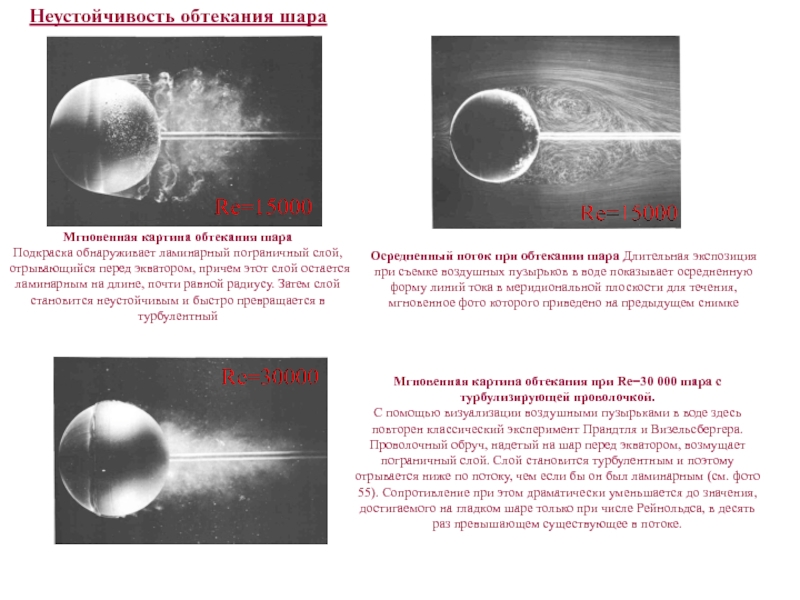
Мгновенная картина обтекания шара
Подкраска обнаруживает ламинарный пограничный
слой, отрывающийся перед экватором, причем этот слой остается ламинарным на
длине, почти равной радиусу. Затем слой становится неустойчивым и быстро превращается в турбулентныйОсредненный поток при обтекании шара Длительная экспозиция при съемке воздушных пузырьков в воде показывает осредненную форму линий тока в меридиональной плоскости для течения, мгновенное фото которого приведено на предыдущем снимке
Мгновенная картина обтекания при Re=30 000 шара с турбулизирующей проволочкой.
С помощью визуализации воздушными пузырьками в воде здесь повторен классический эксперимент Прандтля и Визельсбергера. Проволочный обруч, надетый на шар перед экватором, возмущает пограничный слой. Слой становится турбулентным и поэтому отрывается ниже по потоку, чем если бы он был ламинарным (см. фото 55). Сопротивление при этом драматически уменьшается до значения, достигаемого на гладком шаре только при числе Рейнольдса, в десять раз превышающем существующее в потоке.
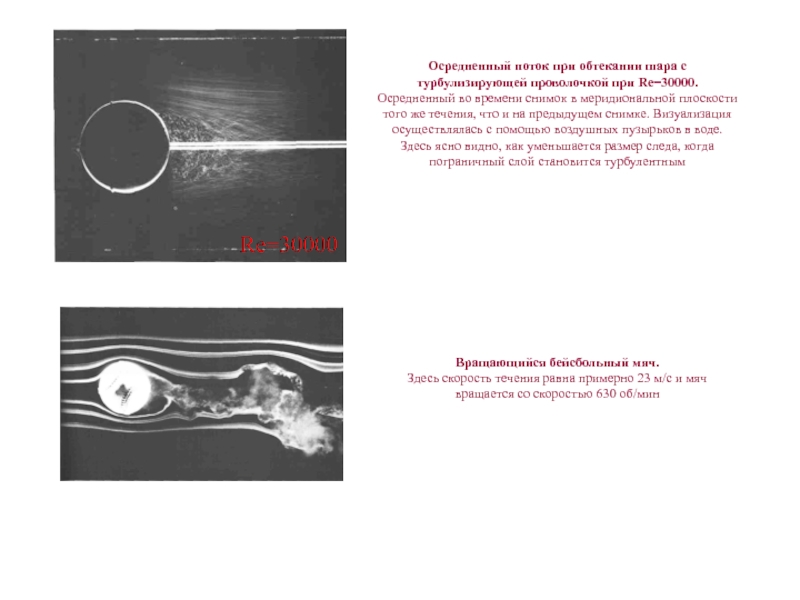
Слайд 6Осредненный поток при обтекании шара с турбулизирующей проволочкой при Re=30000.
Осредненный
во времени снимок в меридиональной плоскости того же течения, что
и на предыдущем снимке. Визуализация осуществлялась с помощью воздушных пузырьков в воде. Здесь ясно видно, как уменьшается размер следа, когда пограничный слой становится турбулентнымВращающийся бейсбольный мяч.
Здесь скорость течения равна примерно 23 м/с и мяч вращается со скоростью 630 об/мин
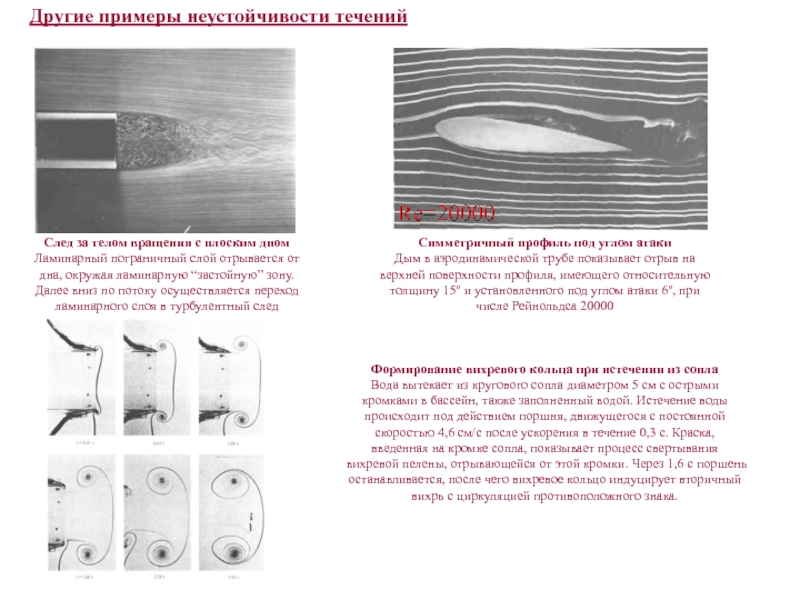
Слайд 7След за телом вращения с плоским дном
Ламинарный пограничный слой отрывается
от дна, окружая ламинарную “застойную” зону. Далее вниз по потоку
осуществляется переход ламинарного слоя в турбулентный следДругие примеры неустойчивости течений
Симметричный профиль под углом атаки
Дым в аэродинамической трубе показывает отрыв на верхней поверхности профиля, имеющего относительную толщину 15º и установленного под углом атаки 6º, при числе Рейнольдса 20000
Формирование вихревого кольца при истечении из сопла
Вода вытекает из кругового сопла диаметром 5 см c острыми кромками в бассейн, также заполненный водой. Истечение воды происходит под действием поршня, движущегося с постоянной скоростью 4,6 см/с после ускорения в течение 0,3 c. Краска, введенная на кромке сопла, показывает процесс свертывания вихревой пелены, отрывающейся от этой кромки. Через 1,6 с поршень останавливается, после чего вихревое кольцо индуцирует вторичный вихрь с циркуляцией противоположного знака.
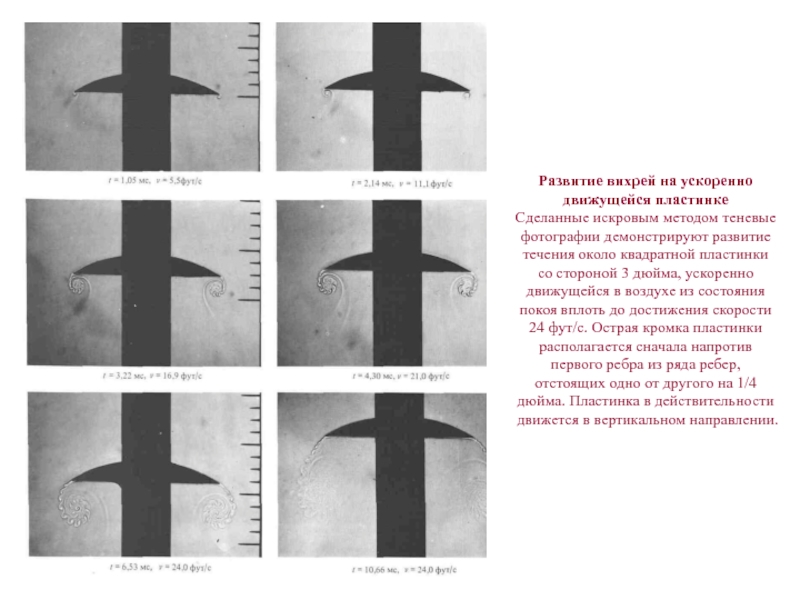
Слайд 8Развитие вихрей на ускоренно движущейся пластинке
Сделанные искровым методом теневые фотографии
демонстрируют развитие течения около квадратной пластинки со стороной 3 дюйма,
ускоренно движущейся в воздухе из состояния покоя вплоть до достижения скорости 24 фут/с. Острая кромка пластинки располагается сначала напротив первого ребра из ряда ребер, отстоящих одно от другого на 1/4 дюйма. Пластинка в действительности движется в вертикальном направлении.Слайд 9Вихревая дорожка Кармана за круговым цилиндром при Re = 140.
Вода
обтекает цилиндр диаметром 1 см co скоростью 1,4 см/с. Визуализация
движения осуществляется так: частицы метятся белым коллоидным дымом, создаваемым электролитическим способом и освещаются световым ножом. Видно, что по мере продвижения вниз по потоку на несколько диаметров ширина вихревой пелены возрастаетВихревая дорожка Кармана за круговым цилиндром при Re=200.
Этот снимок, сделанный на другой жидкости, оказался соответствующим такому моменту времени, что картина течения обладает замечательным сходством с картиной, представленной на предыдущем снимке. Течение происходит в аэродинамической трубе малой турбулентности; вверх по потоку от цилиндра вводится тонкая пелена табачного дыма
Подковообразные вихри в ламинарном пограничном слое, вид сбоку.
Сбоку видно, как вихревые петли, по меpe своего продвижения вниз no потоку поднимаются значительно выше границы пограничного слоя
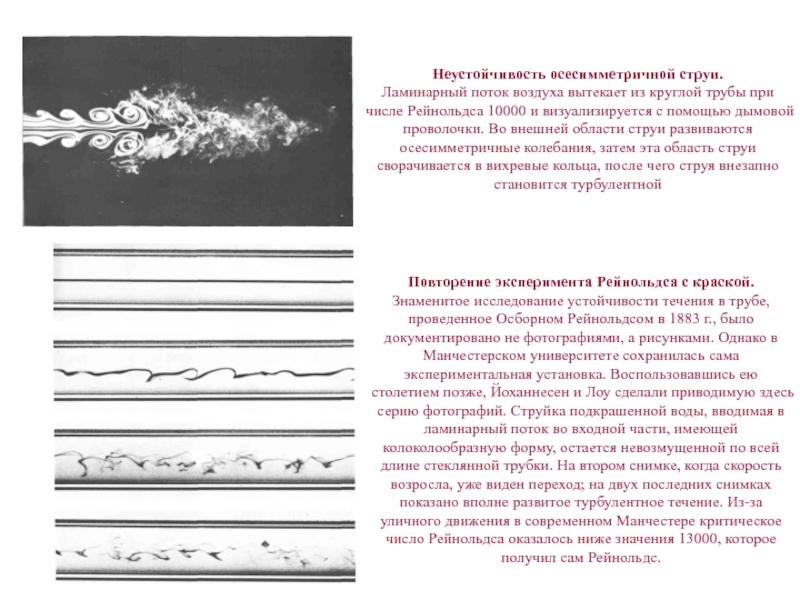
Слайд 10Неустойчивость осесимметричной струи.
Ламинарный поток воздуха вытекает из круглой трубы при
числе Рейнольдса 10000 и визуализируется с помощью дымовой проволочки. Во
внешней области струи развиваются осесимметричные колебания, затем эта область струи сворачивается в вихревые кольца, после чего струя внезапно становится турбулентнойПовторение эксперимента Рейнольдса с краской.
Знаменитое исследование устойчивости течения в трубе, проведенное Осборном Рейнольдсом в 1883 г., было документировано не фотографиями, а рисунками. Однако в Манчестерском университете сохранилась сама экспериментальная установка. Воспользовавшись ею столетием позже, Йоханнесен и Лоу сделали приводимую здесь серию фотографий. Струйка подкрашенной воды, вводимая в ламинарный поток во входной части, имеющей колоколообразную форму, остается невозмущенной по всей длине стеклянной трубки. На втором снимке, когда скорость возросла, уже виден переход; на двух последних снимках показано вполне развитое турбулентное течение. Из-за уличного движения в современном Манчестере критическое число Рейнольдса оказалось ниже значения 13000, которое получил сам Рейнольдс.
Слайд 11Неустойчивость пограничного слоя на пластинке
При рассчитанном по длине числе Рейнольдса
Re=20000 (верхний снимок) пограничный слой на пластинке, помещенной вдоль потока,
ламинарен. При Re=100000 (нижний снимок) появляются двумерные волны Толлмина-Шлихтинга. Они становятся видимыми благодаря подкрашенной жидкостиЕстественный переход на слабонаклоненной пластинке.
При том же числе Рейнольдса 100000, но при угле атаки в 1º на пластинке происходит переход к турбулентности
Переход, возникающий вниз по потоку от волн Толлмина-Шлихтинга.
В левой части снимка волны двумерные; они становятся трехмерными, сворачиваясь в середине, и турбулентными - в правой части снимка. Линии меченых частиц на этом снимке, изображающем развитие процесса, были получены подкрашиванием воды
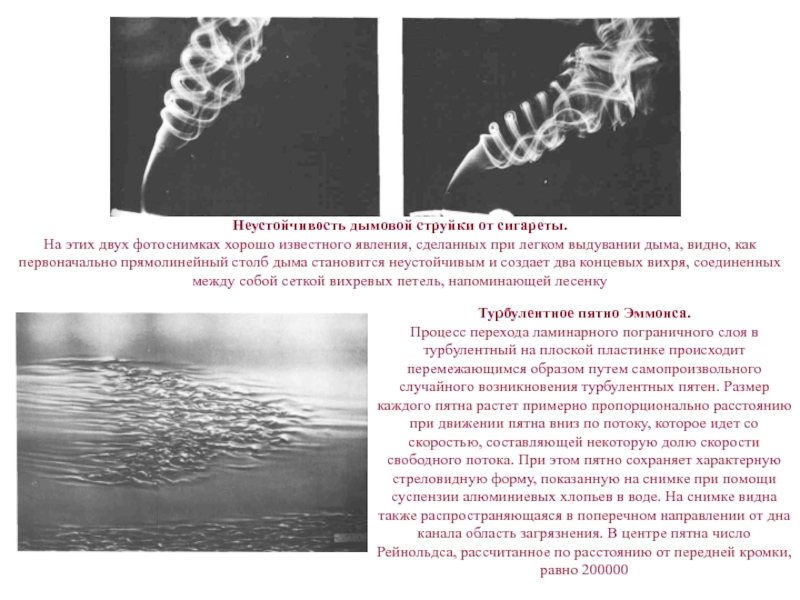
Слайд 12Неустойчивость дымовой струйки от сигареты.
На этих двух фотоснимках хорошо известного
явления, сделанных при легком выдувании дыма, видно, как первоначально прямолинейный
столб дыма становится неустойчивым и создает два концевых вихря, соединенных между собой сеткой вихревых петель, напоминающей лесенкуТурбулентное пятно Эммонса.
Процесс перехода ламинарного пограничного слоя в турбулентный на плоской пластинке происходит перемежающимся образом путем самопроизвольного случайного возникновения турбулентных пятен. Размер каждого пятна растет примерно пропорционально расстоянию при движении пятна вниз по потоку, которое идет со скоростью, составляющей некоторую долю скорости свободного потока. При этом пятно сохраняет характерную стреловидную форму, показанную на снимке при помощи суспензии алюминиевых хлопьев в воде. На снимке видна также распространяющаяся в поперечном направлении от дна канала область загрязнения. В центре пятна число Рейнольдса, рассчитанное по расстоянию от передней кромки, равно 200000
Слайд 13В природе все гидродинамические течения и процессы должны удовлетворять уравнениям
и граничным условия, но и быть устойчивыми: малые возмущения течений
должны затухать со временем.В противном случае, всегда имеющиеся в любых гидродинамических течениях малые возмущения могут возрастать со временем, что приводит к неустойчивости исходного течения и возникновению новых режимов течений. Ламинарные течения, таким образом, наблюдаются только при ограниченных числах Рейнольдса. При возрастании чисел Рейнольдса течение может начать усиливать случайные возмущения, передавая им свою энергию. Таким образом, течение становится неустойчивым.
Метод исследования устойчивости течений сводится к следующим процедурам:
Пусть существует стационарное течение, которое описывается распределением скорости
Наложим на это стационарное течение нестационарное возмущение вида
В этом случае результирующее движение есть , и, подставляя в уравнения Навье-Стокса, а также учитывая, что для стационарного исходного течения (рассматривается, для простоты, несжимаемая жидкость), получим для возмущений
5.2. Общая постановка задач устойчивости гидродинамических течений
Слайд 14Общее решение линеаризованной системы уравнений Навье-Стокса можно искать в виде
простой зависимости от времени (аналогично для давления):
В свою очередь,
зависящие от координат функции можно записать в форме: Последнее решение можно искать в рамках стационарной задачи с учетом соответствующих граничных условий. Отсюда будут найдены соответствующие функции . Более важным является поведение функций, зависящих от времени. Поскольку в общем случае
Если
- решение устойчиво (возмущения затухает со временем)
- решение неустойчиво (возмущения возрастает со временем)
Таким образом, можно получить ответ, устойчиво ли данное гидродинамическое течение или нет!
Слайд 165. 3. Устойчивость течения в трубе (устойчивость течения Пуазейля)
Рассмотрим устойчивость
течения Пуазейля (течение в трубе). Вопрос: являются ли течения в
трубах различного сечения устойчивыми при любых числах Рейнольдса?Ввиду однородности профиля скорости вдоль оси x, скорость исходного течения от этой координаты не зависит.
Поэтому решение, согласно изложенному выше подходу к изучению неустойчивости, можно искать в виде (выбираем только одну моду возмущений, поскольку их вклад в суммарное возмущение аддитивен):
В силу сказанного ранее, должно существовать такое значение , когда величина впервые обращается (при некотором значении k) в нуль.
Область неустойчивости можно определить, решив соответствующие уравнения с заданными граничными условиями. Таким образом, задача сводится к нахождению корней дисперсионного уравнения:
Решение уравнения (5.2) будет определять так называемую нейтральную кривую, которая делит области устойчивых и неустойчивых течений.
(5.2)
(5.1)
Слайд 17
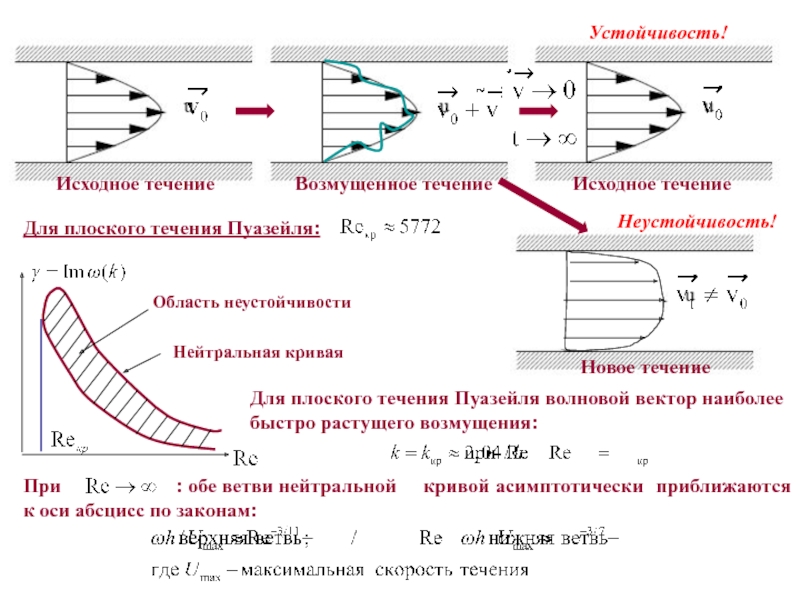
Исходное течение
Возмущенное течение
Исходное течение
Устойчивость!
Неустойчивость!
Новое течение
Для плоского течения Пуазейля:
Область
неустойчивости
Нейтральная кривая
Для плоского течения Пуазейля волновой вектор наиболее быстро растущего
возмущения: При : обе ветви нейтральной кривой асимптотически приближаются к оси абсцисс по законам:
Слайд 18Для течения Пуазейля в круглой трубе:
Для течения Пуазейля в круглой
трубе на сегодняшний день нет окончательного ответа на вопрос –
при всех ли числах Рейнольдса устойчиво это течение?Сегодня в теоретическом плане принято считать, что такое течение устойчиво относительно бесконечно малых возмущений при всех числах Рейнольдса.
Эксперимент говорит о том, что, если специальным образом стабилизировать начальные возмущения в трубе и убрать «внешний шум», то можно затянуть ламинарный режим в трубе до значений чисел Рейнольдса
Иначе обстоит дело по отношению к устойчивости относительно конечных (не малых) возмущений:
существует критическое число Рейнольдса , определяющее устойчивость течения Пуазейля относительно конечных возмущений;
при - все возмущения затухают и течение всегда устойчиво (если около входа в трубу имелись любые возмущения, то последние обязательно затухнут!);
при - конечные возмущения будут нарастать, расширяясь вдоль потока, причем чем больше , тем меньшие по амплитуде возмущения переводят течение в нестабильный режим и в режим турбулентности (см. ниже)
- для течения Пуазейля в круглой трубе!
Слайд 195. 4. Неустойчивость ламинарного пограничного слоя
x
у
Потенциальное течение
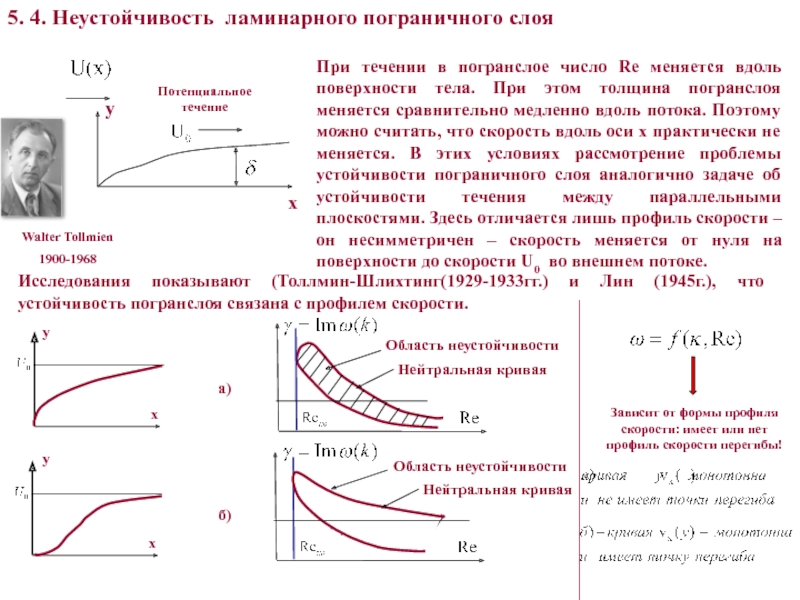
При течении в погранслое
число Re меняется вдоль поверхности тела. При этом толщина погранслоя
меняется сравнительно медленно вдоль потока. Поэтому можно считать, что скорость вдоль оси x практически не меняется. В этих условиях рассмотрение проблемы устойчивости пограничного слоя аналогично задаче об устойчивости течения между параллельными плоскостями. Здесь отличается лишь профиль скорости – он несимметричен – скорость меняется от нуля на поверхности до скорости U0 во внешнем потоке.Исследования показывают (Толлмин-Шлихтинг(1929-1933гг.) и Лин (1945г.), что устойчивость погранслоя связана с профилем скорости.
у
x
x
Область неустойчивости
Нейтральная кривая
Область неустойчивости
Нейтральная кривая
Зависит от формы профиля скорости: имеет или нет профиль скорости перегибы!
a)
б)
Walter Tollmien
1900-1968
у
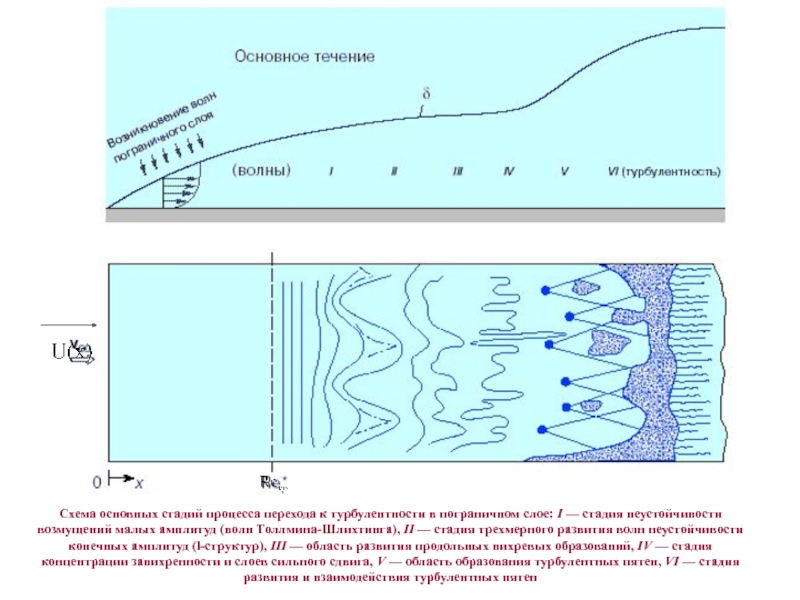
Слайд 20Схема основных стадий процесса перехода к турбулентности в пограничном слое:
I — стадия неустойчивости возмущений малых амплитуд (волн Толлмина-Шлихтинга), II
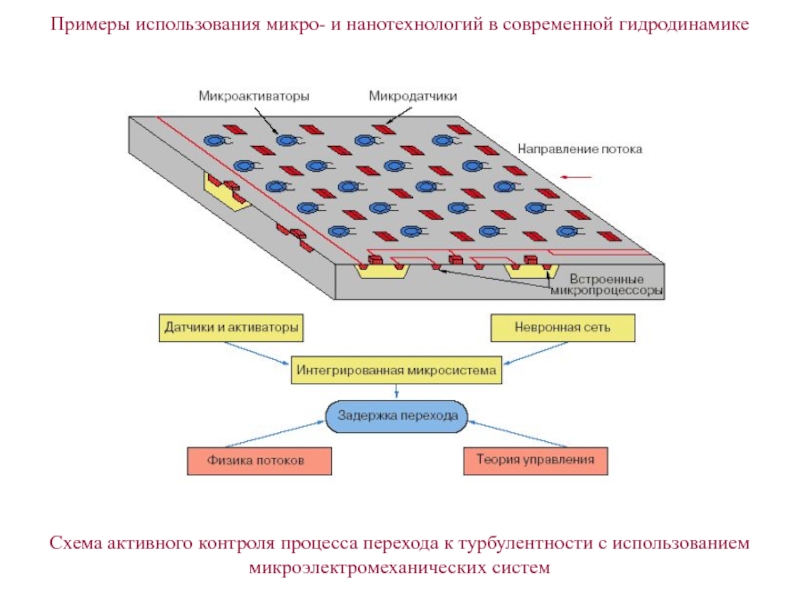
— стадия трехмерного развития волн неустойчивости конечных амплитуд (l-структур), III — область развития продольных вихревых образований, IV — стадия концентрации завихренности и слоев сильного сдвига, V — область образования турбулентных пятен, VI — стадия развития и взаимодействия турбулентных пятенСлайд 21Схема активного контроля процесса перехода к турбулентности с использованием микроэлектромеханических
систем
Примеры использования микро- и нанотехнологий в современной гидродинамике
Слайд 22
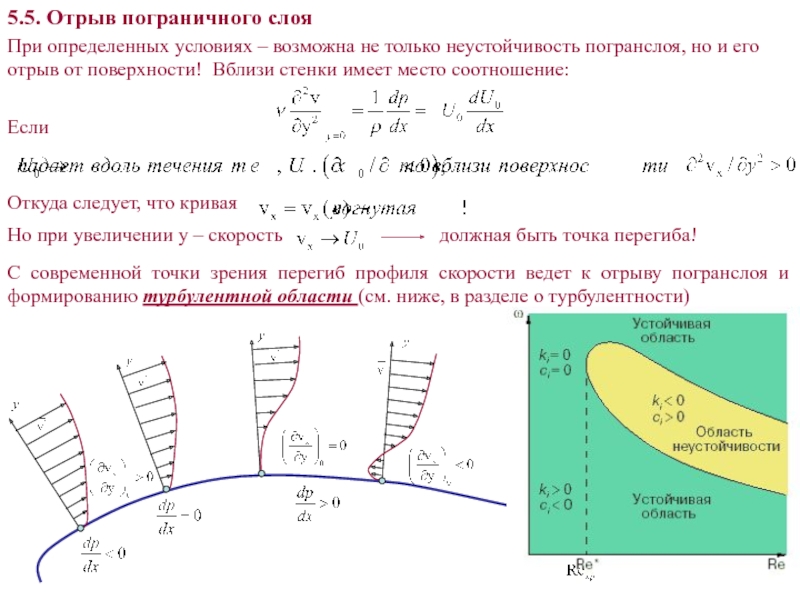
При определенных условиях – возможна не только неустойчивость погранслоя, но
и его отрыв от поверхности! Вблизи стенки имеет место соотношение:
Если
Откуда
следует, что криваяНо при увеличении y – скорость
должная быть точка перегиба!
5.5. Отрыв пограничного слоя
С современной точки зрения перегиб профиля скорости ведет к отрыву погранслоя и формированию турбулентной области (см. ниже, в разделе о турбулентности)
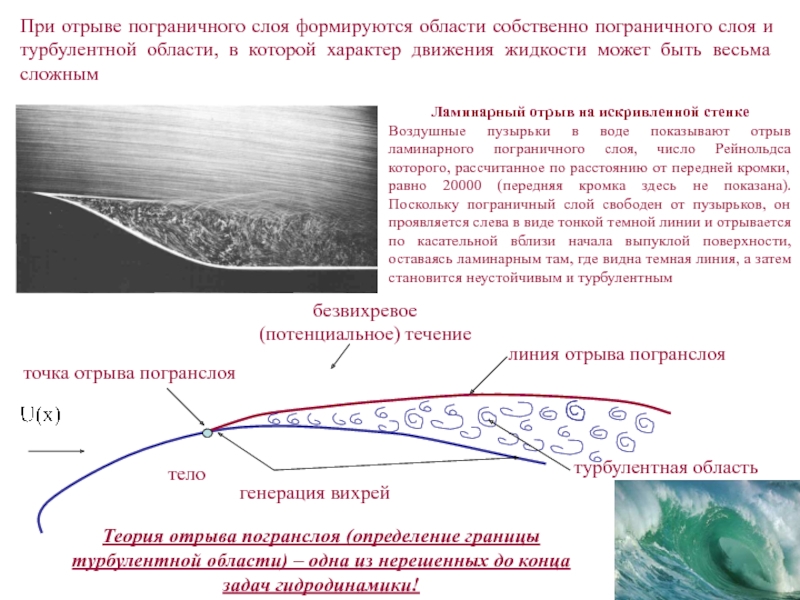
Слайд 23Ламинарный отрыв на искривленной стенке
Воздушные пузырьки в воде показывают отрыв
ламинарного пограничного слоя, число Рейнольдса которого, рассчитанное по расстоянию от
передней кромки, равно 20000 (передняя кромка здесь не показана). Поскольку пограничный слой свободен от пузырьков, он проявляется слева в виде тонкой темной линии и отрывается по касательной вблизи начала выпуклой поверхности, оставаясь ламинарным там, где видна темная линия, а затем становится неустойчивым и турбулентнымлиния отрыва погранслоя
точка отрыва погранслоя
турбулентная область
тело
При отрыве пограничного слоя формируются области собственно пограничного слоя и турбулентной области, в которой характер движения жидкости может быть весьма сложным
безвихревое (потенциальное) течение
генерация вихрей
Теория отрыва погранслоя (определение границы турбулентной области) – одна из нерешенных до конца задач гидродинамики!