Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
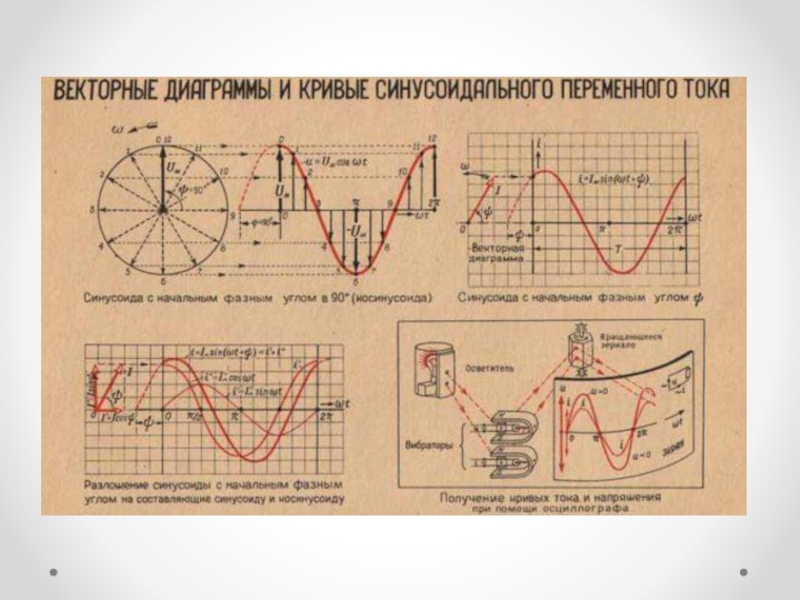
Векторная диаграмма токов и напряжений
Содержание
- 1. Векторная диаграмма токов и напряжений
- 2. В целом, для лучшего понимания процедур, происходящих
- 3. Слайд 3
- 4. Разновидности векторных диаграмм Любую характеристику электротехнической цепи,
- 5. Векторной диаграммой принято называть множество положительно направленных
- 6. Векторные диаграммы токов и напряжений визуально отображают
- 7. Круговая диаграмма, представляющая собой графическую гистограмму, образованную
- 8. Построение векторной диаграммы напряжений и токовДля лучшего
- 9. Согласно схемы цепи, изображенной на картинке а:
- 10. Суммарное входное напряжение, в соответствии со вторым
- 11. Поскольку конденсатору в цепи с электротоком, изменяющимся
- 12. RL=XL=ωL; UL=Im*RL*cos(ωt+π/2), где: RL – сопротивление катушки
- 13. Векторная диаграмма токов и напряжений RLC цепочке Источник: https://elquanta.ru/teoriya/vektornaya-diagramma-tokov-i-napryazhenijj.html
- 14. После простых преобразований по постулату Ома, уравнение
- 15. Скачать презентанцию
В целом, для лучшего понимания процедур, происходящих в радиотехнических цепях, их взаимосвязи между собой, бывает недостаточно оперировать характеристиками и параметрами данной цепи, имеющими цифровое отображение. В связи с тем, что основная
Слайды и текст этой презентации
Слайд 4Разновидности векторных диаграмм
Любую характеристику электротехнической цепи, изменяющуюся по синусоидальному или
косинусоидальному принципу, можно отобразить посредством точки на поверхности, в соответствующей
системе величин. В качестве размерности по оси Х выступает действительный компонент параметра, по оси Y размещается воображаемая составляющая. Именно такие составляющие входят в алгебраическую модель записи комплексной величины. Последующее соединение точки на поверхности и нулевой точки системы координат позволит рассматривать эту прямую и ее угол с действительной осью как изображение комплексного числа. На практике положительно направленный отрезок принято называть векторомСлайд 5Векторной диаграммой принято называть множество положительно направленных отрезков на комплексной
поверхности, которая соответствует комплексным значениям и параметрам гальванической цепи и
их взаимосвязям. По своему характеру векторные диаграммы подразделяются на:Точные гистограммы;
Качественные гистограммы.
Особенностями достоверных гистограмм является соблюдение пропорций всех характеристик и параметров, полученных путем вычислений. Данные диаграммы находят свое применение в проверке ранее проведенных расчетов. В основе использования качественных гистограмм лежит учет взаимного влияния характеристик друг на друга, и в основном они предшествуют расчетам либо заменяют их.
Слайд 6Векторные диаграммы токов и напряжений визуально отображают процесс достижения цели
по расчету электротехнической цепи. При соблюдении всех правил по построению
векторных отрезков можно просто из гистограммы установить фазы и амплитуды вещественных характеристик. Построение качественных гистограмм поможет контролировать правильный процесс решения задачи и с легкостью определить сектор с определяемыми векторами. В зависимости от особенностей построения, графические диаграммы делятся на такие типы:Слайд 7Круговая диаграмма, представляющая собой графическую гистограмму, образованную вектором, описывающим своим
концом круг или полукруг, при любых изменениях характеристик цепи;
Линейная
диаграмма, представляющая собой графический рисунок в виде прямой линии, образованной вектором, посредством изменения характеристик цепи.
Слайд 8Построение векторной диаграммы напряжений и токов
Для лучшего понимания того, как
построить векторную диаграмму токов и напряжений, следует рассматривать RLC цепь,
состоящую из пассивного элемента в виде резистора и реактивных элементов в виде катушки индуктивности и конденсатора.Слайд 9Согласно схемы цепи, изображенной на картинке а: U – величина
переменного напряжения в текущий момент времени; I – мощность тока
в заданный момент времени; UА – напряжение, падающее на активном сопротивлении; UC – напряжение, падающее на емкостной нагрузке; UL – напряжение, падающее на индуктивной нагрузке. Поскольку входное напряжение U изменяется по колебательному закону, то сила тока характеризуется уравнением: I=Im*cosωt, где: Im – максимальная амплитуда тока; ω – частота тока; t – время.Слайд 10Суммарное входное напряжение, в соответствии со вторым законом Кирхгофа, равно
общей величине напряжений на всех элементах цепи: U=UC+UL+UA.
В соответствии
с законом Ома, падение напряжения на резистивном компоненте равняется: UA= Im*R*cosωt.
Слайд 11Поскольку конденсатору в цепи с электротоком, изменяющимся по синусоиде, свойственно
наличие реактивного емкостного сопротивления, и ввиду того, что напряжение на
нем постоянно имеет фазовое отставание от протекающего тока на π/2, то уместно выражение: RC=XC=1/ωC;UC=Im*RС*cos(ωt-π/2), где:
RC – сопротивление конденсатора;
XC – реактивный импеданс конденсатора;
C – емкость конденсатора
Слайд 12RL=XL=ωL;
UL=Im*RL*cos(ωt+π/2), где:
RL – сопротивление катушки индуктивности;
XL –
реактивный импеданс катушки индуктивности;
L – индуктивность катушки.
Следовательно, общее
напряжение, подведенное к цепи, выглядит: U=Um*cos(ωt±φ), где:
Um – максимальная величина напряжения; φ – фазовый сдвиг.