Слайд 1Вхідний контроль:
Записати формули для визначення характеристик фазового складу грунту: щільності
грунту, щільності частинок грунту, вологості.
Методи визначення зернового складу.
Назвати характерні вологості
грунту.
У якого грунту число пластичності більше: у суглинка чи супіску?
Що більше: щільність грунту чи щільність частинок грунту?
Інформація за результатами наукової роботи.
Слайд 2Лекція №8
МЕХАНІКА ГРУНТІВ
Грунт як деформоване тверде тіло
Слайд 3ПЛАН
Про механіку ґрунтів
Поняття про навантаження, напруження, переміщення та деформації
Деформаційні
характеристики ґрунту
Слайд 41. Про механіку ґрунтів
В розділі “Грунтознавство” вивчали походження різних
ґрунтів, їх фізичні і будівельні властивості.
В розділі “Механіка ґрунтів” вивчаються
механічні властивості грунтів, методи визначення напружень і деформацій в грунтових масивах, а також методи розрахунку ґрунтових масивів на міцність та стійкість.
Механічними прийнято називати властивості, які характеризують поведінку грунту під дією навантаження.
Слайд 52. Поняття про навантаження, напруження, переміщення та деформації
Навантаження
На ґрунтовий
масив діють тривалі і короткочасні навантаження.
Тривалі (тривалістю від 102с до
102 років) :
від власної ваги розташованого вище ґрунту;
від ваги споруд, які опираються на ґрунт.
Слайд 6Короткочасні (тривалістю від 10-3с до 10 с):
від проїзду автомобілів, поїздів,
літаків;
від вібрації двигунів, генераторів, машин в приміщеннях.
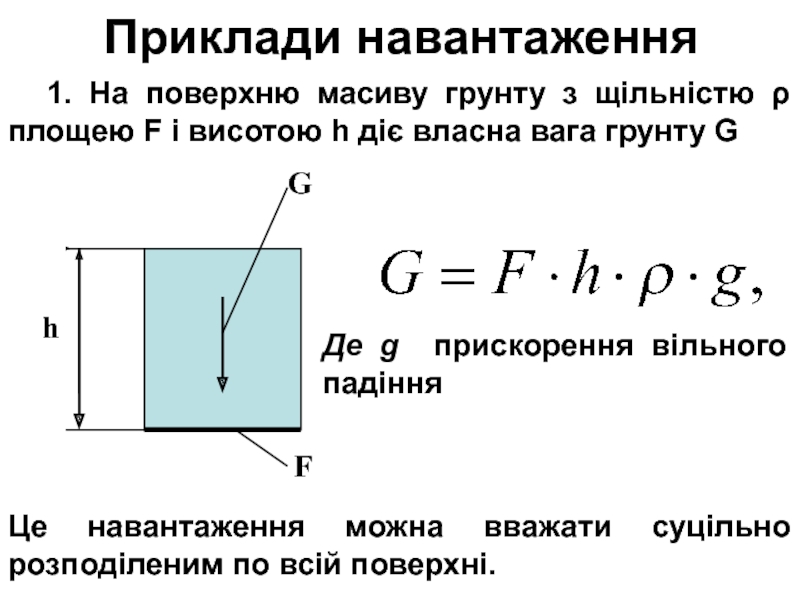
Слайд 7Приклади навантаження
1. На поверхню масиву грунту з щільністю ρ площею
F і висотою h діє власна вага грунту G
Це
навантаження можна вважати суцільно розподіленим по всій поверхні.
Де g прискорення вільного падіння
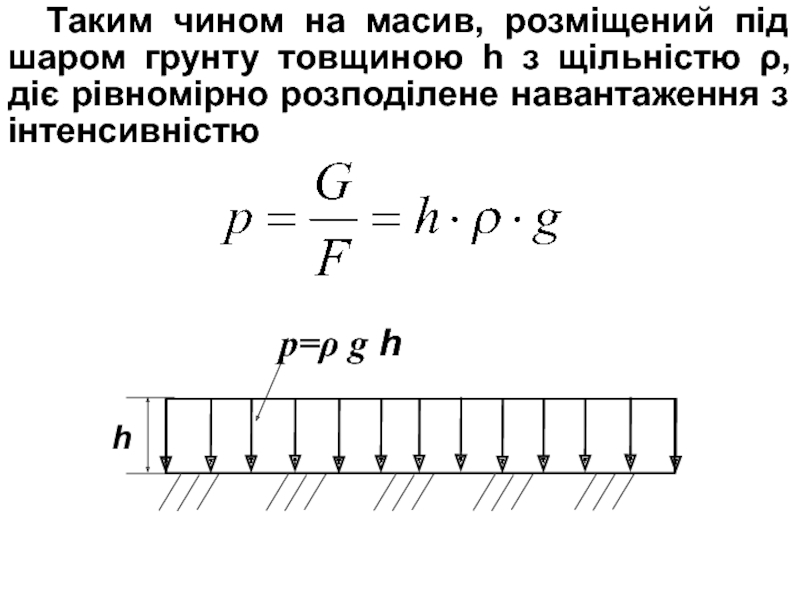
Слайд 8Таким чином на масив, розміщений під шаром грунту товщиною h
з щільністю ρ, діє рівномірно розподілене навантаження з інтенсивністю
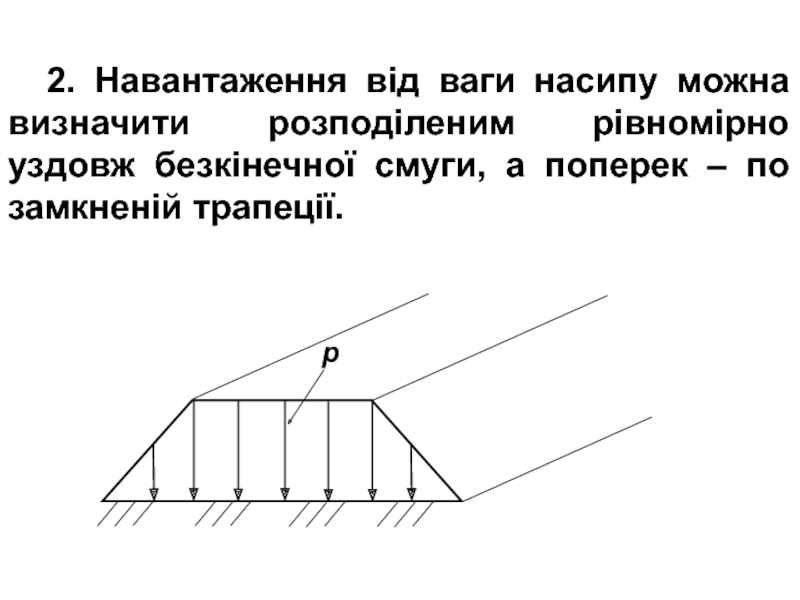
Слайд 92. Навантаження від ваги насипу можна визначити розподіленим рівномірно уздовж
безкінечної смуги, а поперек – по замкненій трапеції.
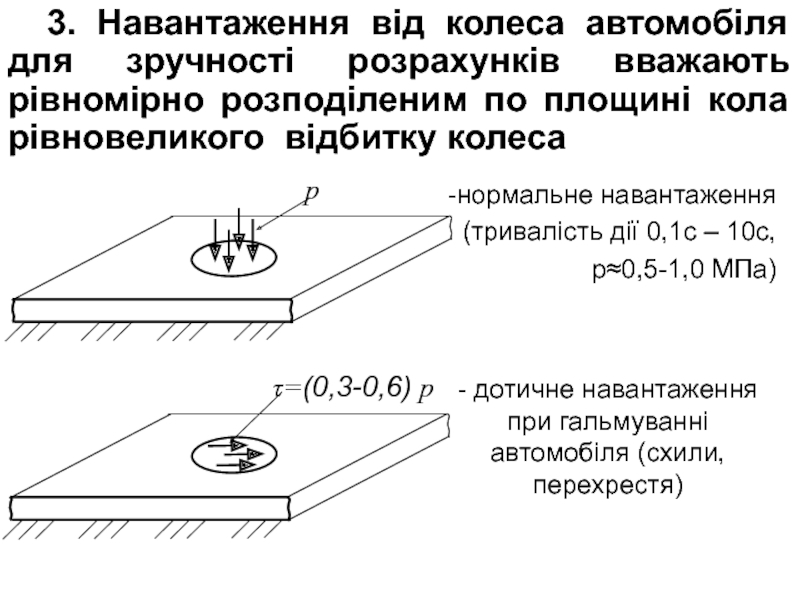
Слайд 10 -нормальне навантаження
(тривалість дії 0,1с – 10с,
р≈0,5-1,0 МПа)
- дотичне навантаження при гальмуванні автомобіля (схили, перехрестя)
3. Навантаження від
колеса автомобіля для зручності розрахунків вважають рівномірно розподіленим по площині кола рівновеликого відбитку колеса
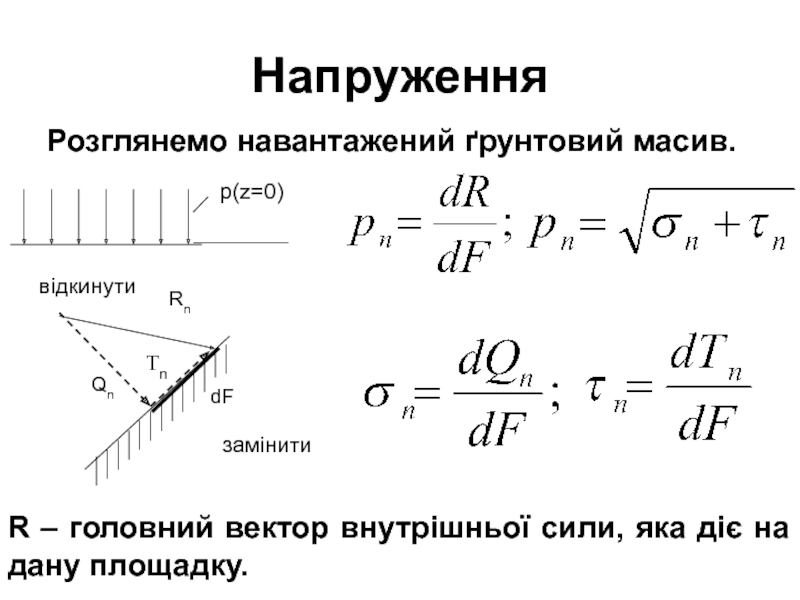
Слайд 11Напруження
Розглянемо навантажений ґрунтовий масив.
R – головний вектор внутрішньої сили,
яка діє на дану площадку.
Слайд 12Якщо через деяку точку ґрунтового масиву, на поверхні якого діє
навантаження р(z=0), провести довільну площину n і відкинути уявно всю
частину масиву по один бік цієї площини, то потрібно замінити дію відкинутої частини на частину що залишилась - відповідною силою R. Внутрішня сила (рn), яка приходиться на одиницю площі (Fn), називається напруженням.
Головний вектор напружень рn зручно розкласти на складові: σn–нормальне напруження та tn – дотичне напруження.
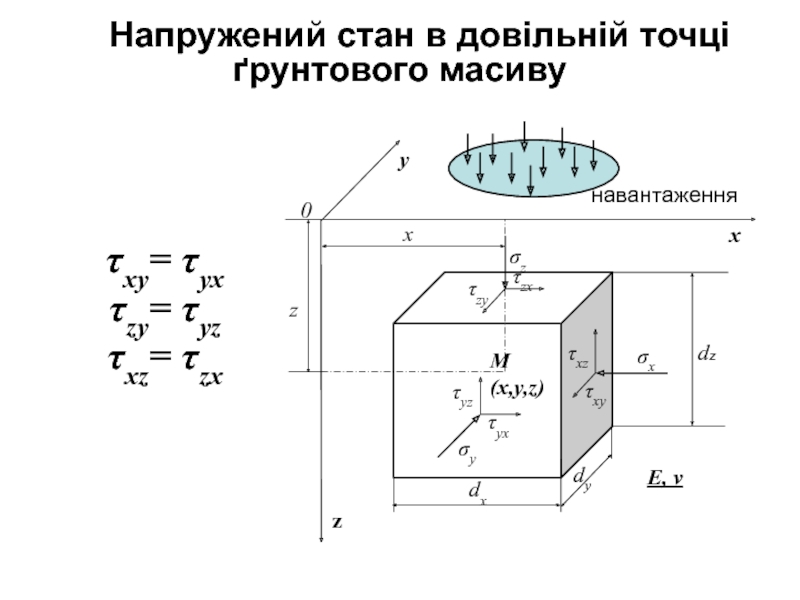
Слайд 13Напружений стан в довільній точці ґрунтового масиву
τxy= τyx
τzy= τyz
τxz= τzx
Слайд 14Щоб охарактеризувати напружений стан в довільній точці М(x,y,z) ґрунтового масиву,
розміщують початок декартових координат (0) в деякій точці поверхні масиву,
виділяють поблизу точки М елементарний паралелепіпед з ребрами dx,dy,dz і позначають σx – вертикальне нормальне напруження. σy,σz–горизонтальні нормальні напруження. t zу, t уz однакові між собою по закону “парності” дотичних напружень, які діють по гранях паралельних осі Х; t zx, t xz – те ж, паралельних осі У; t xy, t yx– те ж, паралельних осі Z.
Слайд 15Враховуючи попарну рівність дотичних напружень, для повної характеристики напруженого стану
необхідно знайти 3 нормальні і три дотичні компоненти напружень. Вони
повинні бути встановлені, як функції координат точки, в якій визначаються напруження і як функція величин, які характеризують навантаження і матеріал масиву.
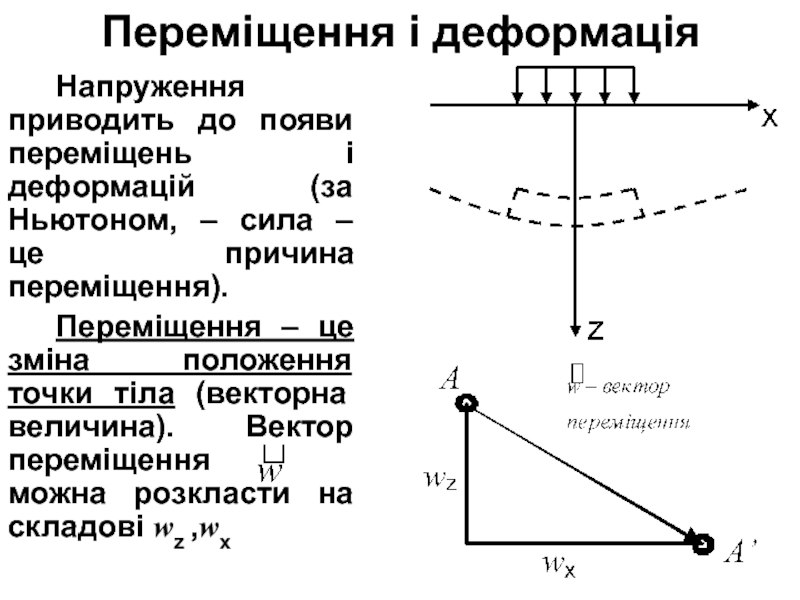
Слайд 16Переміщення і деформація
Напруження приводить до появи переміщень і деформацій (за
Ньютоном, – сила – це причина переміщення).
Переміщення – це зміна
положення точки тіла (векторна величина). Вектор переміщення можна розкласти на складові wz ,wх
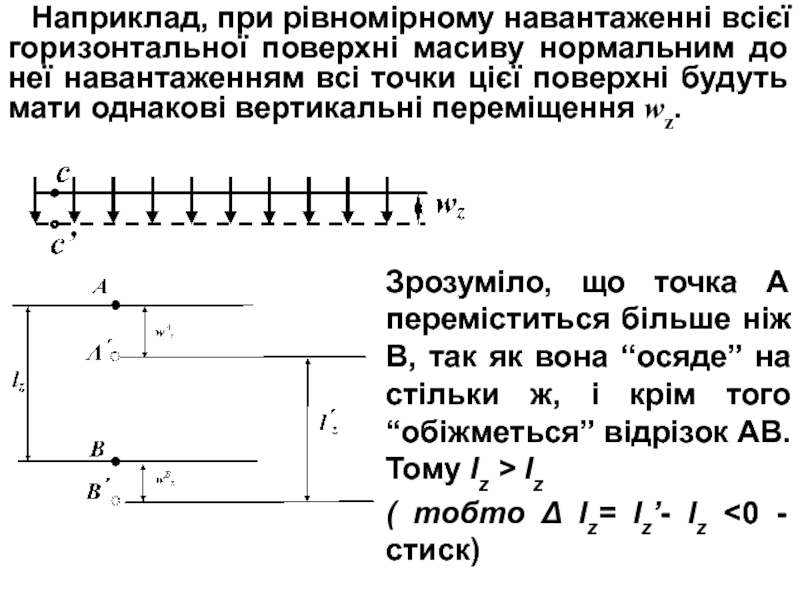
Слайд 17Наприклад, при рівномірному навантаженні всієї горизонтальної поверхні масиву нормальним до
неї навантаженням всі точки цієї поверхні будуть мати однакові вертикальні
переміщення wz.
Зрозуміло, що точка А переміститься більше ніж В, так як вона “осяде” на стільки ж, і крім того “обіжметься” відрізок АВ. Тому lz > lz
( тобто Δ lz= lz’- lz <0 - стиск)
Слайд 18Деформація– це зміна положення точок тіла відносно одна одній. Деформація
буквально – зміна форми). Наприклад, при рівномірному навантаженні всієї поверхні
масиву відстань між т.А і т.В змінилась на
– абсолютна деформація.
Відношення – відносна
деформація в напрямку осі z.
Слайд 19Деформації і переміщення грунту зумовлені такими процесами:
обтиснення частинок і
їх агрегатів;
зменшення оболонки зв’язаної води в зоні контакту при наближенні
частинок;
обтиснення порової води та повітряних бульбашок;
руйнування агрегатів із частинок що склеїлись і руйнування окремих частинок;
видавлювання вільної води із пор;
перепакування зерен шляхом взаємного переміщення.
Слайд 20Переміщення і деформації, зумовлені першими трьома процесами, оборотні пружні (elastic)
тобто вони зникають після розвантаження, а зумовлені останніми трьома процесами
– не оборотні (рlastic) тобто вони залишаються після розвантаження. Тому повне переміщення і повна відносна деформація складаються із пружної (е) і залишкової частин (р) :
Слайд 213. Деформаційні характеристики ґрунту
Механічні властивості ґрунту, які характеризують його поведінку
під дією навантаження, поділяються на дві групи: деформаційні та міцнісні.
Деформаційні характеристики визначають здатність ґрунтового масиву змінювати розміри і форму під дією навантаження. Міцнісні визначають здатність ґрунту протистояти дії навантажень.
До деформаційних характеристик відносяться: модуль пружності, модуль деформації, коефіцієнт пружної поперечної деформації, коефіцієнт поперечної деформації, а також коефіцієнт стисливості, просідання, консолідації.
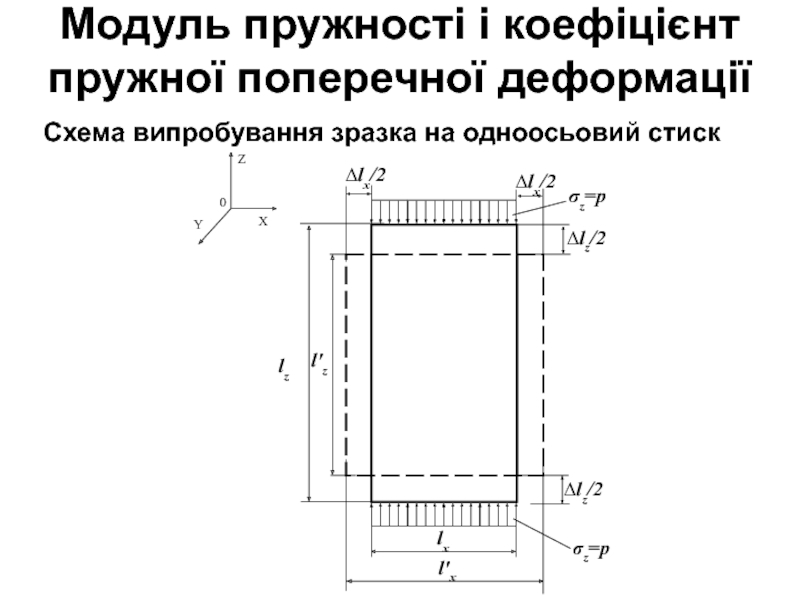
Слайд 22Схема випробування зразка на одноосьовий стиск
Модуль пружності і коефіцієнт
пружної поперечної деформації
Слайд 23При випробуванні грунту на одноосьове стискування нормальне напруження σz викликає
зменшення поздовжнього розміру Іz до Іz' й збільшення поперечного розміру
ІХ до ІХ'.
Як відомо, абсолютною поздовжньою деформацією є різниця:
абсолютною поперечною:
відносною
поздовжньою:
відносною
поперечною:
.
Слайд 24Якщо залишкова деформація відсутня, то повна деформація рівна пружній
.
Досвід показав, що в цьому випадку тобто при повністю оборотній
деформації для багатьох матеріалів справедливий закон Гука (Р.Гук –1660р) :
поздовжня відносна деформація пропорційна напруженню, що її викликало
Слайд 25Постійна Ее – називається модулем пружності (модулем Юнга) і є
важливою деформаційною характеристикою пружніх властивостей матеріалу.
Із закону Гука випливає, що
модулем пружності є відношення поздовжнього нормального напруження до викликаної ним повздовжньої відносної пружної деформації в умовах одновісного напруженого стану :
.
Слайд 26Приклади типових значеннь модуля пружності Ее:
сталь - 200000 МПа,
бетон –
30000 МПа,
оргскло – 3000 МПа,
пісок – 100 МПа,
супісок і глина
в пластичному стані –20-100 МПа.
Слайд 27
де : νе – постійна, яка називається коефіцієнтом пружної
поперечної деформації (коефіцієнт Пуассона, 1892р).
Коефіцієнтом Пуассона називається взяте з
від’ємним знаком відношення поперечної до поздовжньої відносних пружніх деформацій в умовах одновісного напруженого стану
Поздовжня і поперечна пружні деформації також пов’язані одна з одною:
Слайд 28Типові значення νе :
сталь – 0,3,
бетон – 0,16,
пісок –
0,25,
супісок і суглинок в пластичному стані – 0,35.
Для ідеального пружнього
тіла Ее ,νе – повний набір констант в тому розумінні, що вони дають всю інформацію про властивості тіла, необхідних для визначення виникаючих в ньому напружень, переміщень, деформацій при різних навантаженнях.
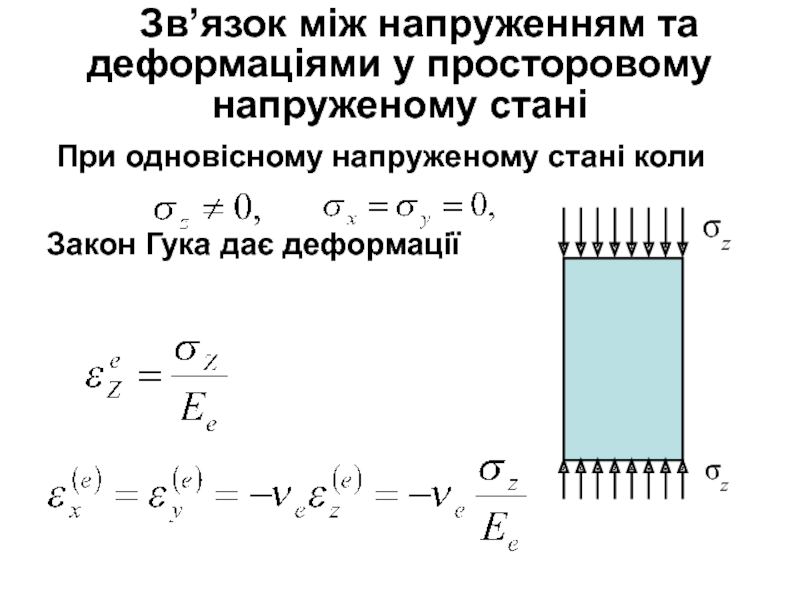
Слайд 29Зв’язок між напруженням та деформаціями у просторовому напруженому стані
При одновісному
напруженому стані коли
Закон Гука дає деформації
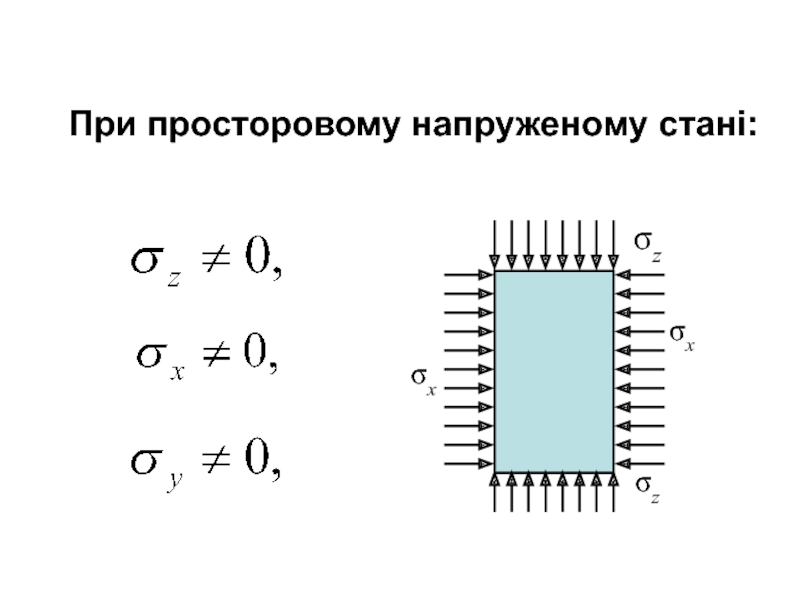
Слайд 30При просторовому напруженому стані:
Слайд 31В трьохвимірному напруженому стані залежність між напруженнями та пружними відносними
деформаціями відображається трьома рівняннями закону Гука (відносні деформації визначаються додаванням
виходячи з незалежності дії сил):
Слайд 32За допомогою цих залежностей розв’язані різноманітні задачі про напружено-деформаційний стан
суцільного середовища і розроблений потужний апарат розрахунку.