Внутреннее трение (вязкость) жидкости. Уравнение Ньютона. Ньютоновские

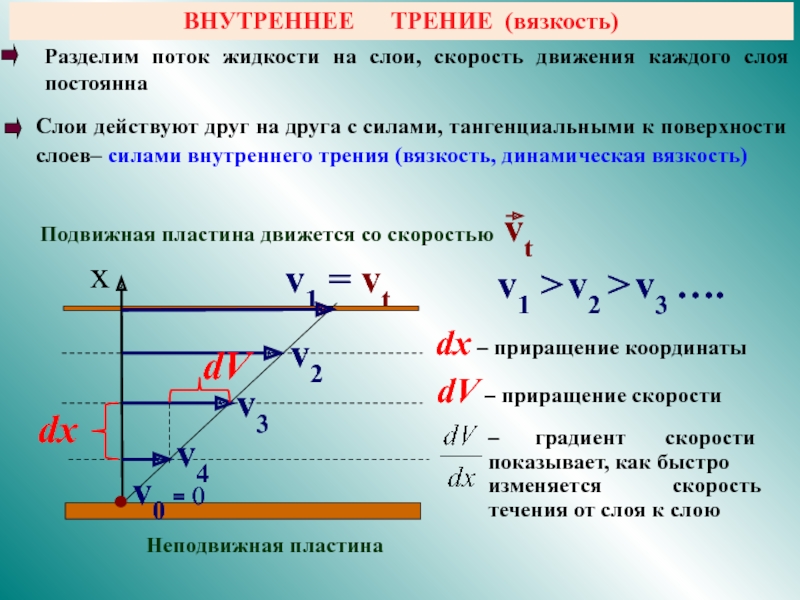
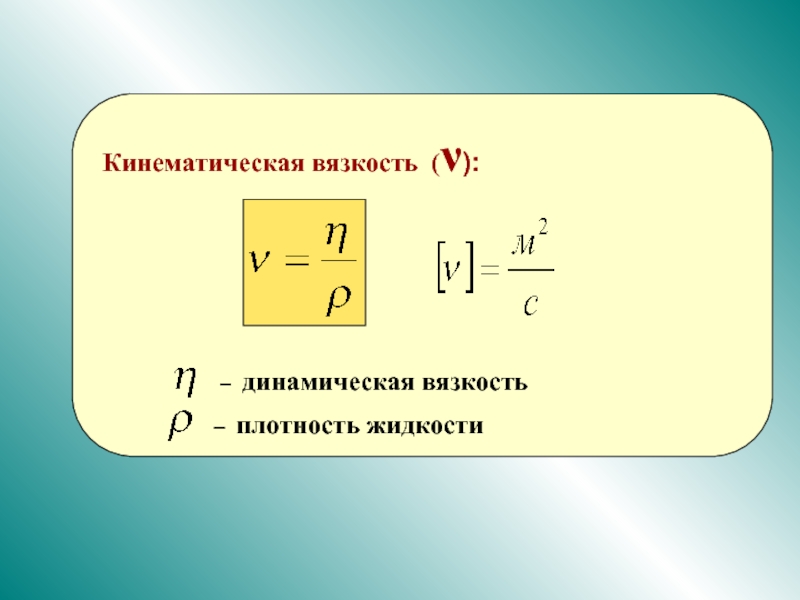
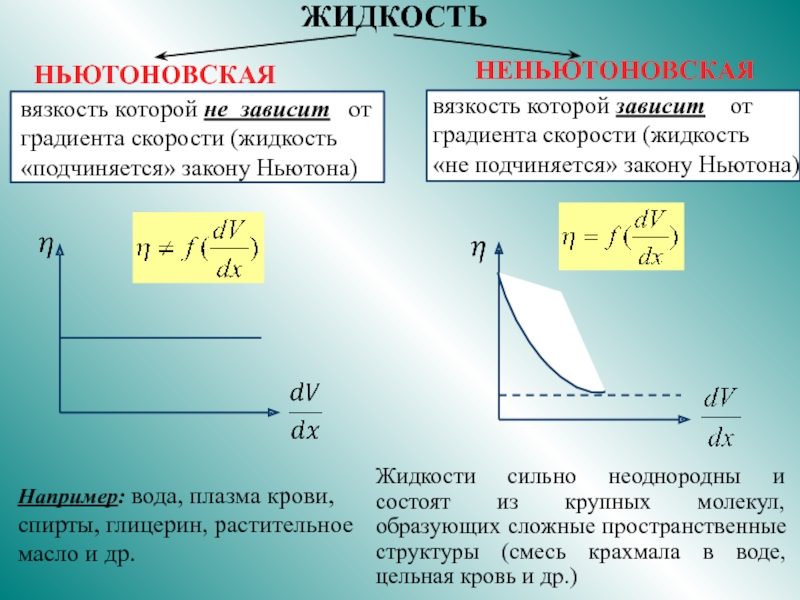
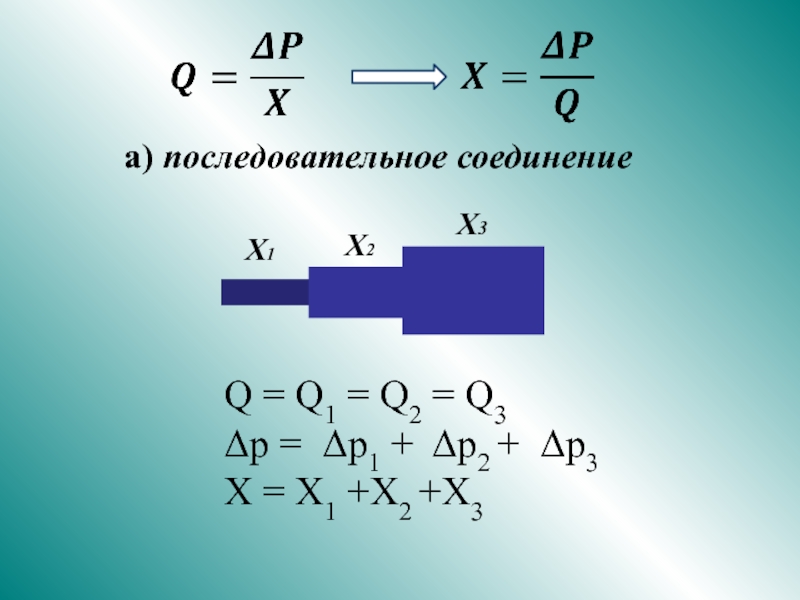
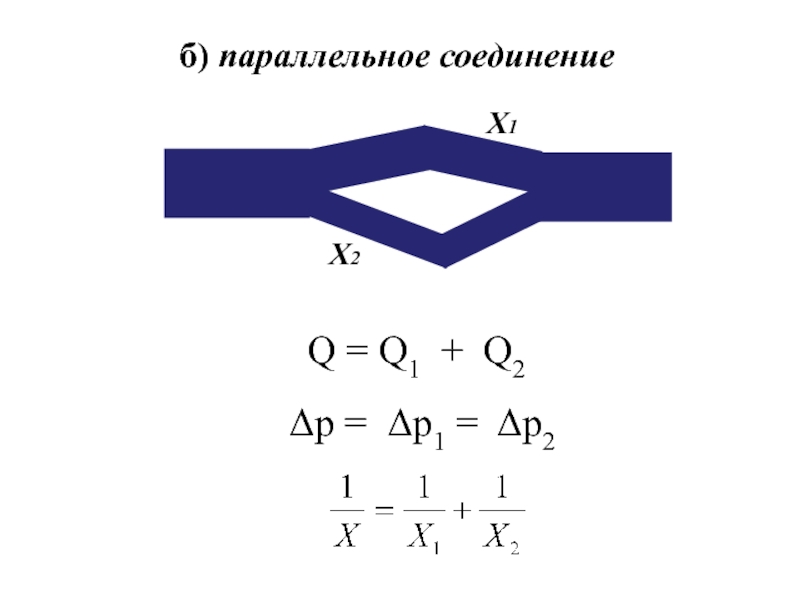
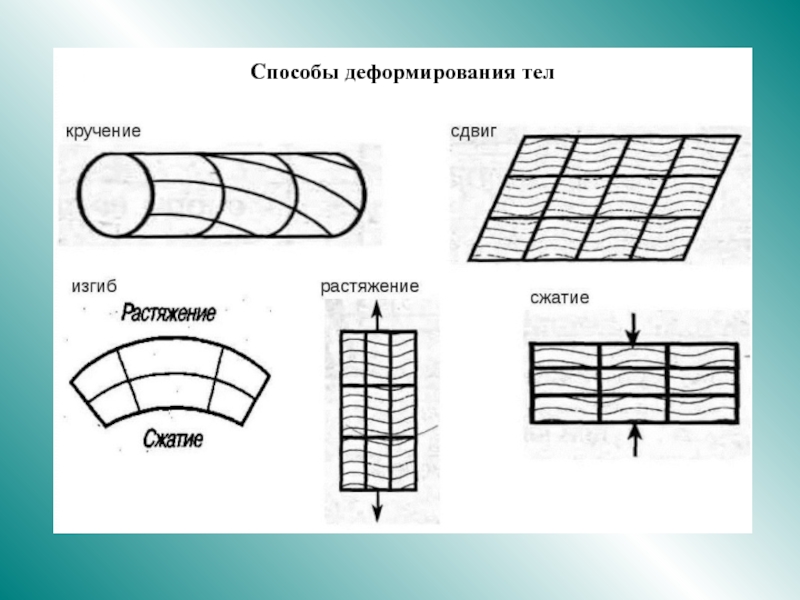
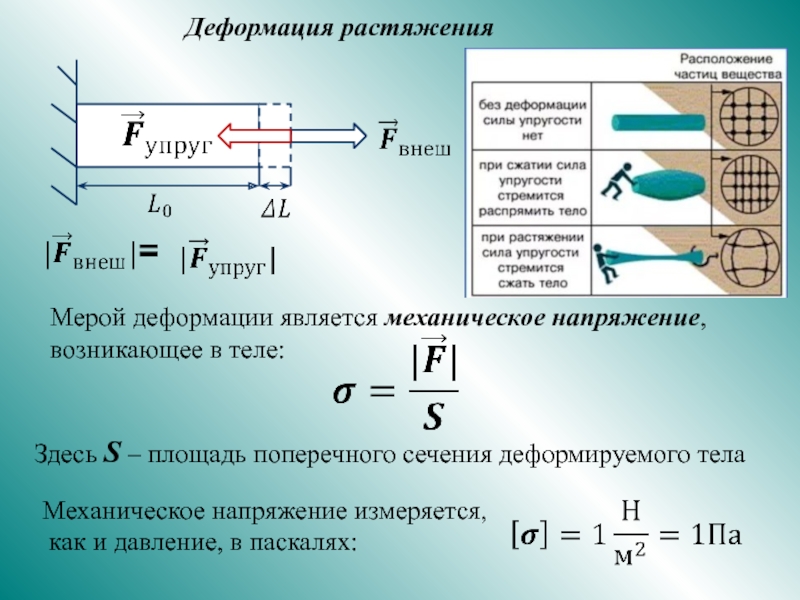
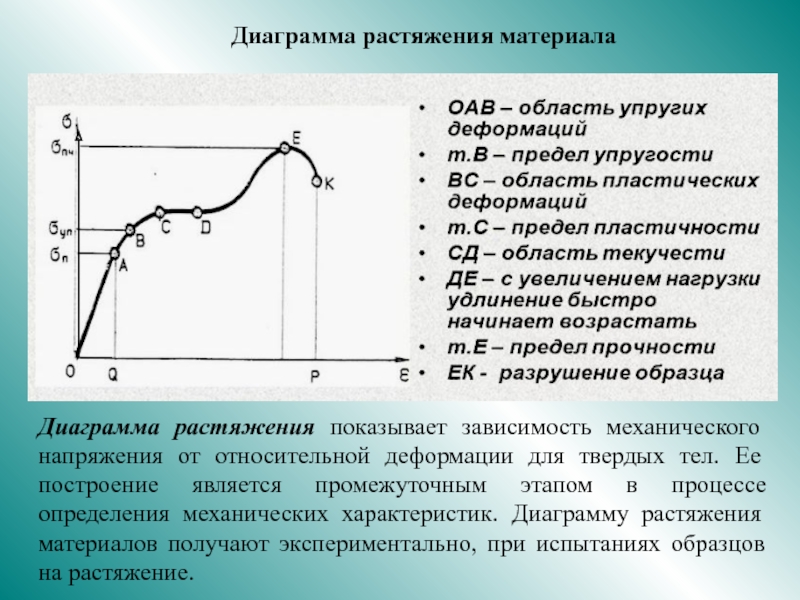
и
неньютоновские жидкости.
2. Ламинарное и турбулентное течение.

Число
Рейнольдса.
3. Течение жидкостей по трубам. Формула Пуазейля.
Гидравлическое сопротивление.
4. Методы измерения вязкости жидкости.

Тема 1: ТЕЧЕНИЕ И СВОЙСТВА ЖИДКОСТЕЙ

ОСНОВЫ РЕОЛОГИИ
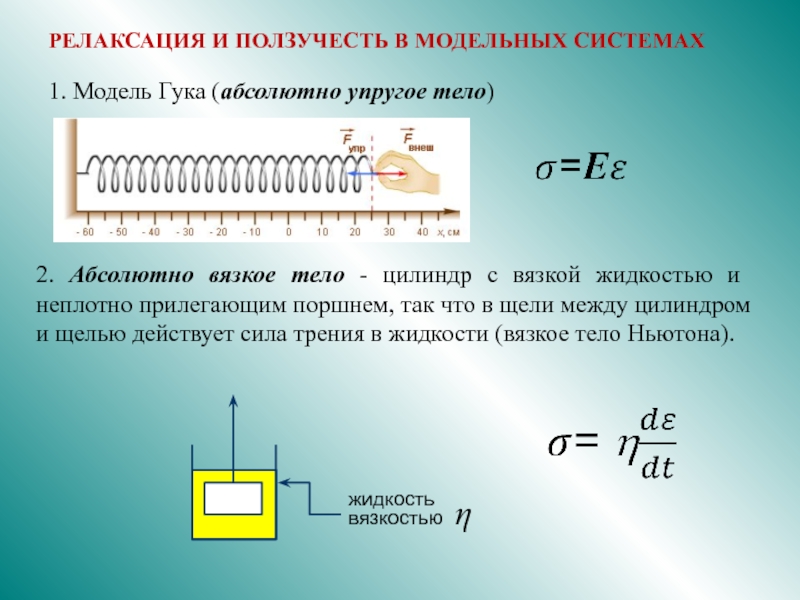
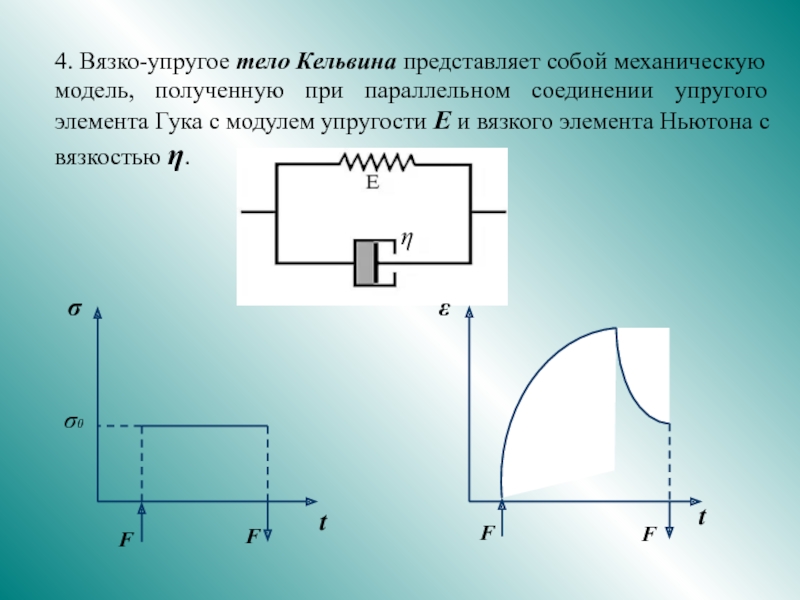
Реология – раздел физики, изучающий текучесть вещества и деформации

слоев– силами внутреннего трения (вязкость, динамическая вязкость)
ВНУТРЕННЕЕ ТРЕНИЕ

(вязкость)

Разделим поток жидкости на слои, скорость движения каждого слоя постоянна

S –площадь соприкосновения слоев
Исаак Ньютон

 (мПa.с)
воздух 0.018
вода (0 °C) 1.8
вода (20 °C) 1.0
вода (100 °C) ~ 0.3
кровь (мужчины, норма (37 °C) 4.3-5.3
кровь (женщины, норма (37 °C) 3.9-4.9
плазма крови, норма (37 °C) ~1.5
кровь, диабет (37°C) ~ 23
кровь, туберкулез (37°C) ~ 1.0

h Зависит от молекулярной структуры

сильно неоднородны и состоят из крупных молекул, образующих сложные пространственные

структуры (смесь крахмала в воде, цельная кровь и др.)

слоёв), при этом скорость частиц в каждом слое остаётся постоянной
ТУРБУЛЕНТНОЕ

ТЕЧЕНИЕ

– течение, сопровождающееся хаотическими движениями жидкости – завихрениями, при этом скорость частиц в каждом слое не постоянная, всё время изменяется.
Турбулентное течение жидкости сопровождается шумом.

Режимы течения жидкости. Число Рейнольдса.

Рейнольдса
Для контроля за характером течения

при помощи капилляра впускают ту же, но окрашенную жидкость во входное сечение трубки

При малых скоростях подкрашенная жидкость текла ровной, строго очерченной струйкой по всей длине трубы (течение ламинарное).

установил, что переход от ламинарного течения жидкости к турбулентному происходила

в зависимости от:
D – диаметра трубы;
V – скорости течения жидкости;
ρ – плотности жидкости;
η – динамической вязкости жидкости.

число Рейнольса – Re

КИНЕМАТИЧЕСКАЯ ВЯЗКОСТЬ

котором происходит переход
ламинарного течения в турбулентное
Для

гладких цилиндрических труб
Re кр ≈ 2300

Если

, то течение турбулентное

Если для данной жидкости, в данной трубе Re ‹ Re кр ,
то течение будет ламинарным

по трубам (или сосудам) имеет вид параболы
– слои, прилипшие к

стенкам, не движутся;

– слои вдоль оси трубы (в центре) двигаются с наибольшей скоростью;

– у промежуточных слоёв скорости убывают к краям трубы.

ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ ПО ТРУБЕ

единицу времени) в трубе равна:
ФОРМУЛА ПУАЗЕЙЛЯ

сечение линейного проводника за единицу времени
Q – объёмная скорость –

объём жидкости, протекающей через поперечное сечение трубы за единицу времени

U = (φ1 - φ2 ) – напряжение, т.е. разность потенциалов на концах проводника

P1 – P2 – разность давлений на концах трубы

R – электрическое сопротивление

X - гидравлическое сопротивление

чем электрическое из-за
существования пристеночных заторможенных слоев
По аналогии с электрическим

сопротивлением,
гидравлическое сопротивление можно
рассмотреть для соединения труб (сосудов)

= Δp1 + Δp2 + Δp3
Х = Х1 +Х2 +Х3

= Δp2

для измерения вязкости называется вискозиметром.

Рассмотрим следующие методы измерения вязкости жидкости:

Метод

Стокса (метод падающего шарика);

Метод Оствальда (капиллярный метод);

Ротационный метод.

(глицерин, различные масла и пр.) в случае, если есть достаточно

большой объем жидкости. Метод основан на измерении скорости падения шарика в исследуемой жидкости (см. лабораторную работу №7).

Капиллярные методы (метод Оствальда) –
основаны на применении формулы Пуазейля. В простейшем случае вискозиметр Оствальда представляет собой трубку с небольшой полой сферой фиксированного объема. Сравнивая время истечения из этого объема воды и исследуемой жидкости, определяют искомую вязкость (см. лабораторную работу №8).

только определять вязкость жидкости, но и зависимость вязкости от градиента

скорости (скорости сдвига). Однако для измерения вязкости необходимо иметь большой объем жидкости.
Вискозиметр имеет два цилиндра с общей осью вращения. Пространство между ними заполняется исследуемой жидкостью. При вращении наружного цилиндра внутренний поворачивается на некоторый угол, зависящий от вязкости жидкости.
В настоящее время существует множество модификаций метода.

Для ньютоновских жидкостей вязкость не зависит от скорости вращения цилиндра (градиента скорости).
Для неньютоновских жидкостей зависимость вязкости от скорости вращения можно определить количественно.

Гука. Модуль Юнга.

Кривая деформации.

Релаксация и ползучесть.

Модели упругого, вязкого

и вязкоупругих тел.

взаимного расположения частиц материальной среды,
которое приводит к искажению формы

и размеров тела

– площадь поперечного сечения деформируемого тела
Механическое напряжение измеряется,
как и

давление, в паскалях:

величиной относительного удлинения (относительной деформации):

Для небольших деформаций справедлив закон Гука:
Механическое напряжение, возникающее в теле при его деформации прямо пропорционально относительной деформации:

Здесь Е – модуль Юнга (модуль продольной упругости)

при упругой деформации. Назван в честь английского врача и физика

XIX века Томаса Юнга. Величина модуля Юнга зависит только от вида материала и не зависит от размеров и формы тела.

Модуль Юнга позывает механическое напряжение, которое нужно приложить к

телу, чтобы удлинить его в два раза. Для различных материалов модуль Юнга изменяется в широких пределах:

деформации для твердых тел. Ее построение является промежуточным этапом в

процессе определения механических характеристик. Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.

ползучести.

цилиндр с вязкой жидкостью и неплотно прилегающим поршнем, так что

в щели между цилиндром и щелью действует сила трения в жидкости (вязкое тело Ньютона).

1. Модель Гука (абсолютно упругое тело)

жидкость
вязкостью h

действием напряжения упруго деформируется и в то же время может

течь. Это одна из возможных моделей мягких биологических тканей. Представляет собой последовательно соединенные упругий и вязкий элементы:

s

t

F

F

e

t

F

F

параллельном соединении упругого элемента Гука с модулем упругости Е и

вязкого элемента Ньютона с вязкостью h.

h

e

t

F

F