Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ÚVOD DO TESTOVÁNÍ STATISTICKÝCH HYPOTÉZ
Содержание
- 1. ÚVOD DO TESTOVÁNÍ STATISTICKÝCH HYPOTÉZ
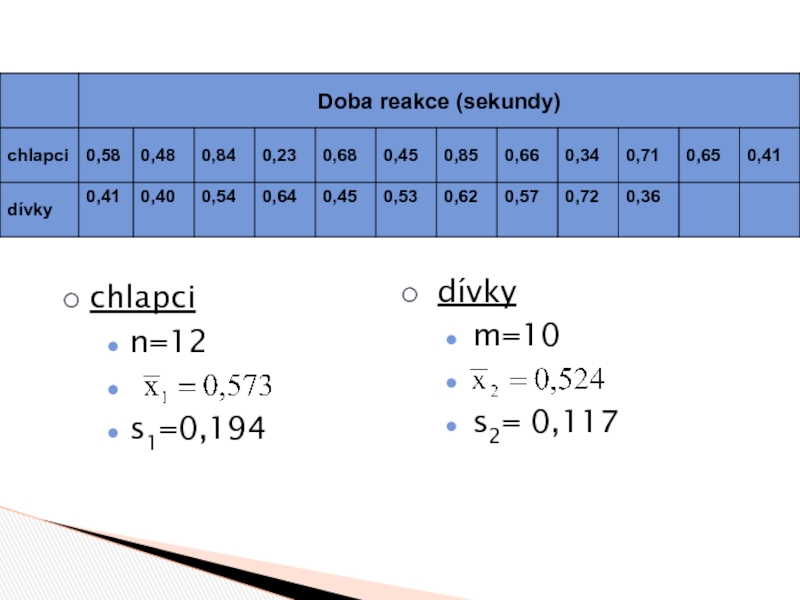
- 2. PříkladV rámci pokusu, který proběhl na univerzitě
- 3. chlapci n=12 s1=0,194dívkym=10 s2= 0,117
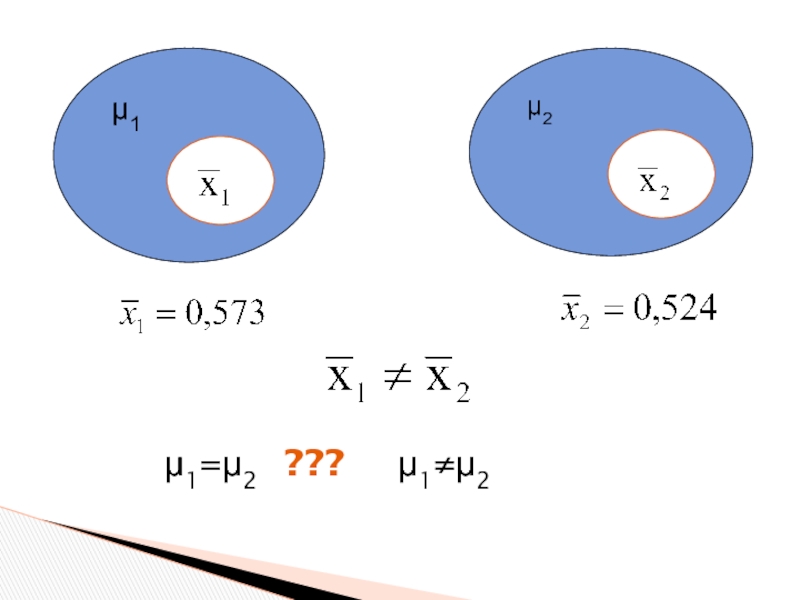
- 4. μ1μ2 μ1=μ2 ??? μ1≠μ2
- 5. Testování hypotézH0: μ1=μ2H1: μ1≠μ2H1: μ1>μ2H1: μ1
- 6. statistická hypotéza – tvrzení o parametrech rozdělení
- 7. Rozdělení testové statistiky T za předpokladu, že
- 8. Rozdělení testové statistiky T za předpokladu, že
- 9. Rozhodovací pravidlo (oboustranný test)Tα… kritická hodnota pro
- 10. Alternativní způsob (při využití statistického SW)rozhodnutí
- 11. chyba 1. druhuchyba 2. druhuzamítnutí správné nulové
- 12. realitaH0 platíH0 neplatízávěr testu (rozhodnutí)přijmout H0 zamítnout H0Při
- 13. Postup při statistickém testu1) Formulace nulové a
- 14. Скачать презентанцию
PříkladV rámci pokusu, který proběhl na univerzitě v Mississippi, byli studenti požádáni, aby reagovali na stimul v podobě rozsvícení červeného světla. Pokusu se zúčastnilo 12 chlapců a 10 dívek, pro
Слайды и текст этой презентации
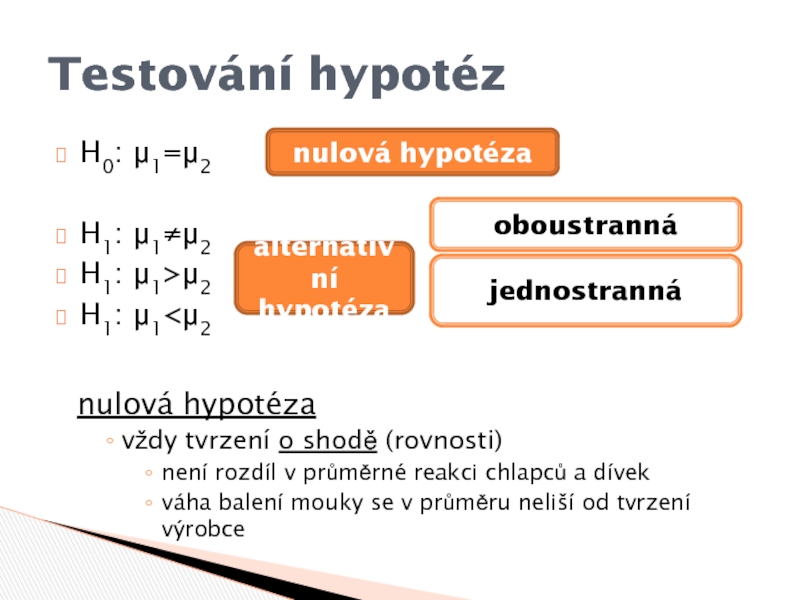
Слайд 5Testování hypotéz
H0: μ1=μ2
H1: μ1≠μ2
H1: μ1>μ2
H1: μ1
o shodě (rovnosti)
není rozdíl v průměrné reakci chlapců a dívek
váha
balení mouky se v průměru neliší od tvrzení výrobceСлайд 6statistická hypotéza – tvrzení o parametrech rozdělení nebo jeho tvaru
statistický
test
využití informace ve výběrových datech pro vyslovení závěru o
H0testová statistika (testové kriterium)
charakterizuje stupeň nesouladu mezi
tvrzením nulové hypotézy a pozorováním
(naměřenými daty)
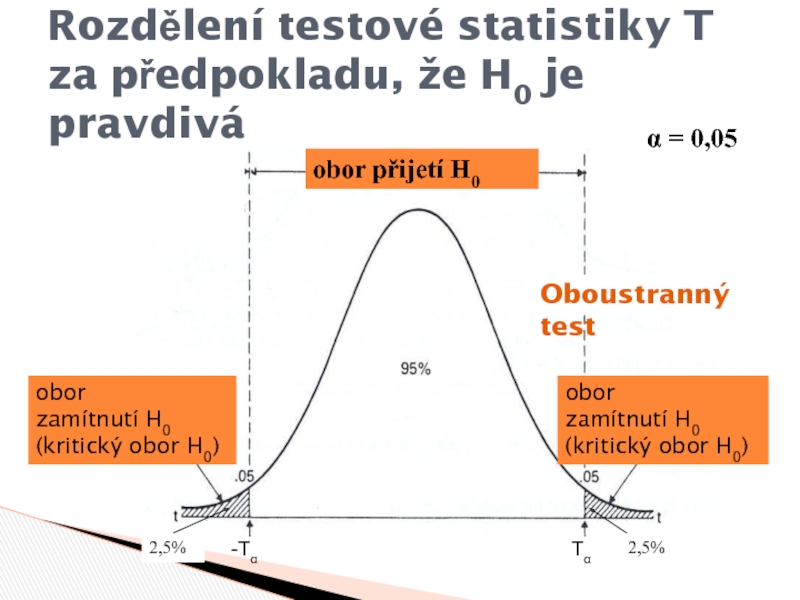
Слайд 7Rozdělení testové statistiky T za předpokladu, že H0 je pravdivá
Tα
-Tα
Oboustranný
test
2,5%
2,5%
α = 0,05
obor
zamítnutí H0
(kritický obor H0)
obor
zamítnutí H0 (kritický
obor H0)obor přijetí H0
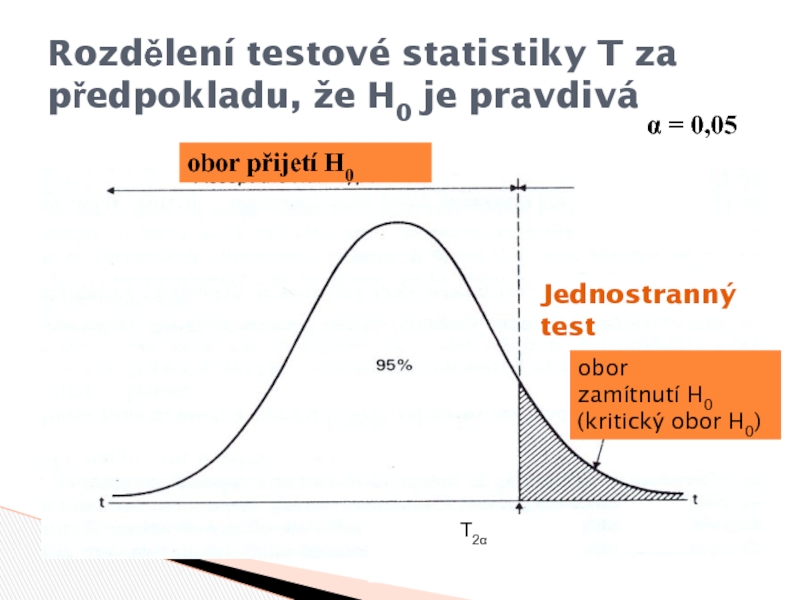
Слайд 8Rozdělení testové statistiky T za předpokladu, že H0 je pravdivá
Jednostranný
test
T2α
obor
zamítnutí H0 (kritický obor H0)
obor
přijetí H0α = 0,05
Слайд 9Rozhodovací pravidlo
(oboustranný test)
Tα… kritická hodnota pro hladinu významnosti α
zamítneme H0
na hladině významnosti α ve prospěch H1
H0 nelze na
hladině významnosti α zamítnoutСлайд 10Alternativní způsob
(při využití statistického SW)
rozhodnutí založeno na p-hodnotě
pravděpodobnost
hodnoty T za předpokladu, že H0 platí
p
na αp>α → nezamítneme H0 na α
Слайд 11chyba 1. druhu
chyba 2. druhu
zamítnutí správné nulové hypotézy
přijetí nesprávné nulové
hypotézy
ppst chyby 1. druhu - hladina významnosti α
ppst chyby
2. druhu - βsíla testu (1- β ) – ppst zamítnutí nesprávné nulové hypotézy
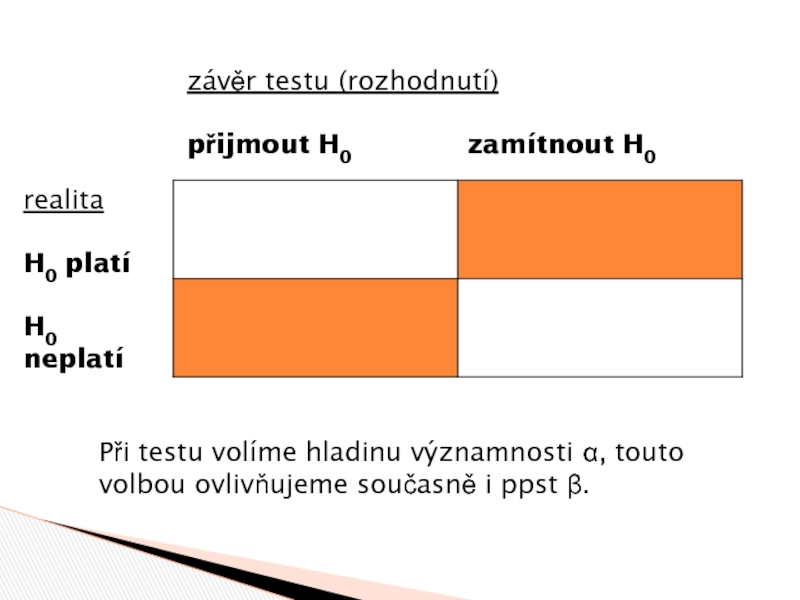
Слайд 12realita
H0 platí
H0 neplatí
závěr testu (rozhodnutí)
přijmout H0 zamítnout H0
Při testu volíme hladinu
významnosti α, touto volbou ovlivňujeme současně i ppst β.
Слайд 13Postup při statistickém testu
1) Formulace nulové a alternativní hypotézy H0
a H1
2) Volba hladiny významnosti α
3) Volba vhodné testové statistiky
T4) Výpočet testového kriteria T na základě výběrových dat
5) Vymezení kritického oboru K pro platnost nulové hypotézy H0 (resp. výpočet p-hodnoty)
6) Rozhodnutí: T leží v kritickém oboru K (resp. p < α ) → zamítnutí H0 T neleží v K (resp. p > α ) → H0 se nezamítá
7) Interpretace statistického rozhodnutí