Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Волны де-Бройля
Содержание
- 1. Волны де-Бройля
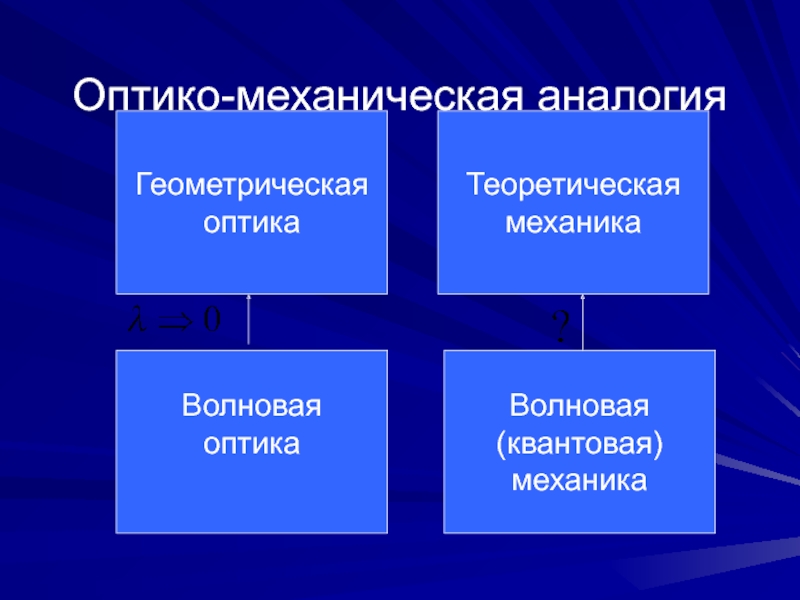
- 2. Оптико-механическая аналогияГеометрическаяоптикаВолноваяоптикаТеоретическаямеханикаВолновая(квантовая)механика
- 3. Оптико-механическая аналогияМежду этими двумя принципами имеется аналогия,
- 4. Гипотеза де-БройляДе-Бройль (de Broglie L.) предположил, что
- 5. Далее, движение материальной частицы характери-зуется четырехмерным вектором
- 6. Волны де-БройляИтак, согласно гипотезе де-Бройля (1924г), микро-частицы
- 7. ФАЗОВАЯ СКОРОСТЬПлоская монохроматическая волна с амплитудой А,
- 8. Продифференцируем (4.5) по времени:откуда
- 9. Суперпозиция волнРассмотренная выше плоская монохроматическая волна представляет
- 10. Образование волновой группыРассмотрим суперпозицию двух волн:распространяющихся вдоль
- 11. Тогда
- 12. ГРУППОВАЯ СКОРОСТЬСкорость перемещения волновой группы - это
- 13. ГРУППОВАЯ СКОРОСТЬ ВОЛН ДЕ-БРОЙЛЯДля волн де-Бройля:(4.11) Таким
- 14. СООТНОШЕНИЕ МЕЖДУ ФАЗОВОЙ И ГРУППОВОЙСКОРОСТЬЮ ВОЛН ДЕ-БРОЙЛЯВернемся
- 15. Гипотеза де-Бройля и правило квантования БораПользуясь понятием
- 16. На круговой орбите стоячая волна возникает, если
- 17. Интернет-экзаменДлина волны де Бройля частицы уменьши-лась вдвое.
- 18. Интернет-экзамен
- 19. Интернет-экзамен
- 20. Интернет-экзамен
- 21. Скачать презентанцию
Оптико-механическая аналогияГеометрическаяоптикаВолноваяоптикаТеоретическаямеханикаВолновая(квантовая)механика
Слайды и текст этой презентации
Слайд 1Физика атома, атомного ядра и элементарных частиц
4. (0). Волновые свойства
микрочастиц. Волны де-Бройля.
Слайд 2Оптико-механическая аналогия
Геометрическая
оптика
Волновая
оптика
Теоретическая
механика
Волновая
(квантовая)
механика
Слайд 3Оптико-механическая аналогия
Между этими двумя принципами имеется аналогия, если предположить, что
где
v - фазовая скорость волны, которую далее бу-дем обозначать vф.
Геометрическая
оптика
Принцип
наименьшеговремени Ферма
(Fermat P.)
Теоретическая
механика
Принцип наименьшего
действия Мопертюи (Maupertuis P.)
Слайд 4Гипотеза де-Бройля
Де-Бройль (de Broglie L.) предположил, что коэффи-циент пропорциональности в
формуле, связываю-щей импульс и фазовую скорость, такой же, как и
для фотона, т.е. равен hν :или
где ν - линейная частота.
Это же соотношение можно записать в виде
(4.1)
где - волновое число, равное числу длин
волн, укладывающихся на отрезок 2π.
Слайд 5Далее, движение материальной частицы характери-зуется четырехмерным вектором энергии-импуль-са {iE/c, px,
py, pz}, а плоская волна - совокупнос-тью четырех величин {iω/c,
kx, ky, kz}, которые также образуют четырехвектор. Поэтому коэффи-циент пропорциональности между энергией и час-тотой, согласно гипотезе де-Бройля, также дол-жен быть таким же, как в оптике:(4.2)
где ω - циклическая частота, связанная с линейной частотой соотношением ω = 2πν.
Формулы (4.1) и (4.2) иногда называют уравнениями де Бройля.
Слайд 6Волны де-Бройля
Итак, согласно гипотезе де-Бройля (1924г), микро-частицы обладают волновыми свойствами.
Длина волны микрочастицы (электрона, протона, нейтро-на, альфа-частицы и др.) называется
дебройлевской длиной волны и определяется формулой де Бройля:(4.3)
где h – постоянная Планка, р = mv – импульс части-цы, v - скорость частицы (не фазовая скорость).
Слайд 7ФАЗОВАЯ СКОРОСТЬ
Плоская монохроматическая волна с амплитудой А, частотой ω и
волновым вектором k может быть представлена в комплексной форме в
виде:(4.4)
Фазовой скоростью волны называется скорость, с которой движутся точки волны с постоянной фа-зой. Если ось x направлена по вектору p, то усло-вие постоянства фазы
Et - px = const. (4.5)
Чтобы вычислить фазовую скорость, надо продиф-ференцировать это уравнение по времени.
Слайд 8
Продифференцируем (4.5) по времени:
откуда
, где
- фазовая скорость.По формулам (4.1) и (4.2) находим:
С другой стороны:
где v - скорость частицы.
Итак, фазовая скорость: (4.6)
Слайд 9Суперпозиция волн
Рассмотренная выше плоская монохроматическая волна представляет строго периодический про-цесс,
бесконечно протяженный в пространстве и во времени. Это абстракция; в
природе такие волны не существуют. Любой реальный процесс имеет начало и конец, он ограничен как во вре-мени, так и в пространстве и не является строго гармоническим. Его можно рассматривать как ре-зультат суперпозиции (наложения) гармоничес-ких волн, которые вследствие интерференции в одних частях пространства усиливают друг дру-га, а в других - гасят друг друга.Слайд 10Образование волновой группы
Рассмотрим суперпозицию двух волн:
распространяющихся вдоль оси x. Будем
считать, что частоты ω1 и ω2, а также абсолютные значе-ния
волнового вектора k1 и k2 очень мало отлича-ются друг от друга. Складывая u1 и u2, находим:Обозначим:
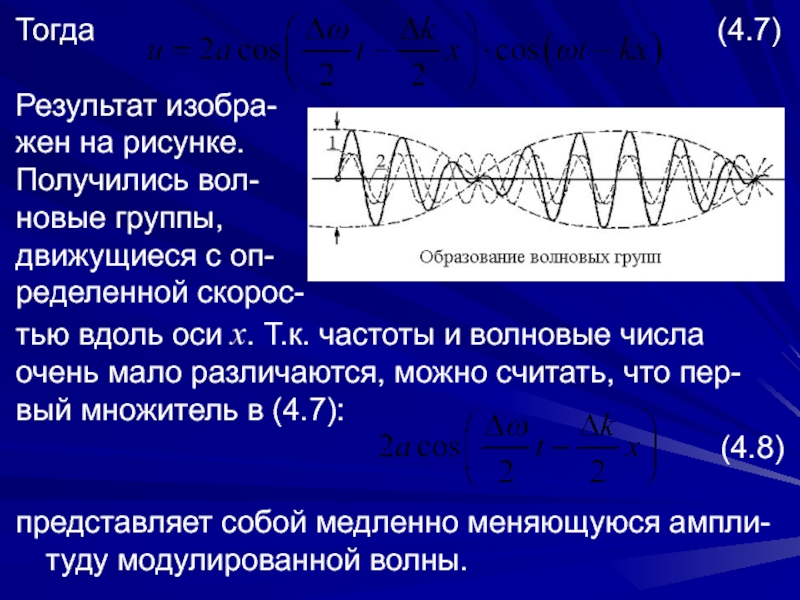
Слайд 11Тогда
(4.7)
Результат изобра-
жен на рисунке.
Получились вол-
новые группы,
движущиеся с оп-
ределенной скорос-
тью вдоль оси x. Т.к. частоты и волновые числа
очень мало различаются, можно считать, что пер-
вый множитель в (4.7):
(4.8)
представляет собой медленно меняющуюся ампли-туду модулированной волны.
Слайд 12ГРУППОВАЯ СКОРОСТЬ
Скорость перемещения волновой группы - это ско-рость перемещения определенной
амплитуды. Для ее определения запишем условие постоянст-ва амплитуды:
(4.9)
Дифференцируя (4.9) по
t, получаем скорость пере-мещения волновой группы:В пределе получаем формулу для групповой скорости:
(4.10)
Слайд 13ГРУППОВАЯ СКОРОСТЬ ВОЛН ДЕ-БРОЙЛЯ
Для волн де-Бройля:
(4.11)
Таким образом, скорость частицы
v равна групповой скорости волн де-Бройля vгр
Слайд 14СООТНОШЕНИЕ МЕЖДУ ФАЗОВОЙ И ГРУППОВОЙ
СКОРОСТЬЮ ВОЛН ДЕ-БРОЙЛЯ
Вернемся к формуле (4.6)
и запишем ее в виде
или (4.12)Из этой формулы следует, что фазовая скорость волн де-Бройля всегда больше скорости света (т.к. скорость частицы v всегда меньше скорости све-та). Это, однако, не противоречит теории относи-тельности, т.к. фазовая скорость не характеризует ни скорость перемещения массы, ни скорость пе-ремещения энергии.
Слайд 15Гипотеза де-Бройля
и правило квантования Бора
Пользуясь понятием дебройлевской длины волны, можно
дать наглядное истолкова-ние правилу квантования круговых орбит. Электрон обладает волновыми
свойства-ми. Чтобы энергия волнового движения не распространялась в другие области (т.е. чтобы электрон при движении вокруг ядра не излучал энергию), волна должна быть стоячей.Слайд 16На круговой орбите стоячая волна возникает, если на этой орбите
уложится целое число длин волн де-Бройля: 2πr= nλ. Отсюда, учитывая,
что λ = h/mv, находим:т.е. правило квантования.
Таким образом, 1-ый постулат Бора – логическое следствие волновой природы электрона.
Слайд 17Интернет-экзамен
Длина волны де Бройля частицы уменьши-лась вдвое. Скорость этой частицы
…
ВАРИАНТЫ ОТВЕТОВ:
1) не изменилась
2) уменьшилась в 4 раза
3) увеличилась
в 4 раза4) уменьшилась вдвое
5) увеличилась вдвое