Слайд 14.1 Второе начало термодинамики
ЛЕКЦИЯ 4. ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
Слайд 2Формулировки второго начала термодинамики
Второе начало термодинамики определяет условия, при которых
возможны превращения энергии, описывающиеся уравнением первого начала термодинамики, а также
направления протекания этих процессов.
1-я формулировка (по Клаузиусу): невозможен самопроизвольный переход тепла от менее к более нагретому телу, т.е. невозможны процессы, единственным конечным результатом которых был бы переход тепла от менее к более нагретому телу.
2-я формулировка (по Кельвину): невозможны процессы, единственным конечным результатом которых было бы превращение тела целиком в работу.
Слайд 3Другой вид формулировки второго начала термодинамики по Кельвину
Вечный двигатель второго
рода невозможен, т.е. невозможно создать тепловой двигатель с КПД, равным
1.
КПД любого двигателя равен отношению работы A, произведенной рабочим веществом за цикл, к сообщенному рабочему веществу теплу Q1:
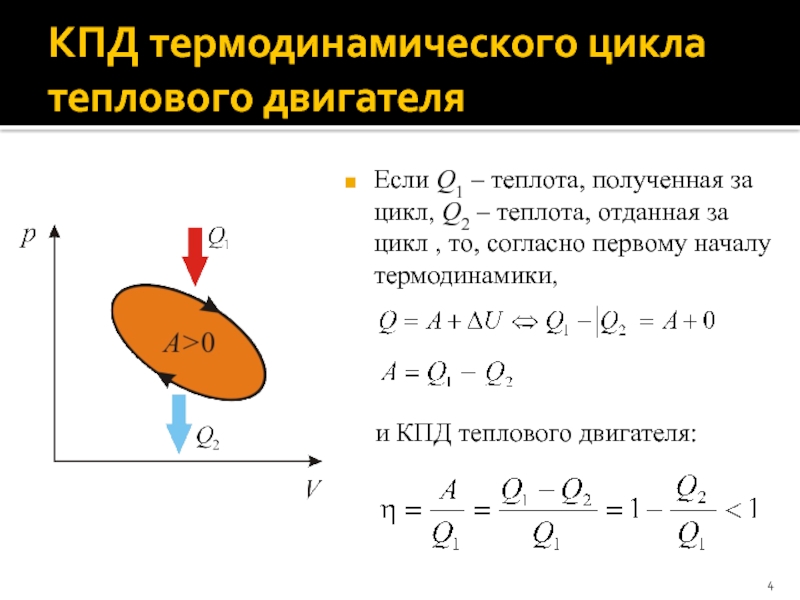
Слайд 4КПД термодинамического цикла теплового двигателя
Если Q1 – теплота, полученная за
цикл, Q2 – теплота, отданная за цикл , то, согласно
первому началу термодинамики,
и КПД теплового двигателя:
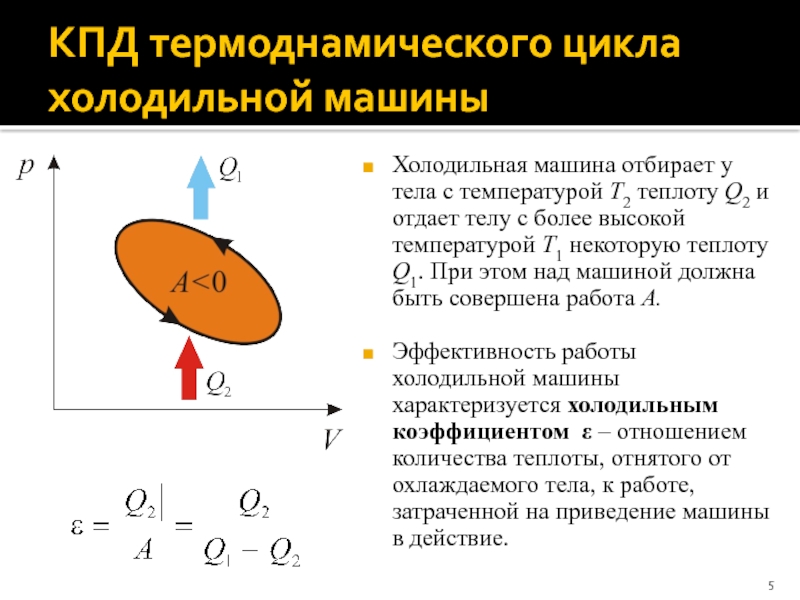
Слайд 5КПД термоднамического цикла холодильной машины
Холодильная машина отбирает у тела с
температурой T2 теплоту Q2 и отдает телу с более высокой
температурой T1 некоторую теплоту Q1. При этом над машиной должна быть совершена работа A.
Эффективность работы холодильной машины характеризуется холодильным коэффициентом ε – отношением количества теплоты, отнятого от охлаждаемого тела, к работе, затраченной на приведение машины в действие.
Слайд 64.2 Обратимые и необратимые процессы. Энтропия системы
ЛЕКЦИЯ 4. ВТОРОЕ И
ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
Слайд 7Обратимость процессов в механике
Простые механические движения всегда обратимы. Например:
колебания математического
маятника;
упругое соударение тел.
Обратимость процесса, в широком смысле, означает, что при
его реализации в окружающей среде ничего не изменяется.
Слайд 8Пример необратимого процесса: движение пули в воздухе
Слайд 9Вопрос об обратимости процессов в термодинамике
Нельзя ли с помощью каких-либо
процессов или механизмов добиться того, чтобы участвующих в них тела
вернулись в исходное состояние без того, чтобы в окружающей среде произошли какие-либо изменения?
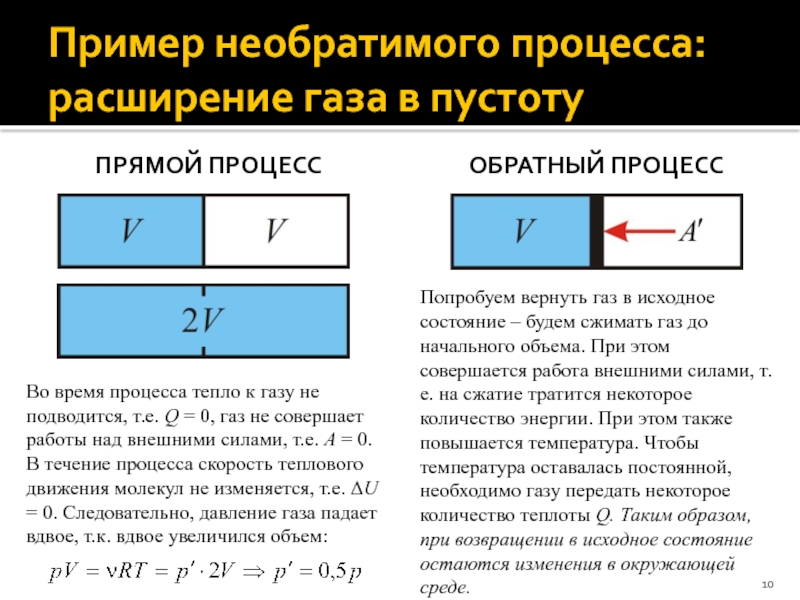
Слайд 10Пример необратимого процесса: расширение газа в пустоту
ПРЯМОЙ ПРОЦЕСС
ОБРАТНЫЙ ПРОЦЕСС
Во время
процесса тепло к газу не подводится, т.е. Q = 0,
газ не совершает работы над внешними силами, т.е. A = 0. В течение процесса скорость теплового движения молекул не изменяется, т.е. ΔU = 0. Следовательно, давление газа падает вдвое, т.к. вдвое увеличился объем:
Попробуем вернуть газ в исходное состояние – будем сжимать газ до начального объема. При этом совершается работа внешними силами, т.е. на сжатие тратится некоторое количество энергии. При этом также повышается температура. Чтобы температура оставалась постоянной, необходимо газу передать некоторое количество теплоты Q. Таким образом, при возвращении в исходное состояние остаются изменения в окружающей среде.
Слайд 11Пример обратимого термодинамического процесса: адиабатический процесс
При адиабатическом процессе нет теплообмена
с окружающей средой, т.е. Q = 0, и внешняя механическая
работа совершается только за счет внутренней энергии газа: A = –ΔU.
Если внешние тела совершают над газом работу A = –A′, то эта механическая работа переходит во внутреннюю энергию газа, и газ вернется в исходное состояние без каких-либо изменений в окружающих телах.
Слайд 12Пример обратимого термодинамического процесса: изотермическое сжатие
При изотермическом сжатии температура газа
остается постоянной, равной температуре окружающей среды. Следовательно, ΔU = 0,
и внешняя работа совершается за счет внешнего тела: Q = A. Вся система находится в тепловом равновесии. Т.е. этот бесконечно медленный процесс превращается в бесконечную последовательность равновесных состояний.
Слайд 13Квазистатические процессы
Квазистатический процесс – это процесс, текущий бесконечно медленно и
представляющий собой бесконечную последовательность равновесных состояний.
При этом для любых двух
состояний такого процесса может быть любой порядок: процесс может остановиться и пойти вспять, затем снова остановиться и пойти в прежнем направлении.
Таким образом, все квазистатические процессы обратимы.
Однако многочисленные опытные данные показывают, что реальные тепловые процессы всегда необратимы (реальные, т.к. и адиабатический, и изотермический процессы, в принципе, не реальны).
Слайд 14Энтропия
В термодинамике энтропия вводится через элементарное приращение:
и является полным дифференциалом,
т.е. функцией состояния системы и не зависит от вида процесса.
В этом случае изменение энтропии определяется лишь начальным и конечным состояниями системы:
где состояния 1 и 2 должны быть равновесными, а процесс 1-2 может быть любым, даже необратимым.
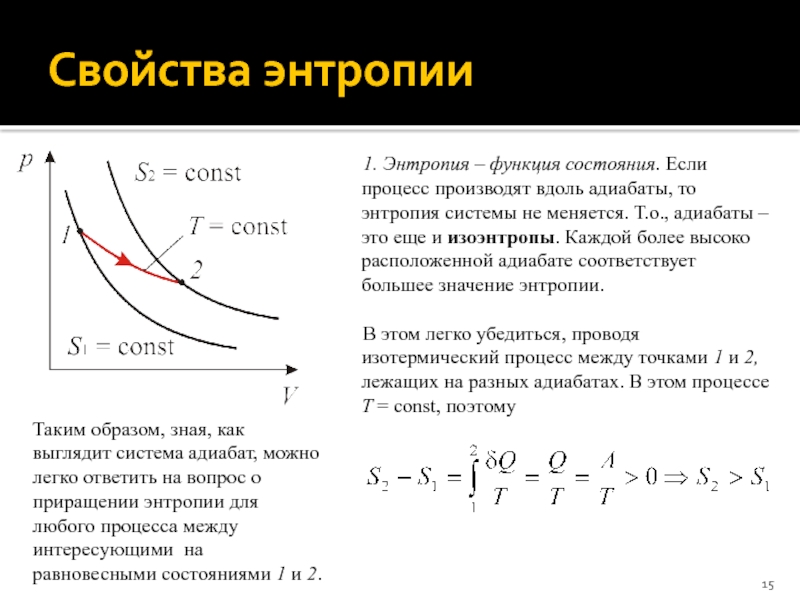
Слайд 15Свойства энтропии
1. Энтропия – функция состояния. Если процесс производят вдоль
адиабаты, то энтропия системы не меняется. Т.о., адиабаты – это
еще и изоэнтропы. Каждой более высоко расположенной адиабате соответствует большее значение энтропии.
В этом легко убедиться, проводя изотермический процесс между точками 1 и 2, лежащих на разных адиабатах. В этом процессе T = const, поэтому
Таким образом, зная, как выглядит система адиабат, можно легко ответить на вопрос о приращении энтропии для любого процесса между интересующими на равновесными состояниями 1 и 2.
Слайд 16Свойства энтропии
2. Энтропия – величина аддитивная: энтропия макросистемы равна сумме
энтропий ее частей.
3. Принцип возрастания энтропии: энтропия замкнутой (теплоизолированной )
макросистемы не уменьшается – она либо возрастает (для необратимых процессов), либо остается постоянной (для обратимых процессов).
Таким образом, величина изменения (возрастания) энтропии замкнутой ΔS системы может служить мерой необратимости процессов, протекающих в этой системе. В предельном случае, если процессы имеют обратимый характер, то энтропия замкнутой системы не изменяется, т.е. ΔS = 0.
Слайд 17Изменение энтропии и процессы в природе
Все самопроизвольно протекающие процессы в
природе – от теплообмена до химических реакций – протекают таким
образом, что энтропия возрастает. Необходимо специальное взаимодействие с окружающей средой, чтобы препятствовать возрастанию энтропии в системе. Наиболее ярким примером могут служить живые существа.
Слайд 18Теорема Нернста
Эта теорема утверждает, что при приближении температуры к абсолютному
нулю энтропия системы также стремится к нулю:
При этом теплоемкость системы
также стремится к нулю.
Теорему Нернста называют третьим началом термодинамики.
Слайд 194.3 Вычисление энтропии. Основное уравнение термодинамики
ЛЕКЦИЯ 4. ВТОРОЕ И ТРЕТЬЕ
НАЧАЛА ТЕРМОДИНАМИКИ
Слайд 20Основное уравнение термодинамики
Оно представляет собой объединение первого начала термодинамики и
выражения для элементарного приращения энтропии. Если учесть, что
то уравнение первого
начала термодинамики примет вид:
Слайд 21Энтропия идеального газа
Пусть начальное 1 и конечное 2 состояния идеального
газа характеризуются параметрами p1, V1 и p2, V2. Тогда элементарное
приращение энтропии
Возьмем дифференциал логарифма от уравнения состояния идеального газа:
Слайд 22Энтропия идеального газа
Подставим это выражение в уравнение для элементарного приращения
энтропии:
Интегрируя обе части данного выражения, получим:
Слайд 23Приращение энтропии в необратимом процессе
Непосредственно считать изменение энтропии в каком-либо
необратимом процессе невозможно. Однако, энтропия – функция состояния. Эти свойством
можно воспользоваться, проведя между начальным и конечным состояниями какой-нибудь обратимый процесс, ничего общего не имеющий с реальным необратимым процессом.
ПРИМЕР. Пусть в одном из теплоизолированных сосудов равного объема V, находится один моль идеального газа, а в другом – вакуум. Вентиль открыли, газ заполнил оба сосуда (необратимый процесс) и пришел в состояние термодинамического равновесия. Найдем приращение энтропии в процессе.
Процесс шел без теплообмена: Q = 0 и без совершения работы: A = 0. Значит, по первому началу термодинамики, ΔU = 0 и конечная температуры равна первоначальной. Это позволяет произвести расчет изменения энтропии по обратимому изотермическому процессу
Слайд 24Возрастание энтропии при смешении газов
После необратимого процесса смешения газов система
перейдем в равновесное состояние, при котором газы перемешаны. Как в
предыдущем примере, для каждого из газов:
Тогда суммарное приращение энтропии системы
Энтропия системы увеличивается, т.е. процесс необратим (саморазделение газов на составляющие – процесс невероятный).
Пусть в 2-х половинах теплоизолированного сосуда находятся два идеальных газа, разделенные перегородкой. Количество молей и давления газов одинаковы. Найдем изменение энтропии при удалении перегородки
Слайд 25Парадокс Гиббса
Последняя формулы приводит к выводу, называемому парадоксом Гиббса:
Допустим,
что газы 1 и 2 тождественны. Тогда после удаления перегородки
энтропия увеличивается, хотя ясно, что состояние системы ничем не отличается от первоначального.
Для понимания описанной ситуации существенно знать, что последняя формула получена только для случая, когда газы 1 и 2 различны. Для тождественных газом приведенные рассуждения неприменимы, для них ΔS = 0.
Слайд 264.4 Цикл Карно
ЛЕКЦИЯ 4. ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
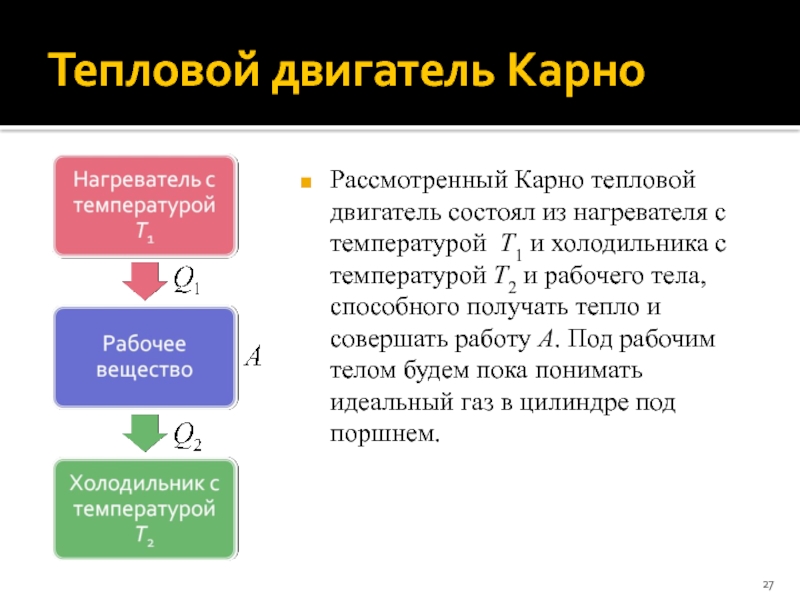
Слайд 27Тепловой двигатель Карно
Рассмотренный Карно тепловой двигатель состоял из нагревателя с
температурой T1 и холодильника с температурой T2 и рабочего тела,
способного получать тепло и совершать работу A. Под рабочим телом будем пока понимать идеальный газ в цилиндре под поршнем.
Слайд 28Цикл Карно
Карно рассмотрел цикл, состоящий из двух изотерм и двух
адиабат. При изотермическом расширении 1-2 газ находится в контакте с
нагревателем (T1). При этом газ получает тепло Q1. На изотерме 3-4 газ отдает тепло Q2 холодильнику (T2).
Данный цикл является обратимым (если его проводить бесконечно медленно). Он также может быть проведен в обратном направлении, при этом газ совершает отрицательную работу, нагреватель получает тепло Q1, холодильник отдает газу тепло Q2, которое он получил в прямом цикле. Именно так работает холодильная машина.
Слайд 29Вывод формулы для КПД цикла Карно
На диаграмме TS цикл Карно
имеет вид прямоугольника с изотермами 1-2 и 3-4 (горизонтальные прямые)
и адиабатами (изоэнтропами) 2-3 и 4-1 (вертикальные прямые). Полученное тепло
и равно площади под отрезком 1-2. Отданное тепло
и равно площади под отрезком 3-4. Тогда работа газа за цикл:
Слайд 30КПД цикла Карно
Тогда КПД цикла Карно:
При выводе этой формулы не
делалось никаких выводов о свойствах рабочего вещества и устройстве теплового
двигателя. Отсюда следует теорема Карно:
КПД обратимых двигателей, работающих по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства двигателя, ни от рода рабочего вещества.
Слайд 312-я теорема Карно
КПД любого необратимого теплового двигателя, работающего с теми
же температурами нагревателя и холодильника, всегда меньше, чем у двигателя,
работающего по обратимому циклу Карно:
Слайд 32Другие процессы на диаграмме TS
Решение вопроса о КПД других циклов
часто сильно упрощается, если его рассматривать в переменных TS. Во
многих циклах встречаются участки – изохоры и изобары. Выясним, как они выглядят на диаграмме TS.
Пусть начальное состояние идеального газа определяется параметрами p0 и V0. Элементарное приращение энтропии газа:
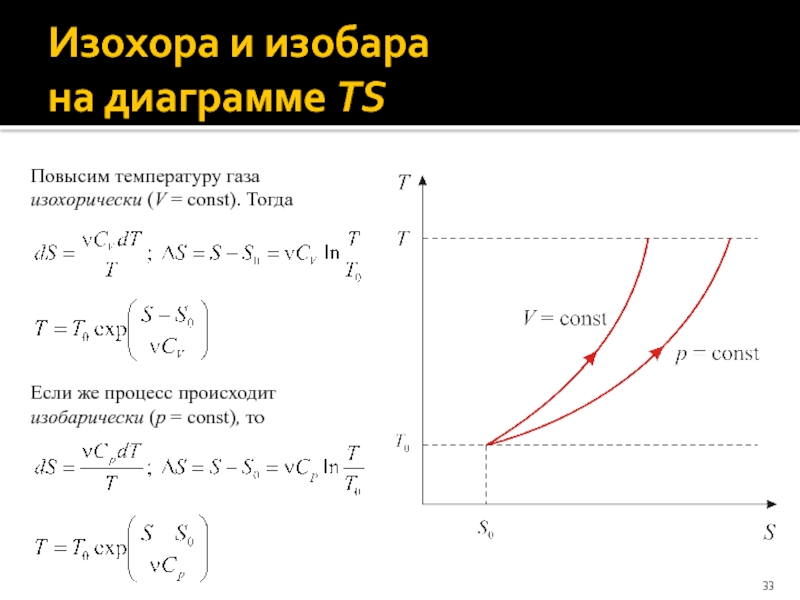
Слайд 33Изохора и изобара
на диаграмме TS
Повысим температуру газа
изохорически (V =
const). Тогда
Если же процесс происходит
изобарически (p = const), то
Слайд 344.5 Энтропия и вероятность. Статистический смысл энтропии
ЛЕКЦИЯ 4. ВТОРОЕ И
ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
Слайд 35Макро- и микросостояния системы. Статистический вес
Состояние макросистемы, охарактеризованное заданием таких
макропараметром, как объем, температура, давление и др., называется макросостоянием.
Состояние макросистемы,
при котором заданы состояния всех молекул, входящих в систему, называют микросостоянием.
Любое макросостояние может быть выражено различными способами, т.е. различными микросостояниями. Число микросостояний, с помощью которых может быть реализовано данное макросостояние системы, называется статистическим весом макросостояния.
Слайд 36Размещение N молекул по двум половинкам сосуда
Вероятность одновременного пребывания N
молекул в одной и половинок сосуда равна 1/2N.
Таким образом,
вероятность любого размещения четырех молекул также равна 1/2N.
Каждое размещение – это некоторое микросостояние системы, и вероятность P каждого размещения одинакова и равна 1/2N.
Рассмотрим способы, с помощью которых молекул могут быть распределены между двумя половинками сосуда с газом. Рассмотрим случай, когда в сосуде, мысленно разделенным на две одинаковые половины A и B, находятся N = 4 молекулы.
Перенумеруем их: 1, 2, 3, 4.
Каждая молекула с вероятностью ½ может находиться в одной из половинок сосуда.
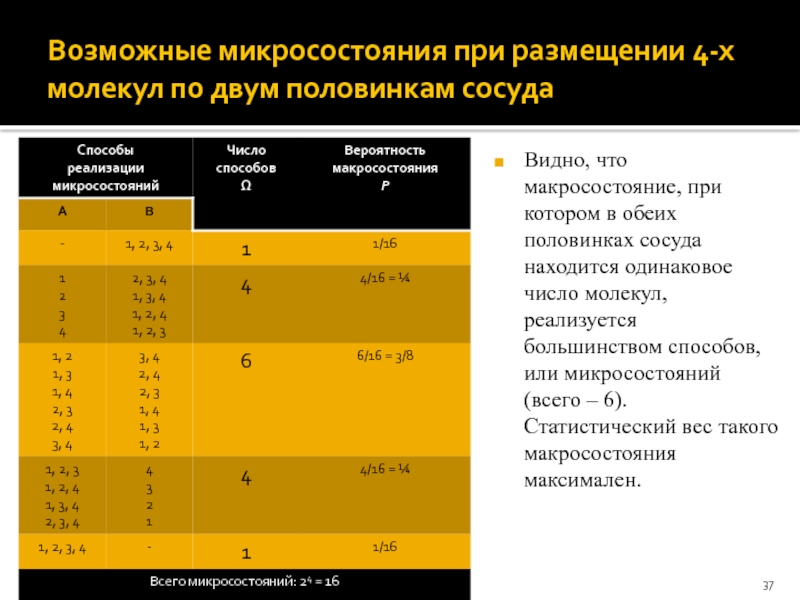
Слайд 37Возможные микросостояния при размещении 4-х молекул по двум половинкам сосуда
Видно,
что макросостояние, при котором в обеих половинках сосуда находится одинаковое
число молекул, реализуется большинством способов, или микросостояний (всего – 6). Статистический вес такого макросостояния максимален.
Слайд 38Самопроизвольное сжатие газа
Пусть первоначально все 4 молекул идеального газа находились
в половине A. Вследствие беспорядочного движения молекул некоторые из молекул
окажутся в половине B сосуда, т.е. газ расширяется. Может оказаться так, что в какой-то момент времени все 4 молекулы снова окажутся в одной из половинок сосуда: газ самопроизвольно сжимается, т.е. процесс оказывается обратимым.
Поскольку скорость молекул достаточно велика, процесс самопроизвольного сжатия газа наступит очень скоро.
Слайд 39Случай распределения большого числа молекул по двум половинам сосуда
В случае
N = 10 получим P ~ 10-3. Таким образом, если
в течение длительного времени фиксировать распределение молекул по половинкам сосуда через равные промежутки времени, то окажется, что в одном из 1000 случаев в среднем окажется, что все 10 молекул окажутся в одной половине сосуда.
Если N = 100, мы получим P ~ 10-30.
Если N = 1020, то окажется, что P ~ 10-3⋅10-19. Такова вероятность, что газ самопроизвольно сожмется в одной половине сосуда. Ясно, что такое событие практически неосуществимо.
При N → ∞ статистический вес макросостояния, при котором в обеих половинках сосуда содержится одинаковое число молекул стремительно растет:
Слайд 40Вывод
Макросистема, будучи предоставленной самой себе, стремится самопроизвольно переходить от менее
вероятных макросостояний, к более вероятным.
В этом состоит суть необратимости
процесса.
Таким образом, обратный процесс возможен, но вероятность его реализации пренебрежимо мала.
Слайд 41Энтропия и вероятность.
Формула Больцмана
Если макросистема находится в неравновесном состоянии,
то она будет самопроизвольно переходить в состояние с большей вероятностью
– в равновесное состояние. Вместе с тем, согласно второму началу термодинамики, все самопроизвольные процессы в замкнутых системах сопровождаются возрастанием энтропии. Поэтому между энтропией состояния и вероятностью этого состояния существует связь:
где k – постоянная Больцмана, Ω – статистический вес макросостояния с энтропией S.
Слайд 42Вывод Больцмана
Все замкнутые макросистемы стремятся переходить от состояний менее вероятных
к более вероятным.
При этом энтропия характеризует степень беспорядка в системе:
состояниям с большим беспорядком соответствует большая в вероятность (или статистический вес Ω), чем у более упорядоченного состояния.
С этим связана необратимость реальных тепловых процессов: они протекают так, что беспорядок в системе увеличивается. С этим связан тот факт, что любой вид энергии в конце концов переходит во внутреннюю энергию, т.е. в состояние, при котором «хаос» в системе максимален. Это состояние является равновесным и его энтропия S = max.