Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обратная функция
Содержание
- 1. Обратная функция
- 2. Обратная функцияТема:
- 3. Цели обучения:10.3.1.5 - знать определение обратной функции
- 4. Критерии оценивания:Учащийся Знает определение обратной функции; Знает
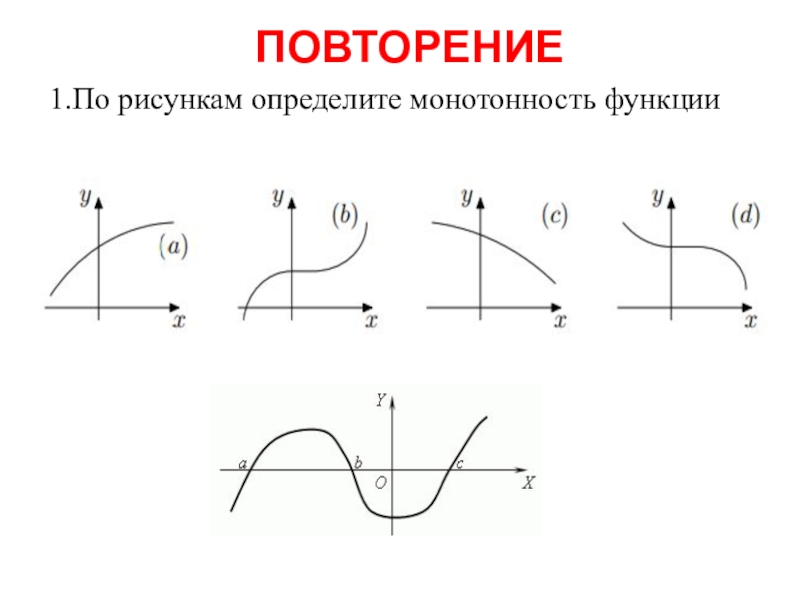
- 5. ПОВТОРЕНИЕ1.По рисункам определите монотонность функции
- 6. Если функция у = f ( х
- 7. Теорема. Если функция у=f(x) строго монотонна на
- 8. Функция у = f(x) обратима на некотором
- 9. ПримерДано:Найти функцию, обратную данной, т.е. у =
- 10. ВТОРОЙ СПОСОБАлгоритм нахождения обратной функции:Выражаем х на
- 11. ПримерДано:Найти функцию, обратную данной, т.е. у =
- 12. Слайд 12
- 13. Свойства взаимно обратных функций.1) Область определения. Пусть f
- 14.
- 15. Скачать презентанцию
Обратная функцияТема:
Слайды и текст этой презентации
Слайд 4Критерии оценивания:
Учащийся
Знает определение обратной функции;
Знает особенность расположения
графиков взаимно обратных функций;
Находит функцию, обратную заданной.
Слайд 6Если функция у = f ( х ), х €
Х принимает каждое своё значение у только при одном значении
х из Х, то эту функцию называют обратимой.Т.е. разным значениям аргумента соответствуют разные значения функции
Слайд 7Теорема. Если функция у=f(x) строго монотонна на множестве Х., то
она обратима
Пусть у = f(x) – обратимая функция. Тогда каждому
у из множества значений функции соответствует одно определённое число х из области её определения, такое, что f(x) = y. Это соответствие определяет функцию х от у, которую обозначим х = g(y). Поменяем местами х и у: у = g(x).
Функцию у = g(x) называют обратной к функции у = f(x).
Слайд 8Функция у = f(x) обратима на некотором интервале (a; b)
тогда и только тогда, когда она на этом интервале взаимно
однозначна.Алгоритм нахождения обратной функции:
Заменяем х на у
Выражаем у
Получаем функцию у = g(x), обратную функции у = f(x).
Примечание: иногда обратную функцию обозначают:
Слайд 10ВТОРОЙ СПОСОБ
Алгоритм нахождения обратной функции:
Выражаем х на у
Меняем местами у
и х
Получаем функцию у = g(x), обратную функции у =
f(x).Слайд 13Свойства взаимно обратных функций.
1) Область определения. Пусть f и g –
взаимно обратные функции. Область определения функции f совпадает с областью
значений функции g, и наоборот, область значений функции f совпадает с областью определения функции g.2) Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное верно и для убывающих функций.
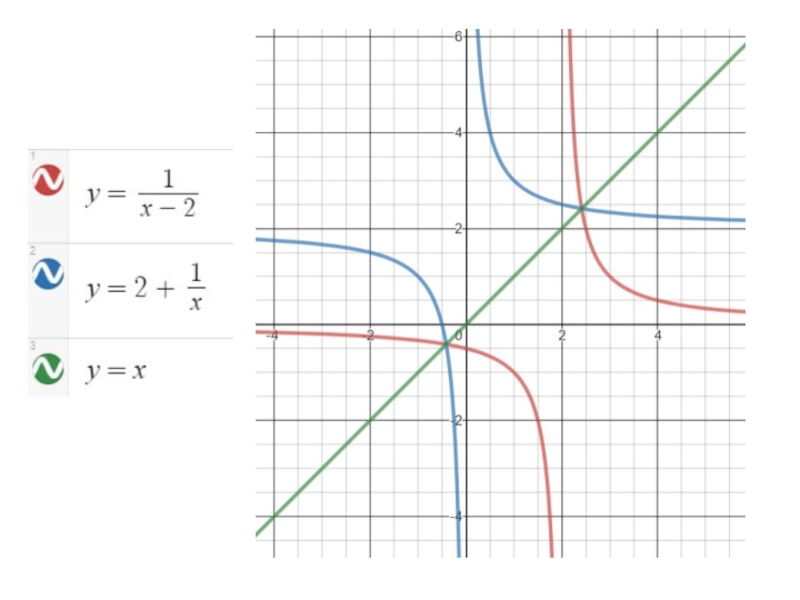
3) Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой y = x.