Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
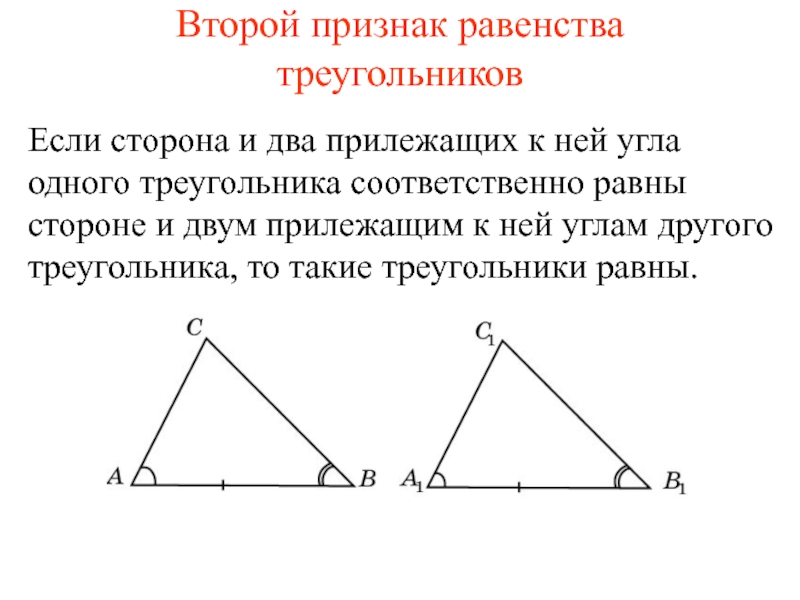
Второй признак равенства треугольников
Содержание
- 1. Второй признак равенства треугольников
- 2. Упражнение 1На рисунке угол 1 равен углу
- 3. Упражнение 2Ответ: а) AB = CD; AD
- 4. Упражнение 3Ответ: а) ABC и ADC; б)
- 5. На рисунке BC = CD, угол B
- 6. В четырехугольнике ABCD угол 1 равен углу
- 7. Упражнение 6На рисунке угол DBC равен углу
- 8. Упражнение 7Доказательство: Треугольники ABC и DEF равны
- 9. Упражнение 8Доказательство: Треугольники AOC и DOB равны
- 10. Упражнение 9Доказательство: Треугольники AOB и COD равны
- 11. Упражнение 10Лучи AD и ВС пересекаются в
- 12. Упражнение 11Лучи AD и ВС пересекаются в
- 13. Упражнение 12Решение: Треугольники ABC и CDA равны
- 14. Упражнение 13На рисунке угол DAB равен углу
- 15. Упражнение 14Решение: Треугольники ABC и BAD равны
- 16. Упражнение 15В четырехугольнике ABCD угол DAB равен
- 17. Упражнение 16Треугольники АВС и А1В1С1 равны. Отрезки
- 18. Упражнение 17На рисунке AE=AC, угол 1 равен
- 19. Упражнение 18На рисунке AE=AC, угол 1 равен
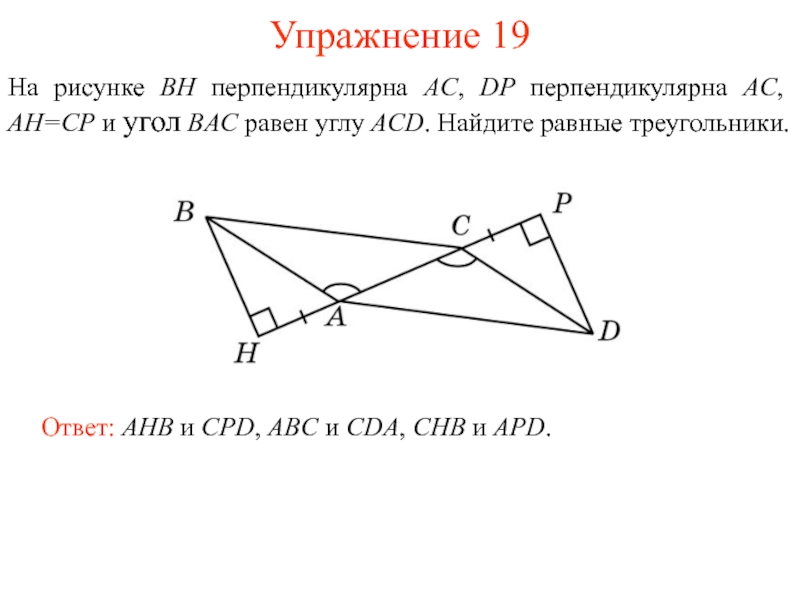
- 20. Упражнение 19Ответ: AHB и CPD, ABC и
- 21. Упражнение 20По рисунку объясните, как можно найти
- 22. Скачать презентанцию
Упражнение 1На рисунке угол 1 равен углу 3, угол 2 равен углу 4. Будут ли треугольники CDA и ABC равны? Ответ: Да. Треугольники CDA и ABC равны по второму признаку равенства
Слайды и текст этой презентации
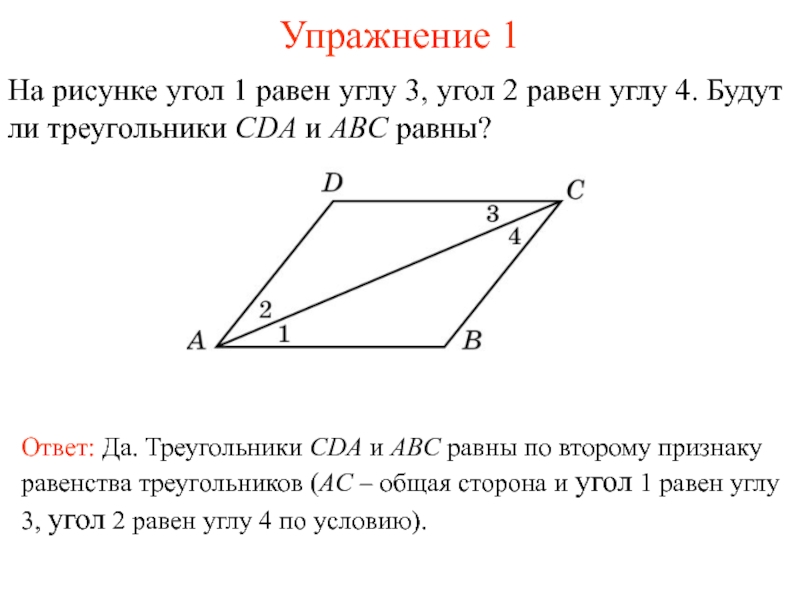
Слайд 2Упражнение 1
На рисунке угол 1 равен углу 3, угол 2
равен углу 4. Будут ли треугольники CDA и ABC равны?
Ответ: Да. Треугольники CDA и ABC равны по второму признаку равенства треугольников (AC – общая сторона и угол 1 равен углу 3, угол 2 равен углу 4 по условию).
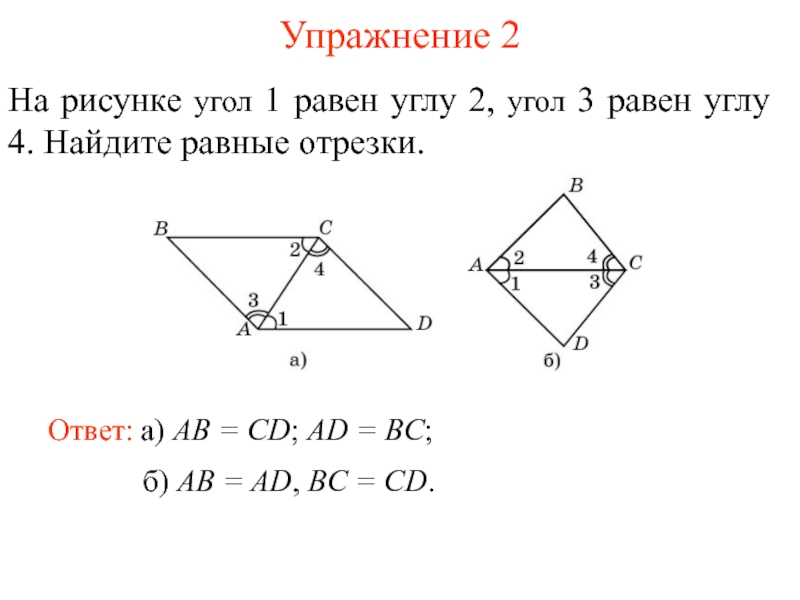
Слайд 3Упражнение 2
Ответ: а) AB = CD; AD = BC;
На
рисунке угол 1 равен углу 2, угол 3 равен углу
4. Найдите равные отрезки.б) AB = AD, BC = CD.
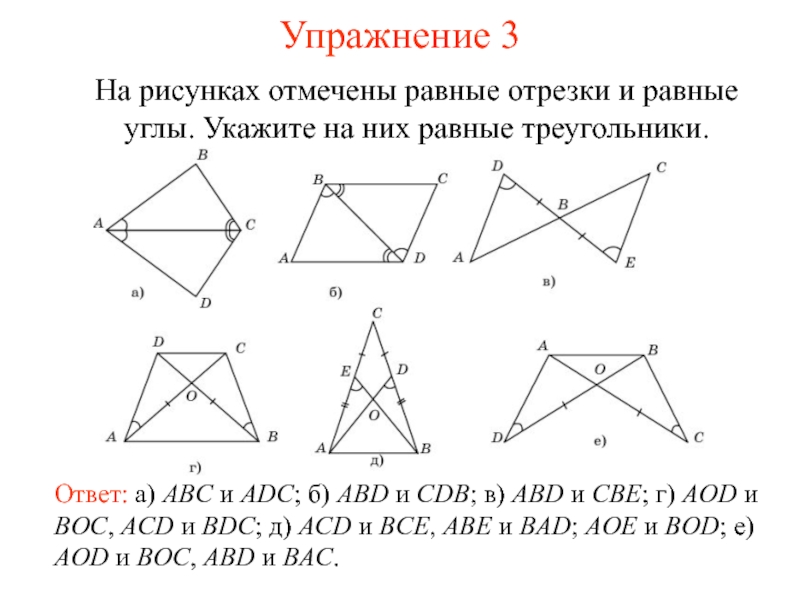
Слайд 4Упражнение 3
Ответ: а) ABC и ADC; б) ABD и CDB;
в) ABD и CBE; г) AOD и BOC, ACD и
BDC; д) ACD и BCE, ABE и BAD; AOE и BOD; е) AOD и BOC, ABD и BAC.На рисунках отмечены равные отрезки и равные углы. Укажите на них равные треугольники.
Слайд 5На рисунке BC = CD, угол B равен углу D.
Докажите, что AC = CE.
Решение. Углы ACB и ECD
равны как вертикальные. Треугольники ABC и EDC равны по второму признаку равенства треугольников (BC = DC, угол ABC равен углу EDC, угол ACB равен углу ECD). Следовательно, равны соответствующие стороны AC и CE этих треугольников. Упражнение 4
Слайд 6В четырехугольнике ABCD угол 1 равен углу 2, угол 3
равен углу 4. Докажите, что АB = AD.
Решение. Треугольники
ABC и ADC равны по второму признаку равенства треугольников (AC – общая сторона, угол 1 равен углу 2, угол 3 равен углу 4. ). Следовательно, равны их соответствующие стороны AB и AD. Упражнение 5
Слайд 7Упражнение 6
На рисунке угол DBC равен углу DAC, BO =
AO. Докажите, что угол C равен углу D и AC
= BD.Доказательство: Треугольники AOC и BOD равны по второму признаку равенства треугольников (AO = BO, угол OAC равен углу OBD, угол AOC равен углу BOD). Следовательно, угол C равен углу D и AC = BD.
Слайд 8Упражнение 7
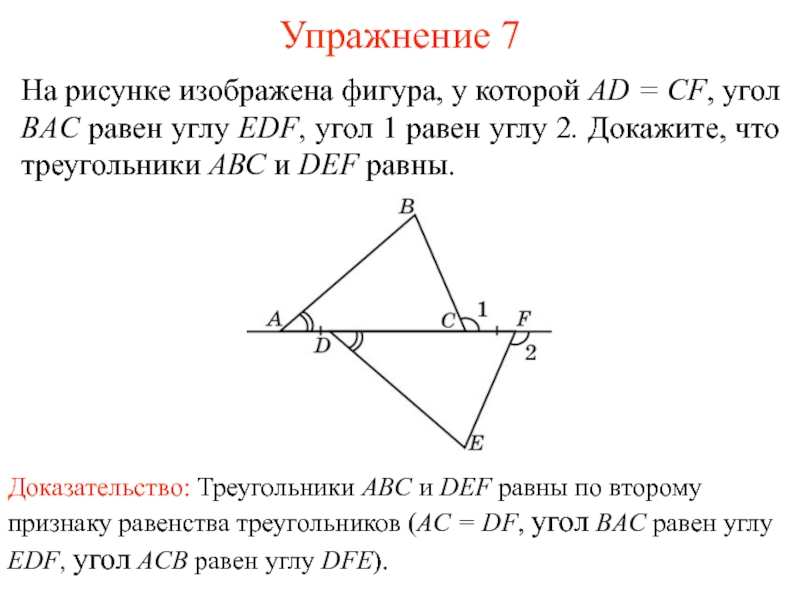
Доказательство: Треугольники ABC и DEF равны по второму признаку
равенства треугольников (AC = DF, угол BAC равен углу EDF,
угол ACB равен углу DFE).На рисунке изображена фигура, у которой AD = CF, угол ВAC равен углу EDF, угол 1 равен углу 2. Докажите, что треугольники АВС и DEF равны.
Слайд 9Упражнение 8
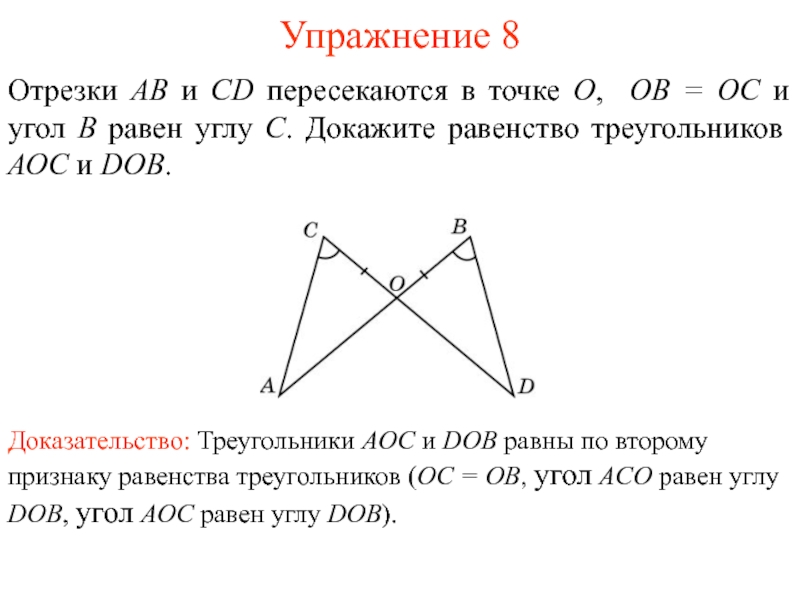
Доказательство: Треугольники AOC и DOB равны по второму признаку
равенства треугольников (OC = OB, угол ACO равен углу DOB,
угол AOC равен углу DOB).Отрезки АВ и CD пересекаются в точке О, ОВ = ОС и угол B равен углу C. Докажите равенство треугольников АОС и DOB.
Слайд 10Упражнение 9
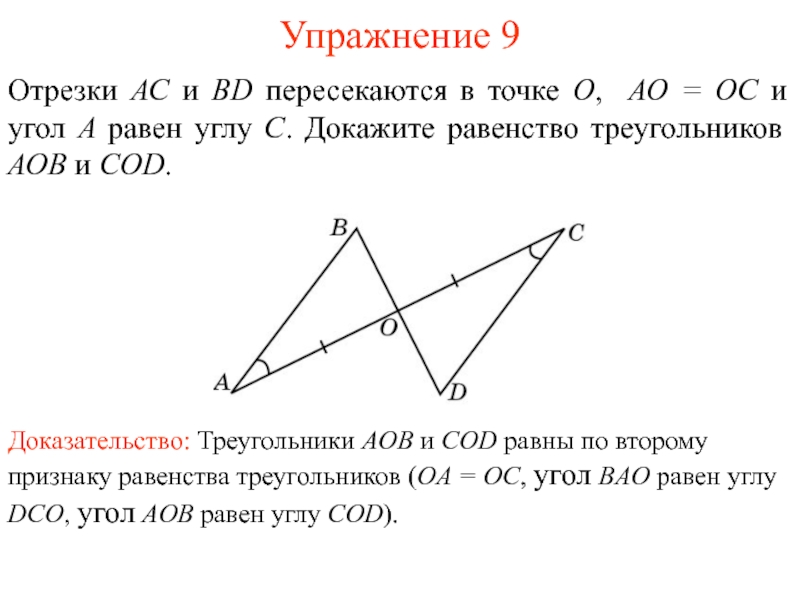
Доказательство: Треугольники AOB и COD равны по второму признаку
равенства треугольников (OA = OC, угол BAO равен углу DCO,
угол AOB равен углу COD).Отрезки АС и BD пересекаются в точке О, АО = ОС и угол A равен углу C. Докажите равенство треугольников АОВ и COD.
Слайд 11Упражнение 10
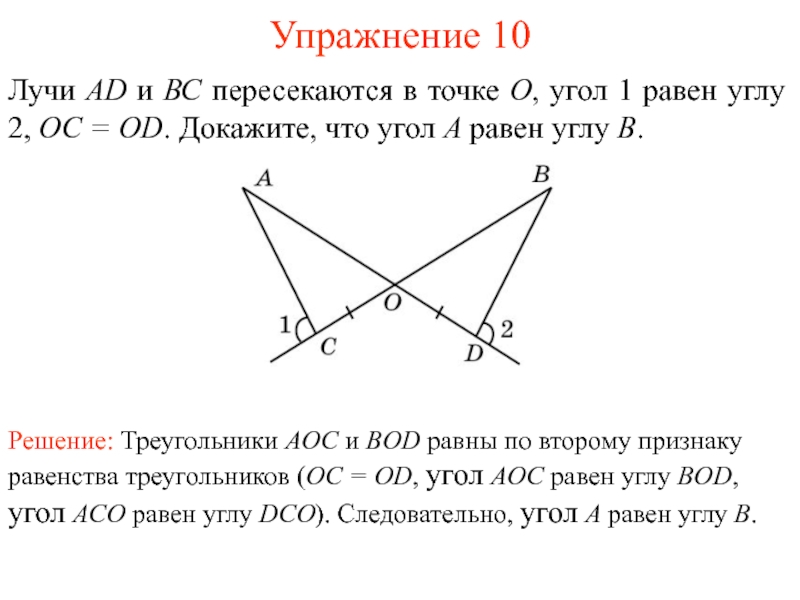
Лучи AD и ВС пересекаются в точке О, угол
1 равен углу 2, OC = OD. Докажите, что угол
A равен углу B.Решение: Треугольники AOC и BOD равны по второму признаку равенства треугольников (OC = OD, угол AOC равен углу BOD, угол ACO равен углу DCO). Следовательно, угол A равен углу B.
Слайд 12Упражнение 11
Лучи AD и ВС пересекаются в точке О, угол
1 равен углу 2, OC = OD, угол A
равен 40о. Найдите угол B.Решение: Треугольники AOC и BOD равны по второму признаку равенства треугольников. Следовательно, угол B равен углу A и равен 40о.
Слайд 13Упражнение 12
Решение: Треугольники ABC и CDA равны по второму признаку
равенства треугольников (AC – общая, угол 1 равен углу 2,
угол 3 равен углу 4). Следовательно, AB = 11 см, BC = 19 см.На рисунке угол 1 равен углу 2, угол 3 равен углу 4. Докажите, что треугольники АВС и CDA равны. Найдите АВ и ВС, если AD = 19 см, CD = 11 см.
Слайд 14Упражнение 13
На рисунке угол DAB равен углу CBA, угол CAB
равен углу DBA, СА = 13 см. Найдите DB.
Решение:
Треугольники ABC и BAD равны по второму признаку равенства треугольников (AB – общая, угол DAB равен углу CBA, угол CAB равен углу DBA). Следовательно, DB = 13 см.
Слайд 15Упражнение 14
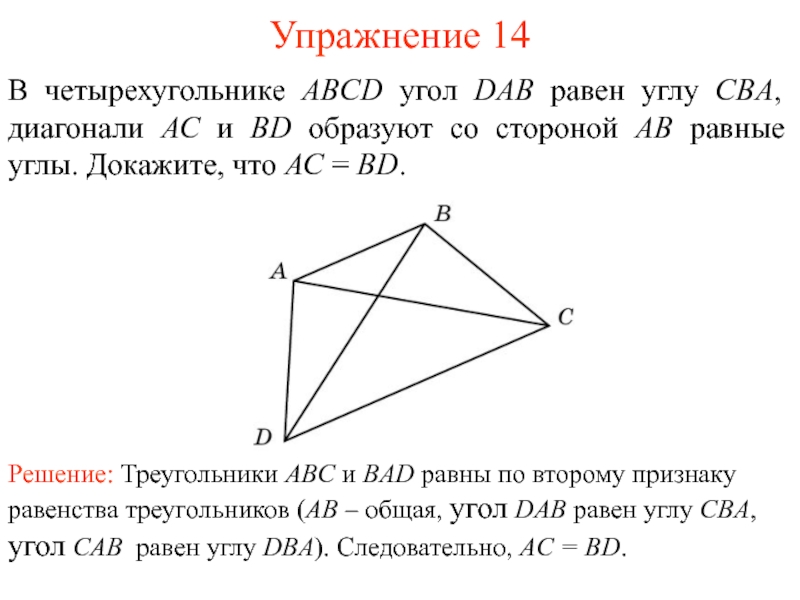
Решение: Треугольники ABC и BAD равны по второму признаку
равенства треугольников (AB – общая, угол DAB равен углу CBA,
угол CAB равен углу DBA). Следовательно, AC = BD.В четырехугольнике ABCD угол DAB равен углу CBА, диагонали АС и BD образуют со стороной АВ равные углы. Докажите, что АС = BD.
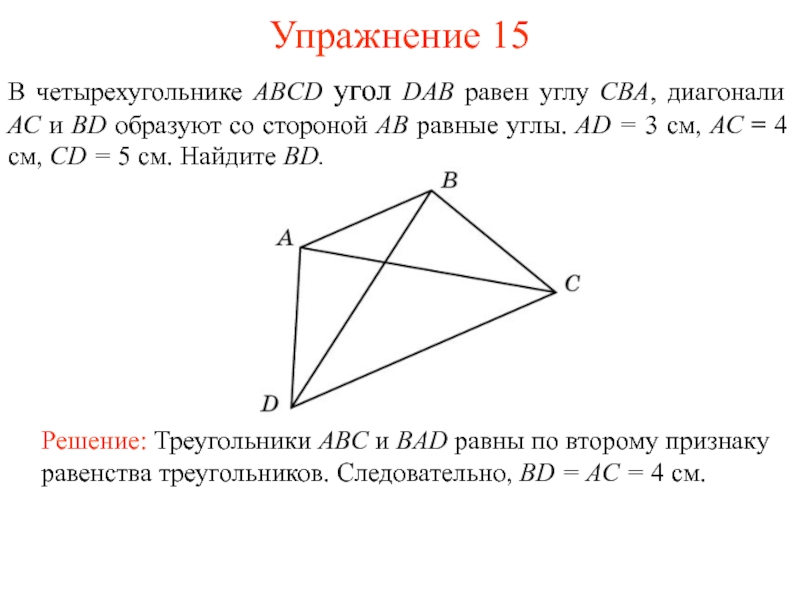
Слайд 16Упражнение 15
В четырехугольнике ABCD угол DAB равен углу CBА, диагонали
АС и BD образуют со стороной АВ равные углы. AD
= 3 см, АС = 4 см, CD = 5 см. Найдите BD.Решение: Треугольники ABC и BAD равны по второму признаку равенства треугольников. Следовательно, BD = AC = 4 см.
Слайд 17Упражнение 16
Треугольники АВС и А1В1С1 равны. Отрезки CD и C1D1
образуют со сторонами соответственно СВ и С1В1 равные углы. Докажите,
что AD = A1D1.Доказательство: Треугольники BCD и B1C1D1 равны по второму признаку равенства треугольников (BC = B1C1, угол CBD равен углу C1B1D1, угол BCD равен углу B1C1D1). Следовательно, BD = B1D1. Из этого и равенства сторон AB и A1B1 вытекает равенство AD = A1D1.
Слайд 18Упражнение 17
На рисунке AE=AC, угол 1 равен углу 2. Докажите,
что треугольники ABC и ADE равны.
Доказательство: Треугольники ABC и ADE
равны по второму признаку равенства треугольников (AC = AE, угол ACB равен углу AED, угол A – общий). 
Слайд 19Упражнение 18
На рисунке AE=AC, угол 1 равен углу 2, угол
A равен 50o, угол B = 40o. Найдите угол D.
Решение:
Треугольники ABC и ADE равны по второму признаку равенства треугольников. Следовательно, угол D равен углу B и равен 40o.
Слайд 20Упражнение 19
Ответ: AHB и CPD, ABC и CDA, CHB и
APD.
На рисунке BH перпендикулярна AC, DP перпендикулярна AC, AH=CP и
угол BAC равен углу ACD. Найдите равные треугольники.
Слайд 21Упражнение 20
По рисунку объясните, как можно найти расстояние от точки
M до недоступной точки N, например дерева на острове.
Решение:
Выбирается какая-нибудь точка M. Откладываются углы KML и MKL, соответственно равные углам NKM и NMK. Искомое расстояние будет равно длине отрезка ML.
