Слайд 1ВВЕДЕНИЕ
Теория активных систем (ТАС) - раздел теории управления социально-экономическими системами,
изучающей свойства механизмов их функционирования, обусловленные проявлениями активности участников системы.
Основным методом исследования в ТАС является математическое (теоретико-игровое) и имитационное моделирование.
За тридцать лет ее развития в ТАС были разработаны, исследованы и внедрены множество эффективных организационных механизмов, соответствующие модели и методы находят применение при решении широкого круга задач управления в экономике и обществе - от управления технологическими процессами до принятия решений на уровне регионов и стран.
Слайд 2ПРОБЛЕМЫ УПРАВЛЕНИЯ
АКТИВНЫМИ СИСТЕМАМИ
Слайд 3Модель активной системы
Рассмотрим общую формулировку задачи управления некоторой активной системой.
Пусть состояние системы описывается переменной y, принадлежащей допустимому множеству A.
Состояние системы в рассматриваемый момент времени зависит от управляющих воздействий u.
Предположим, что на множестве U x A задан функционал Ф(u, y), определяющий эффективность функционирования системы (с точки зрения управляющего органа).
Величина K(u) называется эффективностью управления.
Задача управляющего органа заключается в выборе такого допустимого управления, которое максимизировало бы значение его эффективности при условии, что известна реакция G(u) системы на управляющие воздействия.
Слайд 4Различия в управлении
пассивными и активными системами.
Для пассивной (например,
технической) системы зависимость y = G(u) является, фактически, моделью системы
- управляемого объекта, отражающей законы ее функционирования.
Например, для динамической системы эта зависимость может являться решением системы дифференциальных уравнений, для некоторого черного ящика - быть результатом экспериментов и т.д. Общим для всех пассивных систем является их "детерминизм" с точки зрения управления в смысле отсутствия у управляемого объекта свободы выбора своего состояния, собственных целей, средств их достижения и возможности прогнозировать поведение управляющего органа.
В активных системах (АС), то есть системах, в которых управляемые субъекты обладают свойством активности, в том числе - свободой выбора своего состояния.
Помимо возможности выбора состояния, элементы АС обладают собственными интересами и предпочтениями, то есть осуществляют выбор состояния целенаправленно (в противном случае их поведение можно было бы рассматривать как пассивное).
Одним из важнейших проявлений активности также является способность управляемых субъектов «предсказывать» (в рамках имеющейся информации) поведение управляющего органа – его реакцию на состояние системы и т.д.

Слайд 5Параметры, характеризующие
активную систему
1. Состав АС - совокупность субъектов и
объектов, являющихся элементами системы (в дальнейшем для их обозначения будет
использоваться термин "участники" АС).
2. Структура АС - совокупность информационных, управляющих и других связей между участниками АС, включая отношения подчиненности и разделение прав принятия решений. В большинстве моделей теории активных систем исследовались двухуровневые АС веерного типа, состоящие из одного управляющего органа - центра на верхнем уровне иерархии и одного или нескольких подчиненных ему управляемых субъектов - активных элементов (АЭ) на нижнем уровне.
3. Число периодов функционирования отражает наличие или отсутствие динамики (однократности или многократности выбора стратегий участниками АС в течение рассматриваемого периода времени).
Слайд 64. Целевые функции участников системы, отражающие их интересы и предпочтения.
В формальных моделях ТАС считается, что рациональному поведению участников соответствует
выбор состояний (стратегий), которые максимизировали бы их целевые функции.
5. Допустимые множества состояний (стратегий) участников АС, отражающие индивидуальные и общие для всех ограничения на выбор состояний, накладываемые окружающей средой, используемой технологией и т.д.
6. Порядок функционирования - последовательность получения информации и выбора стратегий участниками АС.
7. Информированность участников - та информация, которой обладают участники АС на момент принятия решений о выбираемых стратегиях.
Слайд 7В широком смысле механизм функционирования (управления) АС - это совокупность
законов, правил и процедур взаимодействия участников системы, которые определяются составом,
структурой, целевыми функциями, допустимыми множествами, предпочтениями, числом периодов функционирования, порядком функционирования и информированностью участников системы.
В узком смысле механизм управления представляет собой совокупность правил принятия решений (ППР) участниками АС при заданных ее составе, структуре и т.д. (например, ППР центра - зависимость u(y), ставящая соответствие состояниям АЭ конкретное значение управляющего воздействия).
Слайд 8Базовая двухуровневая модель
активной системы
Слайд 9Задачи производства продукции
Рассмотрим систему, состоящую из планирующего органа (центра) и
n предприятий-производителей однородной продукции (элементов).
Будем исследовать функционирование системы в
дискретные периоды (месяц, квартал, год).
В каждом из них задача центра — назначить план каждому предприятию при условии, чтобы суммарный выпуск продукции был равен заданному количеству R (плановое задание для системы в целом), а суммарные затраты на производство продукции были минимальными.
Обозначим: xi — план, zi — затраты i-го предприятия на выпуск продукции в количестве xi.
Естественно принять в детерминированных моделях, что при заданном плане xi существует минимальная величина 3i(xi) затрат. Однако реальные затраты могут быть значительно выше этой объективной величины (плохая организация производства, отсутствие заинтересованности предприятия к снижению затрат и т. д.).
Описание модели
Слайд 10Понятно, что 3i(xi) — неубывающая функция xi (затраты растут с
ростом плана).
Для упрощения примем
Параметр ri будем называть коэффициентом эффективности
производства.
Итак, реальные затраты i-го предприятия
Суммарные затраты
Слайд 11Задача центра минимизировать суммарные затраты
при условии
Функцию Ф(z) будем называть целевой функцией центра в рассматриваемом
периоде.
Примем, что при выполнении плана предприятие получает доход
где λ – цена продукции.
Функцию fi будем называть целевой функцией предприятия в рассматриваемом периоде.
Слайд 12Если бы центр знал коэффициенты эффективности {ri} всех предприятий, то
задача оптимального функционирования системы была бы элементарной:
Применяя метод множителей Лагранжа,
выпишем функцию Лагранжа:
,где μ - множитель Лагранжа.
Дифференцируя по х, получим
Определяя μ из условия (2), получим оптимальный план
(1)
(2)
Слайд 13Теперь центру достаточно лишь назначить каждому предприятию план и обеспечить
контроль за его исполнением.
Поскольку при заданном плане xi и цене
λ прибыль предприятия максимальна при минимальных затратах, то предприятие заинтересовано в реализации плана с минимальными затратами
Затраты на выпуск продукции при этом также будут минимальными
Слайд 14 Проблемы возникают в том случае, если центр имеет
ограниченную информацию о коэффициентах эффективности предприятий.
А именно, примем,
что центру известны только границы [d,D]
возможных значений (решение принимается в условиях неопределенности).
В этом случае довольно распространенным является принцип максимального гарантированного результата, который в нашей задаче приводит к выбору плана, обеспечивающего минимальные затраты в наихудших условиях производства, т. е. при минимальных возможных значениях коэффициентов эффективности {ri}.
Слайд 15 Примем для упрощения одни и те же границы [d,D] для
всех предприятий.
Решая задачу оптимального планирования при значениях r =
d, получим план
со значением целевой функции системы
т. е. с точки зрения центра все предприятия находятся в равных условиях, и поэтому плановое задание распределяется поровну.
Слайд 16 Относительное увеличение затрат в плане
по сравнению с оптимальным планом зависит от
{ ri }, неизвестных центру.
Чтобы получить оценку, не зависящую от { ri } найдем минимум этого выражения при всевозможных d ≤ ri ≤ D.
Минимум Φm/Φ0 соответствует случаю, когда ri принимают одно из крайних значений: либо ri = d, либо ri =D.
Пусть k – число АЭ, для которых ri = D,
тогда n-k - число АЭ, для которых ri = d.
Слайд 17 Минимум Φm/Φ0 достигается при k=n/2, если n – четно,
и k=(n±1)/2,
если n – нечетно.
Окончательно получаем
Нечеткие представления центра о коэффициентах эффективности
предприятий сильно снижают эффективность управления:
при ξ=0,5 (D= 2d) Φm/Φ0 =0,89;
при ξ=0,1 (D=10d) Φm/Φ0 =0,33.
Слайд 18Принцип жесткой централизации
Если центр обязывает предприятия сообщать оценки коэффициентов эффективности,
то способ формирования данных называется встречным, поскольку информация движется «снизу
вверх», а планы назначаются «сверху вниз».
Обозначим
si·- оценку коэффициента эффективности, сообщаемую ί-м предприятием,
s={si}—совокупность всех оценок.
Центр на основе полученной информации назначает предприятиям планы {xi(s)} и устанавливает цену λ(s) продукции.
Процедура π(s) = {λ(s) , x(s)} определения планов и цены называется законом управления.
x(s) - закон планирования,
λ(s) - зaкон ценообразования.
Слайд 19Законы управления определяются, как правило, на основе
тех или иных принципов
управления.
Принцип жесткой централизации характеризуется тем, что центр в первую
очередь учитывает интересы системы.
Для рассматриваемого нами случая этот принцип соответствует решению центром задачи оптимального планирования
Выбор закона ценообразования в данном случае произволен.
Его конкретизация определяет некоторый закон жесткой централизации.
Ее оптимальное решение определяет закон планирования
Слайд 20Рассмотрим простейший вариант, когда цена λ фиксирована
Подставляя закон планирования xi(s)
в целевую функцию предприятия, выразим ее как функцию сообщаемых оценок
{si}:
Анализ целевой функции предприятия показывает, что прибыль предприятия зависит не только от его оценки, но и от оценок всех остальных предприятий.
К анализу функционирования системы в этом случае естественно применить теоретико-игровой подход. Мы имеем дело с типичной игрой n лиц (предприятий) с функциями выигрыша i-гo игрока (предприятия) fi(s).
Оценка si является стратегией i-гo игрока, а отрезок [d, D] — множеством возможных стратегий.
Совокупность оценок s= {si} определяет ситуацию игры.
Под решением игры будем понимать ситуацию
равновесия в смысле Нэша (точка Нэша), т. е. ситуацию s* такую, что
Слайд 21Равновесие Нэша является одной из наиболее часто используемых концепций равновесия.
Вектор yN={y1N, … ,ynN} называется равновесием Нэша
(точкой Нэша), если
i I , yi Ai fi (yiN , y-iN) fi (yi , y-iN) ,
то есть никому из активных элементов не выгодно изменять свою стратегию, при условии, что остальные АЭ не меняют своих стратегий.
Следует отметить, что использование концепции равновесия Нэша требует введения следующей гипотезы: игроки не могут договориться и уйти из этой точки сообща, то есть равновесие Нэша предполагает отсутствие коалиций игроков (то есть рассматриваются бескоалиционные игры).
Слайд 22Для поиска решения игры (равновесия Нэша), отметим, что максимум целевой
функцию предприятия fi достигается при условии xi = λri (в
дальнейшем обозначим λri = vi - оптимальный план с точки зрения предприятия).
Кроме того, xi(s) = si R/S является возрастающей функцией si.
Поэтому,
если xi(s) < vi , то si* = D ,
если xi(s) > vi , то si* = d.
Наконец, если d > si* > D , то обязательно xi*= xi (s) = vi .
Примем, что предприятия упорядочены .
Рассмотрим 5 возможных случаев:
Слайд 23
Рассмотрим 5 возможных случаев.
1. Предложение на выпуск продукции со стороны
предприятия ∑vi значительно превышает спрос R
nvi ≥ R, ∑vi >
R
Единственная ситуация равновесия
Слайд 242. Предложение на выпуск продукции со стороны предприятия ∑vi
превышает спрос R
nvi < R < ∑vi
Определим минимальное k такое,
что для 0 < k < n выполняется условие
В таком случае равновесие по Нэшу достигается при следующих стратегиях:
Слайд 253. Баланс спроса R и предложения на выпуск
продукции со стороны предприятия ∑vi
∑vi = R
В таком случае равновесными
стратегиями являются
где γ – некоторый параметр, определяемый условием:
Слайд 264. Спрос R превышает предложение на выпуск продукции со
стороны предприятия ∑vi
∑vi ≤ R < nvi
Определим минимальное k такое,
что для 0 < k < n выполняется условие
В таком случае равновесие по Нэшу достигается при следующих стратегиях:
Слайд 275. Значительно спрос R значительно превышает предложение на выпуск
продукции со стороны предприятия ∑vi
nvi ≤ R, ∑vi
R
Единственная ситуация равновесия
Слайд 28Заметим, что для случаев 1) (сильный избыток предложения продукции) и
5) (сильный дефицит продукции) план в ситуации равновесия совпадает с
полученным при использовании только имеющейся информации о границах [d, D]. Поэтому и эффективность законов ЖЦ будет не выше, чем К0. Эти случаи являются самыми неблагоприятными режимами работы системы с точки зрения ее эффективности.
Таким образом, в этих двух случаях дополнительная информация не дает эффекта, поскольку сообщаемые оценки равны граничным значениям D или d соответственно и, по существу, не несут новой информации для центра.
Слайд 29Эффективность рассмотренного закона ЖЦ можно повысить, если ввести штрафы за
искажение информации.
Пусть на этапе реализации центр может оценить реальные
затраты на выпуск продукции и тем самым реально достигнутое значение эффективности
ai = xi2/2zi < ri.
Это позволяет ввести в целевую функцию составляю-щую, соответствующую штрафу при отклонении аi от сообщенной оценки si. Мы рассмотрим случай «сильных штрафов», когда единственной разумной стратегией предприятия является совпадение реальной аi и планируемой эффективности si. При этом
zi = xi2/2ai = xi2/2si
и целевая функция предприятия i примет вид
Слайд 30Если λ ≥ R/2S, то s* = r —
единственная ситуация равновесия.
При этом оба сомножителя — возрастающие функции
si и, следовательно, fi(s) также возрастающая функция si. Поэтому ее максимум достигается на границе si* = ri .
Таким образом, установив достаточно высокую цену продукции, центр может обеспечить оптимальное функционирование системы (в смысле минимума затрат на производство продукции), т. е. К0 = 1. Для этого достаточно взять λ =R/2nd .
Однако цена продукции при малых значениях d может быть значительно большей, чем λ =R/2H. Если же λ
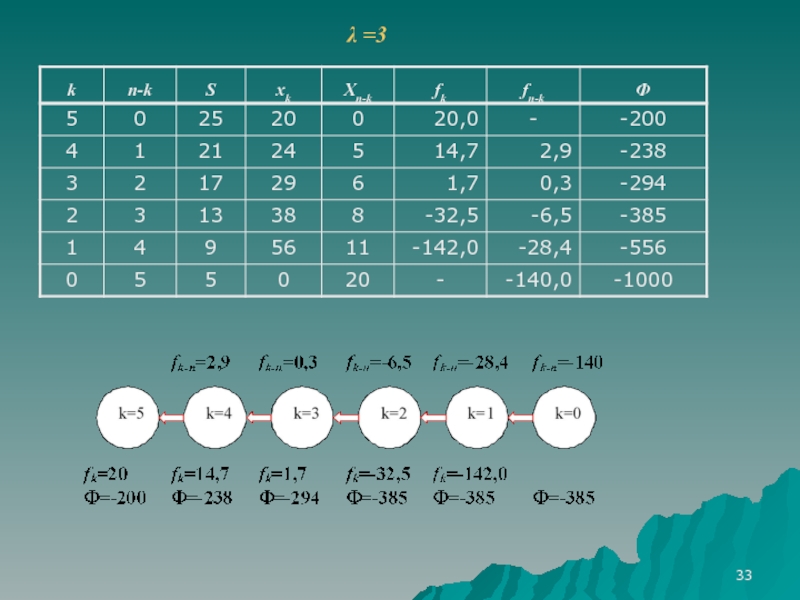
Слайд 31Пусть n=5, R=100, λ=1, d=1, ri=5 i=1÷5, H=∑ri =25,
имеем
λ=1 < R/2H=2.
Если все предприятия сообщают достоверные
оценки, то
Если одно из предприятий сообщит минимальную оценку, то
Анализ ситуации показывает, что в этих условиях каждому предприятию выгодно сообщать минимальную оценку si=1 при условии, что все остальные предприятия сообщают достоверные оценки, т. е. ситуация s* = r не является точкой Нэша.
Проведем анализ ситуаций, в которых определенное число k предприятий сообщают достоверные оценки, а остальные (n—k) —минимальные оценки.
Слайд 34Принцип открытого управления
Причина низкой эффективности принципа ЖЦ (при фиксированной цене
продукции) заключается в определенном противоречии интересов центра и предприятий.
Суть
этого противоречия в следующем. Центр планирует выпуск продукции в количестве R, а предприятия в сумме «желают» выпускать V = Σ vi = λ H. Если R ≠ λ H, то цели центра и предприятий не совпадают, и никакая процедура планирования этого конфликта не разрешит.
Понятно, что предприятия, преследуя свои цели (в данном
случае, желая получить «выгодные» планы vi), пользуются предоставленной им свободой в предоставлении информации центру.
Возникает идея согласовать интересы центра и предприятий.
Слайд 35Примером такого согласования является случай 3) анализа принципа жесткой централизации.
В этом случае Σ vi = R, т. е. цели
центра и предприятий совпадают. Противоречия нет, а значит, и нет причин искажать данные.
Действительно, как показывает анализ, ситуации равновесия имеют вид s* = ·r. Учитывая моральный
стимул «сообщать достоверные сведения» при прочих равных условиях, можно принять, что предприятия будут сообщать достоверные оценки.
Итак, для разрешения конфликта достаточно
установить цену λ = R/H. Трудность здесь в том, что величины Н центр не знает (т. е. знает только, что nd
Слайд 36Для этого определим закон управления
Заметим, что при таком определении
x(s) , план xi обеспечивает максимум функции λxi-1/2si ·хi2 отражающей
представление центра об интересах предприятия. Будем называть ее функцией предпочтения предприятия.
Таким образом, при указанном законе управления каждое предприятие получает план, обеспечивающий максимум его функции предпочтения. Такой план будем называть согласованным.
Принцип управления, при котором все предприятия получают согласованные планы, назовем принципом открытого управления (ОУ).
(1)
Слайд 37Формально принцип ОУ можно записать в виде следующей задачи оптимизации:
определить x≥0, λ≥0 такие, что
(2)
(3)
Задача (2)-(3) называется задачей согласованного управления,
а условия (3) условиями совершенного согласования
Слайд 38Проведем анализ полученного закона ОУ, т. е. определим точки Нэша
соответствующей игры. Подставляя закон управления (1) в целевые функции предприятий,
получим
Выпишем уравнения для определения ситуации равновесия, предполагая, что
Несложные преобразования приводят к следующей системе уравнений
Если для некоторого предприятия si*< d, то следует принять si*= d.
Слайд 39Отклонение точки Нэша s* от достоверного значения вектора r можно
оценивать величиной степени достоверности информации
Учитывая, что Si*≥(n-1)d , ri≤D ,
ξ = d / D, получим
Очевидно, что и, следовательно si*≈ ri, ; xi ≈ xi, ; KОУ ≈ 1.
Таким образом, при достаточно большом числе предприятий закон ОУ является квазиоптимальным законом управления, обеспечивая близость равновесного плана к оптимальному.
Дополнительно, сообщаемая информация близка к достоверной.
Цена продукции в этой ситуации
Слайд 40Рассмотрим случай, когда в системе имеется одно предприятие, коэффициент эффективности
которого значительно выше, чем у других предприятий.
Пусть это первое предприятие,
т. е. r1>ri , i=2÷n. Тогда при
достаточно большом числе предприятий si*≈ ri , i=2÷n и
Для оценки эффективности функционирования системы определим
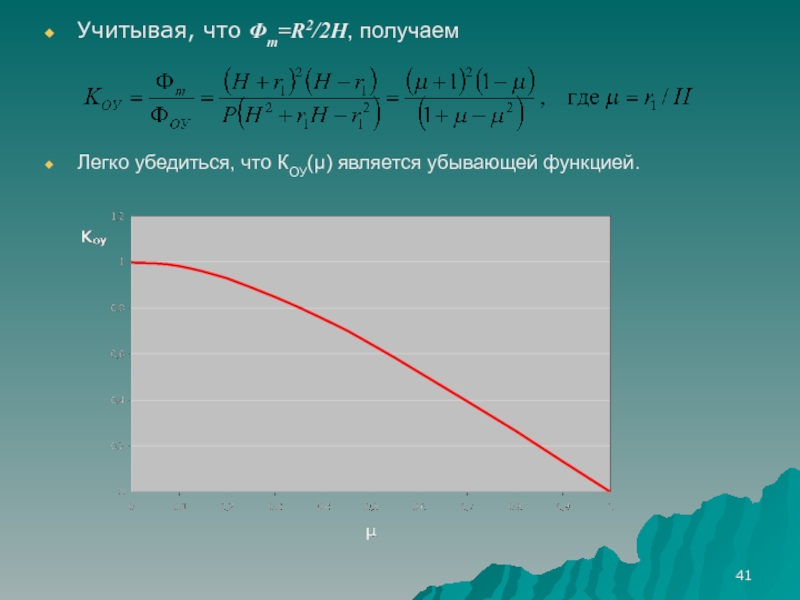
Слайд 41Учитывая, что Φm=R2/2H, получаем
Легко убедиться, что КОУ(μ) является убывающей функцией.
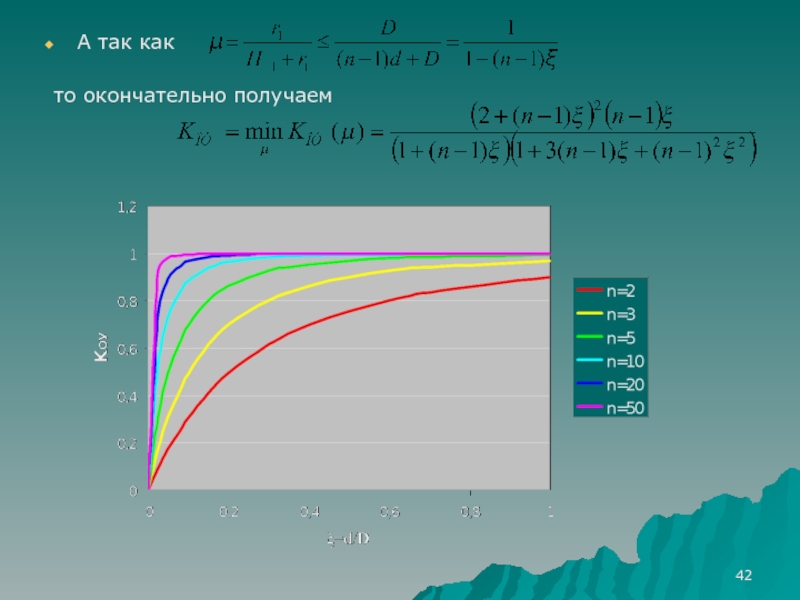
Слайд 42А так как
то окончательно получаем
Слайд 43При малых ξ эффективность открытого управления
в сравнении
с эффективностью жесткого централизованного управления
оказывается примерно в (n-1)
раз выше
Слайд 44Предположим, эффективность первого предприятия, назовем его монополистом, значительно выше суммарной
эффективности остальных. При достаточно большом числе предприятий имеем
Таким образом,
монополист в положении равновесия выпускает почти половину всей продукции, в то время как в оптимальном плане – почти всю продукцию.
Сообщая заниженную оценку коэффициента эффективности (s1*≈H1<
и получая при этом «сверхприбыль»
- цена, устанавливаемая центром при достоверной информации
Слайд 45Предыдущий анализ показал, что хотя закон ОУ эффективнее закона ЖЦ,
но при малом числе предприятий, а особенно при наличии монополиста
в системе, эффективность закона ОУ может быть весьма низкой.
Здесь существует еще одна опасность— образование коалиции, когда несколько предприятий договариваются о совместных действиях.
Пусть, например, множество Q предприятий договорились сообщать оценки
где - фиксированный коэффициент.
Тогда суммарная оценка коалиции
Суммарный план выпуска коалиции —
Заметим, что производство продукции xQ распределяется в коалиции оптимальным образом (прямо пропорционально коэффициентам эффективности), поэтому суммарные затраты предприятий, входящих в коалицию, равны
Слайд 46Коалиция выступает как одно предприятие с эффективностью HQ. Если HQ>>H/2
, то коалиция выступает как монополист.
Следует подчеркнуть, что коалиция в
данном случае является объединением на информационном уровне (члены коалиции договариваются только о величине , например, = 0,25 — занизить в 4 раза сообщаемую оценку).
Ниже мы покажем, что в условиях централизованного планирования можно предложить законы управления достаточно эффективные и при наличии монопольной организации (например, отрасли, специализирующейся на данном виде продукции).
Слайд 47Пример.
Пусть n = 2, r1 = 1, г2=9, d=1,
D=100.
s1*=s2*=d=1.
x1=x2=R/2.
Затраты в системе равны Фоу=5/36 *R2.
Минимальные затраты Фm
= R2/20.
Эффективность закона ОУ в данном случае равна 0,36.
Слайд 48Дифференцированные цены
Введем индивидуальные цены i продукции для каждого предприятия
следующим образом:
(4)
где .
Очевидно, что центр не может определять i на
этапе планирования, так как цена зависит от реальной эффективности аi. Центр вычисляет норматив Si и сообщает его предприятию i. Цену i предприятие определяет самостоятельно на этапе реализации по формуле ценообразования (4).
Подставляя закон планирования
и закон ценообразования (4) в целевую функцию предприятия, получим
(5)
Слайд 49Заметим, что из
следует, что
Дифференцируя (5) по
si , получаем уравнение для определения равновесной стратегии si*
Его единственное
решение si*=ai.
Подставляя в (5), получаем
где
Слайд 50Анализ равновесной ситуации показывает, что
при отсутствии монополистов (r1
совпадает с оптимальной;
при наличии монополиста (r1
оптимальной. При этом, чем выше уровень монополизации, тем менее эффективно применение дифференциальных цен.
Слайд 51Адаптивный способ формирования данных
При адаптивном способе формирования данных оценка
si параметра ri определяется на основе известных планов, затрат и
оценок в предыдущие периоды функционирования. Примем, что
где xi,k-1 , zi,k-1 – план и затраты i-го АЭ в периоде k-1;
si,k – оценка коэффициента эффективности производства в периоде k.
В этом случае выбор предприятием конкретной величины затрат в данном периоде функционирования, очевидно, повлияет на план и цену продукции в будущие периоды.
Одним из свойств активности организаций является учет последствий принимаемых «сегодня» решений.
Слайд 52Для формализации этого свойства примем, что интересы предприятия в рассматриваемом
периоде (будем считать, что это период с номером 0) определяются
стремлением к максимуму взвешенной суммы прибылей в данном и будущих периодах
(7)
где δik — дисконтирующий множитель, (0≤ δik <1, будущие прибыли учитываются «сегодня» с меньшим весом). Выражение (7) будем называть критерием эффективности с учетом будущих периодов.
Заметим, что выбор zi,0 по существу, эквивалентен выбору достигнутого коэффициента эффективности
который и принимается за оценку si,1 следующего периода. Выбор ai мы и будем считать стратегией i-го предприятия в рассматриваемом периоде (очевидно, что d ≤ ai ≤ ri).
Слайд 53Для упрощения примем следующую гипотезу поведения предприятие предполагает, что достигнутая
эффективность аi останется неизменной в будущие периоды. Следовательно, и оценка
si,k будет равна аi для всех k≥1.
При сделанных предположениях критерий эффективности (7) примет вид
где - степень дальновидности предприятия.
Подставляя закон ОУ: i=R/A; xi=ai*R/A ,получим окончательно
(8)
Слайд 54Ситуацию равновесия а* называется устойчивой по периодам функционирования, если xi(a*)=xi,0
, i=1÷n.
Для ее определения продифференцируем (8) по ai
Откуда
При δ→1 мы
имеем Ni→∞, т.е. высокая дальновидность позволяет существенно поднять эффективность АЭ.
Учитывая, что чем меньше Ni, тем ближе ai* к ri, можно сделать вывод о большей эффективности закона ОУ при адаптивном способе формирования данных, если степень дальновидности монополиста не бесконечна.
Следует, однако, отметить, что определение устойчивой по периодам функционирования ситуации равновесия потребовало дополнительных гипотез о поведении предприятий в будущие периоды, и представляется поэтому менее естественным, чем определение точки Нэша при встречном способе формирования данных.
Слайд 55Стимулирование и соревнование
Рассмотрим несколько иную постановку задачи производства продукции.
Примем, что цель центра — максимизировать суммарный выпуск продукции. Планирование
происходит на основе встречного способа формирования данных, причем предприятия сообщают непосредственно планы xi выпуска продукции сверх основного задания (встречные планы), которые и утверждаются центром. Как и ранее, предполагаем, что эти планы будут выполнены. В распоряжении центра имеется фонд материального поощрения М, который он распределяет между предприятиями в зависимости от показателей их работы {xi}. Мы рассмотрим два механизма распределения фонда — стимулирование и соревнование.
Слайд 56Механизм стимулирования заключается в распределении фонда прямо пропорционально xi т.
е. часть фонда Фi(х), получаемая предприятием i, равна
(9)
Механизм соревнования заключается в определении места, занятого предприятием в соревновании и премировании в зависимости от занятого места. Целевая функция предприятия равна
(10)
где 3i (xi) — затраты на выпуск продукции xi.
Слайд 57Анализ механизма стимулирования.
Пусть 3i(xi)=kixi (ki>0). Целевая функция предприятия
(11)
Определим ситуацию равновесия (в смысле Нэша), предполагая
После некоторых вычислений получим
(12)
Слайд 58Анализ механизма соревнования.
Место, занятое предприятием в соревновании, определяется в
зависимости от принятого им плана xi. Пусть xi упорядочены по
убыванию (х1 ≥ х2 ≥ ... ≥ хn). Тогда номер предприятия соответствует занятому им месту (для определенности считаем, что при xi = xi+1 лучшее место занимает предприятие с меньшим номером). Целевая функция предприятия
(13)
Сложность исследования механизма соревнования в том, что равновесия Нэша в данном случае не существует. Необходимо определить решение игры, исходя из разумных гипотез о поведении предприятий.
Примем k1≤k2≤...≤kn. В этом случае предприятие с меньшим номером находится в лучших условиях и, естественно, в устойчивой ситуации будет занимать лучшее место. Приняв такое предположение о распределении мест, найдем устойчивые в некотором смысле планы xi*.
Слайд 59Очевидно, хn* =0. Если x*n-1
приняв план x*n-1
свой выигрыш (cn-knхn>0). Поэтому для устойчивого удержания (n—1) места предприятие (n—1) должно принять план
Его выигрыш при этом
Аналогично для удержания места (n—2) предприятие (n—2) должно принять план не менее
(если хn-2< х*n-2 , то предприятие (n — 1), приняв план х„-2 < xn-1 < x*n-2 , займет место (n—2) и увеличит свой выигрыш).
Слайд 60Продолжая таким образом, получим
Ситуация х* является устойчивой в следующем смысле.
Любому предприятию i невыгодно занимать более высокое место (т. е.
с меньшим номером), если остальные предприятия не меняют своих планов. С другой стороны, принимая план меньше x*i предприятие рискует потерять место (получить меньший выигрыш).
Принимая ситуацию равновесия х* за решение игры, оценим суммарный выпуск продукции
Эта величина зависит от ki , неизвестных центру.
Слайд 61Для сравнения с механизмом стимулирования оценим гарантированное значение
Если (i-1)
Δi ≤ i Δi+1 ( i=2÷n ), то минимум достигается
при значении
и равен
Слайд 62Поставим задачу определить распределение премий {ci} (а следовательно и {Δi
} ), обеспечивающее максимальный суммарный выпуск продукции X*(Δ).
Из условия
получаем .
Максимум достигается при условии и равен
(14)
Сравнивая (12) и (14), видим, что механизм соревнования эффективнее механизма стимулирования при правильно выбранном распределении премий.
Слайд 63Задачи распределения ограниченного ресурса
ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ [optimal resource allocation] —
такое распределение ограниченных ресурсов, которое обеспечивает их наилучшее использование с
точки зрения заданного критерия оптимальности. Задачи оптимального распределения ресурса (распространено также несколько более широкое понятие — эффективное распределение ресурсов) решаются с помощью моделей линейного и нелинейного программирования, с конечным и бесконечным числом входов и выходов, моделей свободной конкуренции (конкурентного рыночного равновесия), моделей с централизованной и децентрализованной информацией и др.
За “вклад в теорию оптимального распределения ресурсов” в 1975 г. были награждены Нобелевской премией основоположники этого направления Л. В. Канторович и Т. Купманс.
Слайд 64Канторович Леонид Витальевич (1912-1986), советский математик и экономист, академик АН
СССР (1964), лауреат Нобелевской премии по экономике (1975).
Первооткрыватель метода
линейного программирования и признанный глава экономико-математического направления экономической науки в СССР.
Окончил Ленинградский университет (1930). Работал профессором Ленинградского университета с 1934 по 1960 г., руководителем математико-экономической лаборатории и заместителем директора Института математики Сибирского отделения АН СССР в Новосибирске, затем в Москве, в Институте системных исследований, Институте управления, Академии народного хозяйства.
Нобелевской премии удостоен вместе с Т. Купмансом “за вклад в теорию оптимального распределения ресурсов”.
Слайд 65Тьяллинг Чарльз Купманс (Tjalling Charles Koopmans; 28 августа 1910, Гравеланд,
Нидерланды - 26 февраля 1985, Нью-Хейвен, Коннектикут, США) — американский
экономист и математик голландского происхождения, лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов».
Учился в Утрехтском университете.
Докторскую степень получил в Лейдене.
Работал в Принстонском, Нью-Йоркском, Чикагском и Йельском университетах. Президент Эконометрического общества (1950).
Президент Американской экономической ассоциации в 1978 году.
Слайд 66За последние десятилетия на Западе развиваются информационные и мотивационные аспекты
теории оптимального распределения ресурса . Это означает, что, во-первых, оптимальное
(эффективное) распределение не возможно без полноценной информации, прежде всего о ценах и рынках и, во-вторых, при распределении ресурсов решающую роль имеют стимулы, которыми руководствуются его участники. Эти стимулы совершенно различны в условиях централизованного планирования и конкурентного рынка.
Слайд 67Механизмы распределения ресурса составляют обширный и чрезвычайно важный с точки
зрения практических приложений класс механизмов управления АС с сообщением информации.
При
их изучении решаются два основных вопроса - синтеза механизма максимальной эффективности и исследования манипулируемости механизмов планирования, то есть возможности построения для них эквивалентных прямых механизмов.
Механизмы распределения ресурса включают в себя приоритетные, конкурсные и другие механизмы, кратко рассматриваемые ниже в настоящем подразделе.
Слайд 68 Неманипулируемые механизмы распределения ресурса
Приведем постановку задачи распределения ресурса в
двухуровневой АС.
Пусть в распоряжении центра имеется ресурс в количестве R.
Задача распределения ресурса подразумевает нахождение такого его распределения между АЭ, которое максимизировало бы некоторый критерий эффективности - например, суммарную эффективность использования ресурса активными элементами.
Если эффективность использования ресурса конкретным АЭ не известна центру, то он вынужден использовать сообщения АЭ, например, о требуемых количествах ресурса.
Понятно, что, если имеется дефицит ресурса, то возникает проблема манипулируемости - АЭ могут сообщать центру недостоверную информацию, стремясь получить оптимальное для себя количество ресурса.
Слайд 69Пусть АЭ сообщают центру информацию si [0;Di] - заявки
на ресурс.
Центр на основании сообщенной ему информации назначает АЭ
планы (выделяет ресурс)
xi = πi(s,R),
где
π i - процедура распределения ресурса (планирования);
i[1;n];
n - число приоритетных направлений.
Пусть ri соответствуют приоритету проекта в некоторой шкале.
Предположим, что выполнена гипотеза дефицитности:
а относительно процедуры распределения ресурса будем считать, что πi(s,R) - непрерывны, строго монотонно возрастают по si и R и строго монотонно убывают по sj, j ≠i;
Весь ресурс распределяется полностью:
Слайд 70Механизм пропорционального
распределения
Классическим примером механизма распределения ресурса является механизм пропорционального распределения:
Указанный
механизм распределения ограниченного ресурса не является неманипулируемым, так как всем
предприятиям выгодно завышать объем заявок до максимально разрешенной величины Di.
В этом случае равновесие достигается при
В частности, при
Слайд 71Механизм абсолютных приоритетов
где - общий для всех проектов коэффициент,
определяемый из условия полного распределения ресурса
Анализ механизма пропорционального распределения показывает,
что в нем наиболее приоритетный проект без дополнительного вмешательства центра получит такое же количество ресурса, как и наименее приоритетный проект.
В связи с этим целесообразно ввести дополнительное ограничение величины выделяемого ресурса в процедуре его распределения пропорционально приоритету проекта:
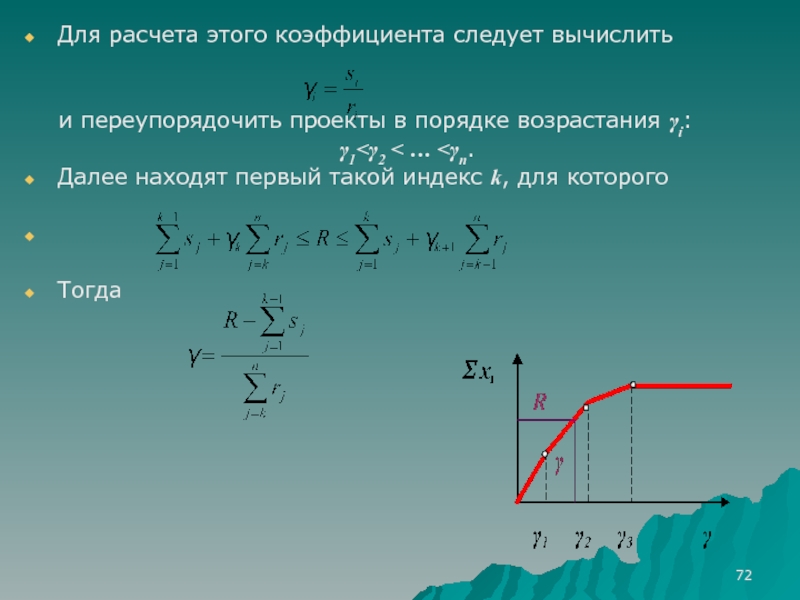
Слайд 72Для расчета этого коэффициента следует вычислить
и переупорядочить проекты в порядке возрастания i:
1<2 < … <n.
Далее находят первый такой индекс k, для которого
Тогда
Слайд 73Равновесие в механизме прямых приоритетов достигается при условии
Указанный механизм позволяет
урезать необоснованное завышение затребованного объема финансирования, однако не стимулирует предприятия
к ограничения величины заявок. По этой причине он не находит практического применения.
Слайд 74Механизм обратных приоритетов
Идея механизма обратных приоритетов заключается в том, что
при распределении ограниченного ресурса учитывается показатель эффективности проекта, то есть
отношение полезного эффекта к выделяемым финансовым средствам. Другими словами, если в двух равнозначных проектах запрашивается разное количество финансовых средств, то предпочтение отдается тому проекту, который требует меньший объем финансирования, так как он будет использовать получаемые средства с большей отдачей.
Слайд 75В этом случае функция распределения средств имеет вид
где -
общий для всех проектов коэффициент, определяемый из условия
полного распределения ресурса
Следует отметить, что механизм обратных приоритетов создает обратную тенденцию - снижать (а не завышать) оценки потребности в ограниченном ресурсе (можно сказать, что в данном случае действует принцип «меньше просишь - больше получишь»), то есть тенденцию экономить, что весьма важно в условиях дефицита средств.
Слайд 76Найдем равновесные стратегии в механизме обратных приоритетов
Очевидно, что в ситуации
равновесия должно выполняться условие:
Перепишем систему в виде
Извлекая корень из
обеих частей этих уравнений, и просуммировав их, получим
Отсюда легко получить
Единственная ситуация равновесия определяется
выражением
Слайд 77Механизм конкурсного распределения финансовых средств
Конкурсные механизмы - один из достаточно
хорошо известных принципов управления в практике регулирования экономическими системами.
Особенность
конкурсных механизмов состоит с том, что они требуют организации явного соперничества между участниками конкурса.
Участники конкурса сообщают в заявке сумму средств и величину экономического или иного эффекта в случае полной реализации проекта.
В число победителей конкурсов входят те исполнители, которые имеют наибольшие показатели эффективности использования выделяемых средств на выполнение работ.
Слайд 78Задача Центра заключается в таком распределении имеющихся финансовых средств, чтобы
полученный от выполнения проектов эффект в системе в целом был
наибольшим. Величина этого эффекта зависит от того, насколько эффективно будут использованы финансовые средства исполнителями и сколько средств будет выделено каждому исполнителю.
Задача участников конкурса заключается в том, что зная принципы определения победителей конкурса и процедуры распределения Центром финансовых средств между исполнителями, выбрать такую стратегию поведения, то есть сообщать в Центр такую информацию о себе, обрабатывая которую Центр выделил бы исполнителю столько финансовых средств, которое обеспечило бы ему получение наибольшего значения целевой функции.
Слайд 79Под конкурсными механизмами будем понимать механизмы распределения финансовых средств, в
котором процедура планирования включает этап определения множества Q проектов-победителей конкурса.
Победители
конкурса получают требуемые средства в полном объеме. Участники конкурса, не вошедшие в группу победителей, получают некоторую заранее фиксированную сумму средств.
Алгоритм определения множества победителей конкурса Q может быть представлен следующим образом. Упорядочим оценки эффективности исполнителей проектов по убыванию
q1 > q2 > ...> qn ,
где
qi = wi /si – эффективность проекта;
wi - экономический эффект;
si - финансовые средства.
Слайд 80Процедура распределения финансовых средств состоит в том, сначала всем проектам
выделяется гарантированная часть ресурса с. Затем проектам, имеющим более высокие
показатели эффективности, выделяются средства в количестве xi - c до тех пор, пока для этого хватает ресурса R. Пусть таких проектов окажется m. После определения множества победителей возможно, что весь ресурс еще не распределен. Этот остаток средств выделяется m+1 участнику конкурса.
Таким образом, функция распределения имеет вид
здесь
n – количество участников конкурса;
m – количество победителей конкурса;
R – финансовые ресурсы, распределяемые по конкурсу;
c – фиксированная премия участнику конкурса.
Слайд 81Рассмотренный вариант конкурсного распределения ресурса отличается тем, что победители конкурса
получают запрошенные средства в полном объеме.
Однако в конкурентной борьбе за
ресурс они могут, с одной стороны, снижать заявку на ресурс si, с другой стороны, завышать эффективность проекта wi. Причем второй способ является для предприятия более предпочтительным.
Для предотвращения этого негативного явления возможна предварительная экспертиза оценки эффективности проектов, представленных, на конкурс.
Другим возможным барьером является контроль выполнения проекта с теми или иными штрафными санкциями за недостижение заявленной эффективности. Можно показать, что в случае сильных штрафных санкций, превышающих выгоды от получения финансирования, возможно появления равновесия, принуждающего игроков вести честную игру.













![ВВЕДЕНИЕ Примем для упрощения одни и те же границы [d,D] для всех Примем для упрощения одни и те же границы [d,D] для всех предприятий. Решая задачу оптимального планирования при](/img/thumbs/00954461f784811d5783a39fb0398176-800x.jpg)










































![ВВЕДЕНИЕ Задачи распределения ограниченного ресурсаОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ [optimal resource allocation] — такое Задачи распределения ограниченного ресурсаОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ [optimal resource allocation] — такое распределение ограниченных ресурсов, которое обеспечивает их](/img/thumbs/a2d62c55a34cf268098b7d862aa17486-800x.jpg)





![ВВЕДЕНИЕ Пусть АЭ сообщают центру информацию si [0;Di] - заявки на Пусть АЭ сообщают центру информацию si [0;Di] - заявки на ресурс. Центр на основании сообщенной ему](/img/thumbs/6251edf918a5abd2493d42bd08622f93-800x.jpg)