Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в комбинаторную логику
Содержание
- 1. Введение в комбинаторную логику
- 2. ЛогикаЛОГИКАКомбинаторнаяПоследовательностнаяПреобразование кодовЛогика с памятью
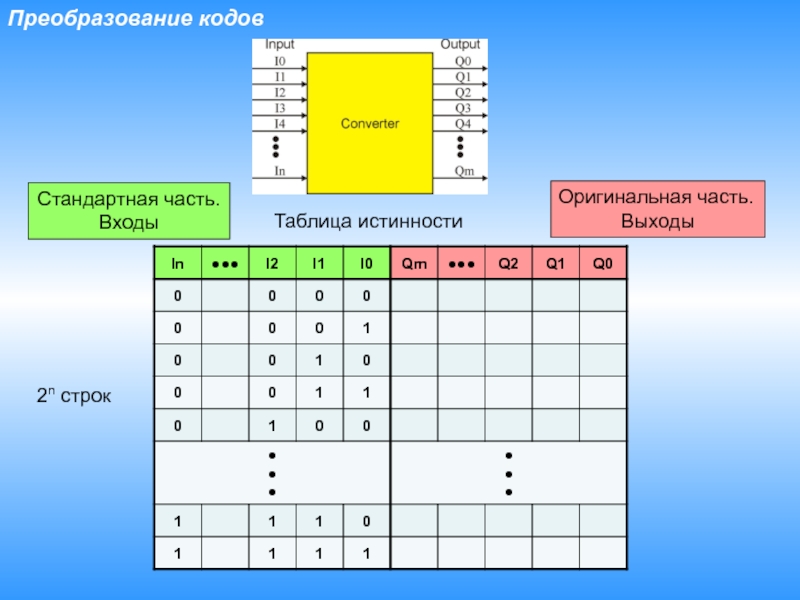
- 3. Преобразование кодовТаблица истинностиОригинальная часть.ВыходыСтандартная часть.Входы2n строк
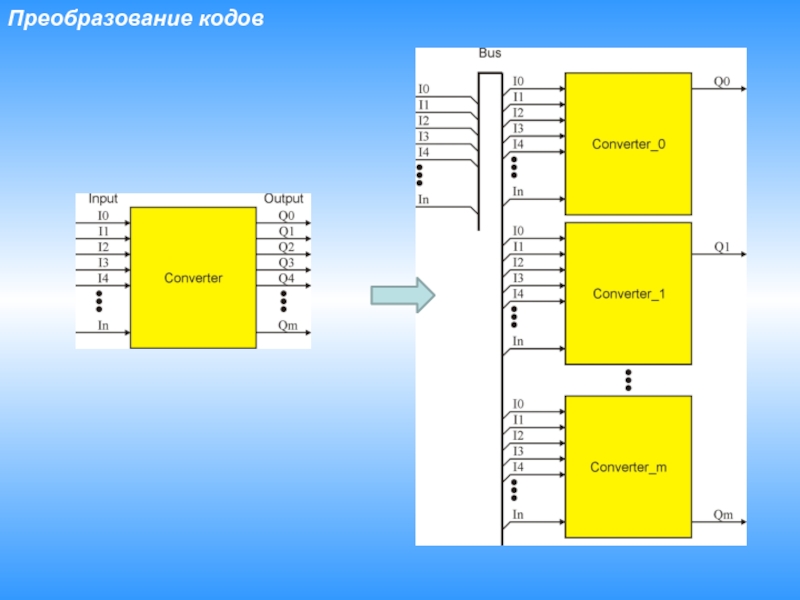
- 4. Преобразование кодов
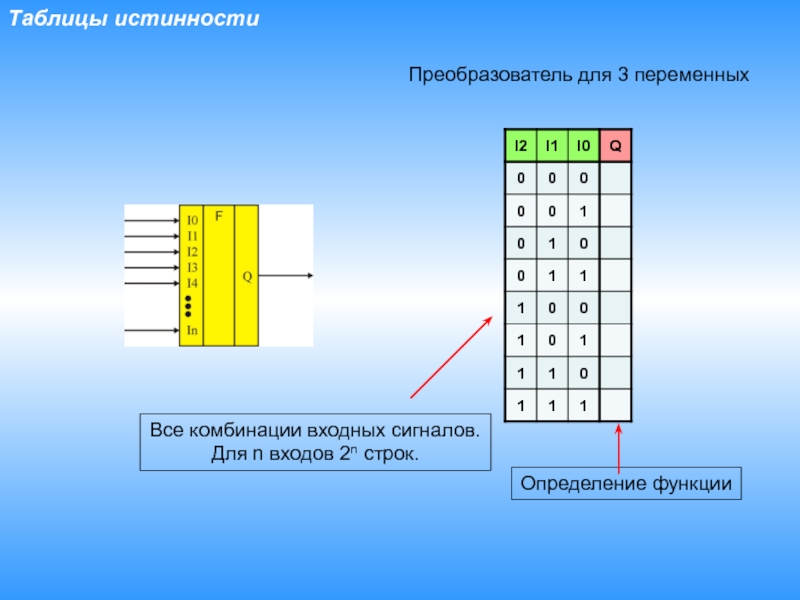
- 5. Таблицы истинностиВсе комбинации входных сигналов.Для n входов 2n строк.Определение функцииПреобразователь для 3 переменных
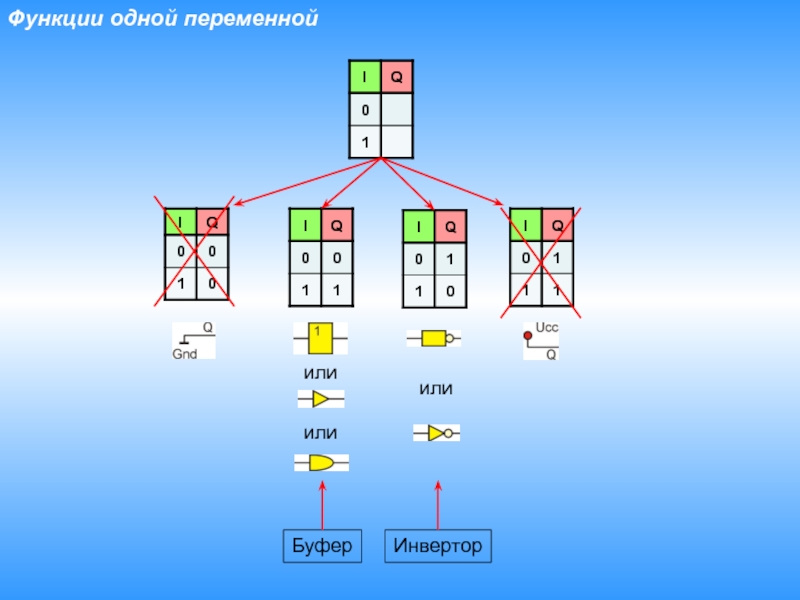
- 6. Функции одной переменнойилиБуферИнверторилиили
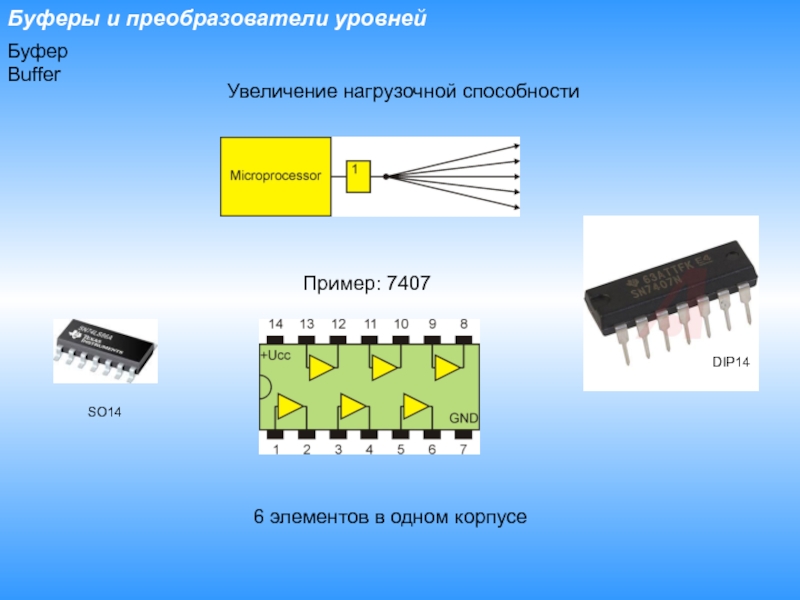
- 7. Буферы и преобразователи уровнейБуферBufferУвеличение нагрузочной способностиПример: 74076 элементов в одном корпусеDIP14SO14
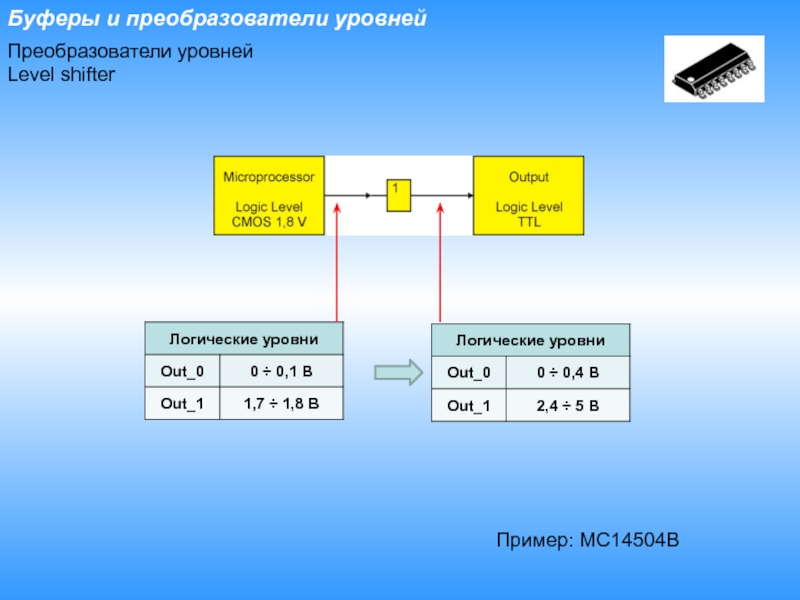
- 8. Буферы и преобразователи уровнейПреобразователи уровнейLevel shifterПример: MC14504B
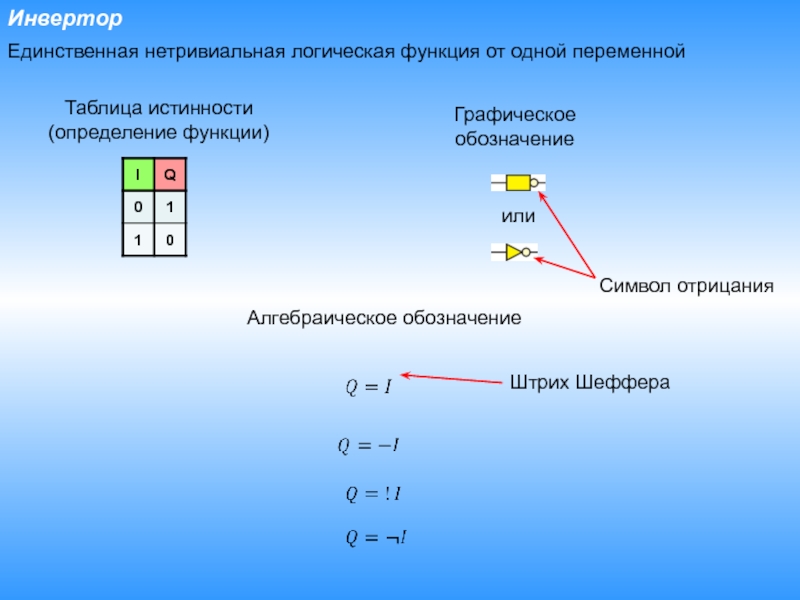
- 9. ИнверторЕдинственная нетривиальная логическая функция от одной переменнойилиТаблица истинности (определение функции)Графическое обозначениеСимвол отрицания Алгебраическое обозначениеШтрих Шеффера
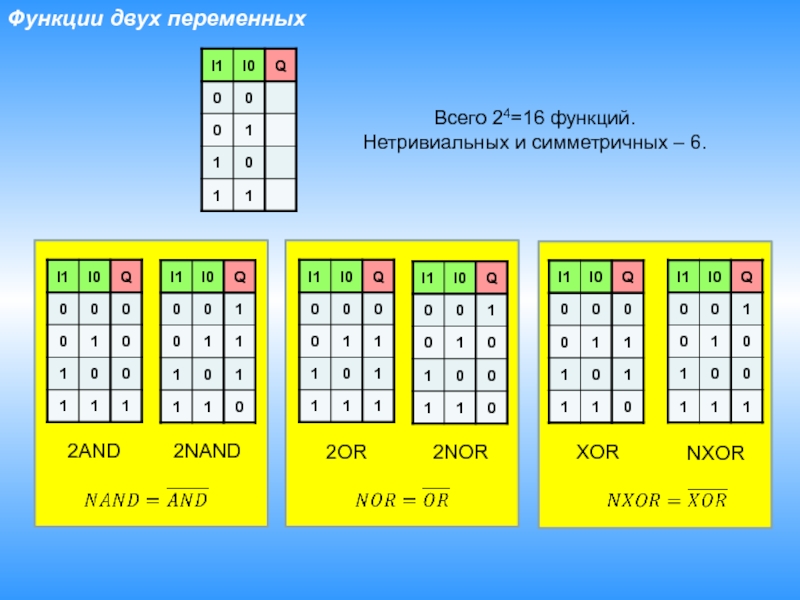
- 10. Функции двух переменныхВсего 24=16 функций.Нетривиальных и симметричных – 6.2AND2NAND2OR2NORXORNXOR
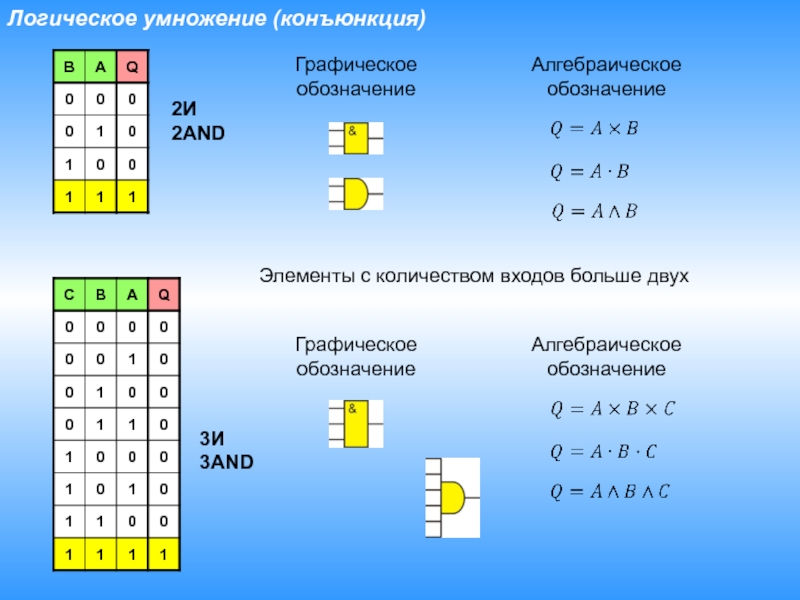
- 11. Логическое умножение (конъюнкция)ГрафическоеобозначениеАлгебраическоеобозначение Элементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение 2И2AND3И3AND
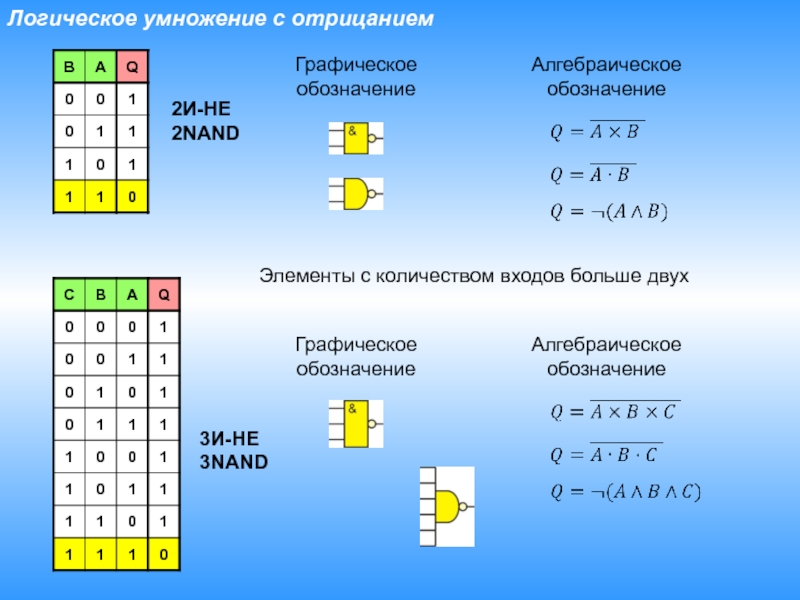
- 12. Логическое умножение с отрицаниемГрафическоеобозначениеАлгебраическоеобозначение Элементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение 2И-НЕ2NAND3И-НЕ3NAND
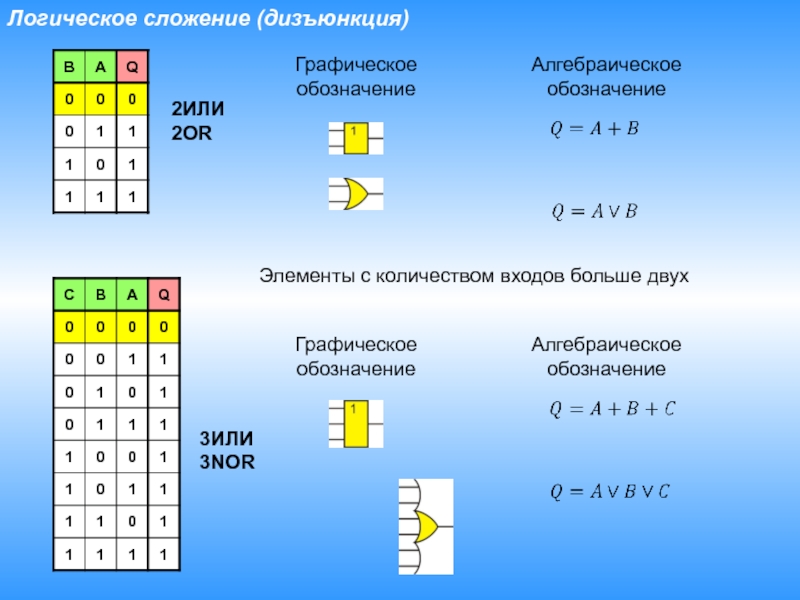
- 13. Логическое сложение (дизъюнкция)ГрафическоеобозначениеАлгебраическоеобозначение Элементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение 2ИЛИ2OR3ИЛИ3NOR
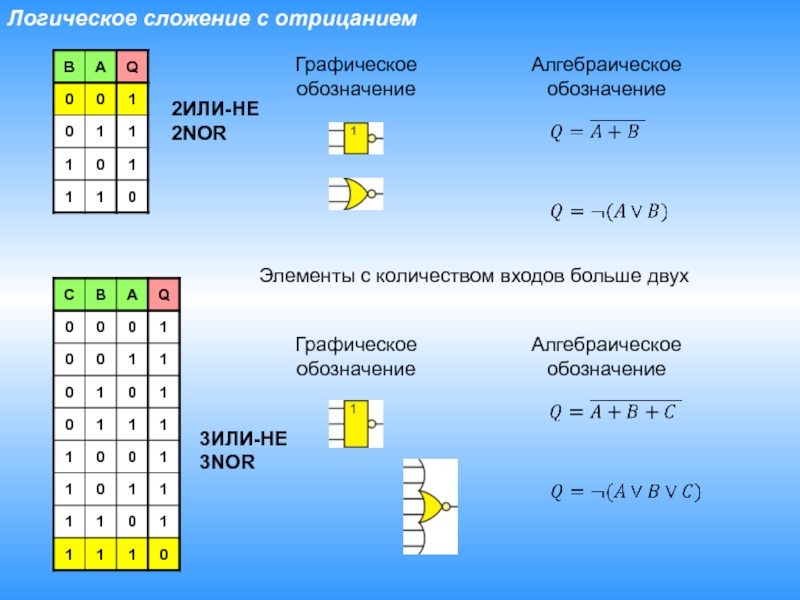
- 14. Логическое сложение с отрицаниемГрафическоеобозначениеАлгебраическоеобозначение Элементы с количеством входов больше двухГрафическоеобозначениеАлгебраическоеобозначение 2ИЛИ-НЕ2NOR3ИЛИ-НЕ3NOR
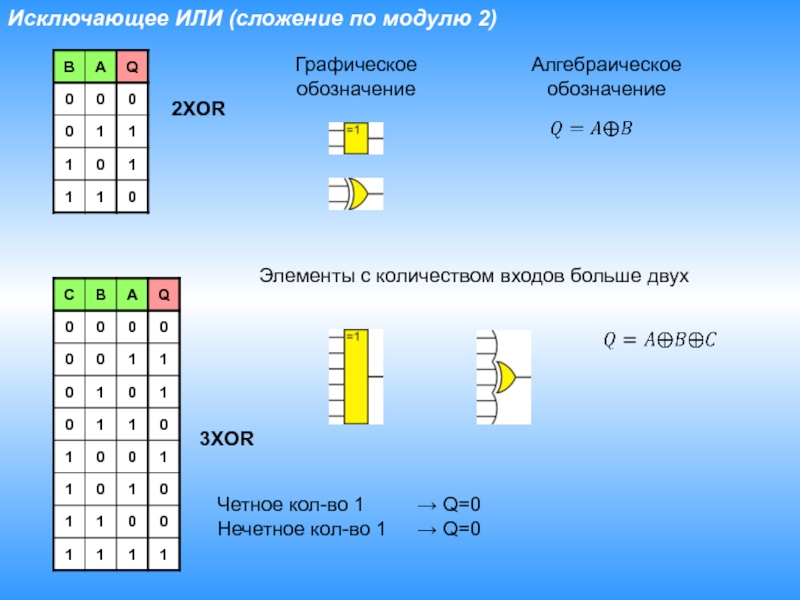
- 15. Исключающее ИЛИ (сложение по модулю 2)ГрафическоеобозначениеАлгебраическоеобозначение Элементы с
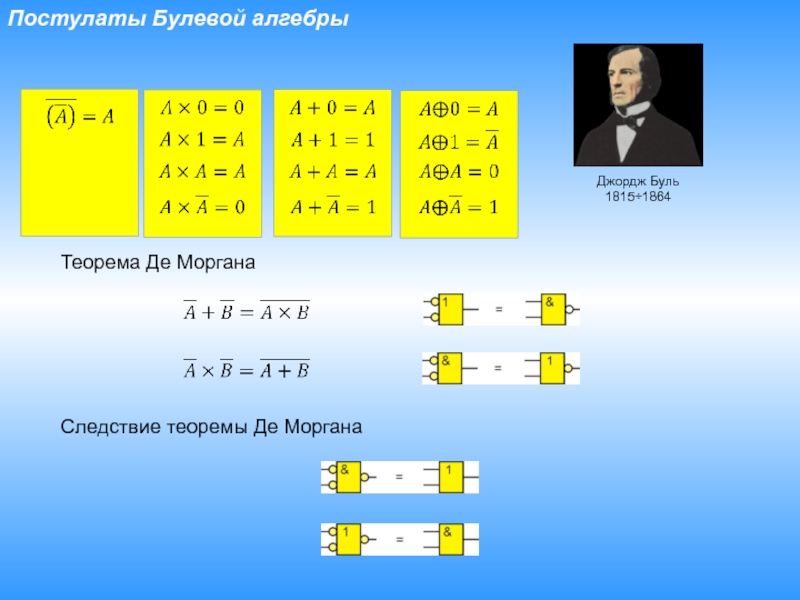
- 16. Постулаты Булевой алгебры Теорема Де Моргана Следствие теоремы Де МорганаДжордж Буль1815÷1864
- 17. Законы Булевой алгебрыКоммутативный Дистрибутивный Ассоциативный
- 18. Скачать презентанцию
ЛогикаЛОГИКАКомбинаторнаяПоследовательностнаяПреобразование кодовЛогика с памятью