Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
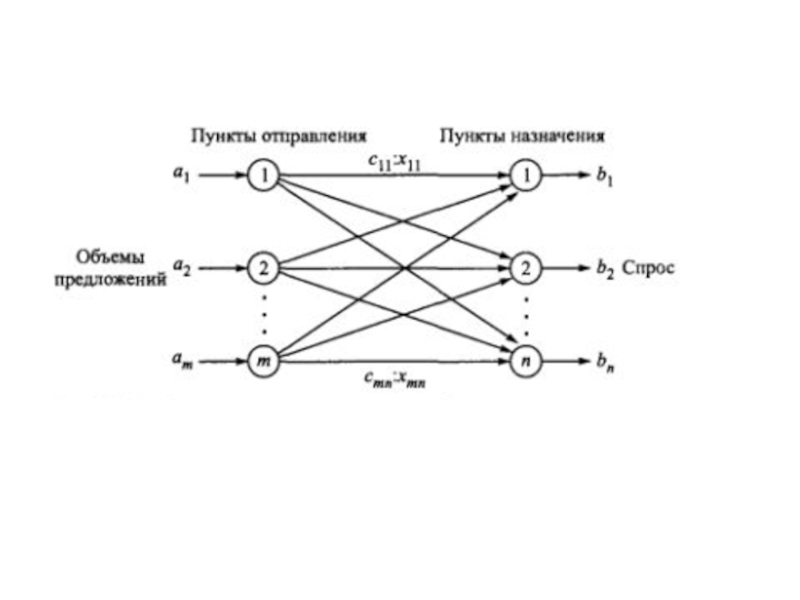
Введение в управление запасами
Содержание
- 1. Введение в управление запасами
- 2. хранение 5 тыс $90 тыс $90 тыс $потомсразуn лет
- 3. решить задачу управления запасами процент 0,01(2b+d) 1/год,
- 4. СтоимостьтранзакцииЦена храненияВеличина расходаЗадача оценитьБ) объём денежной массы в странеА) индив. Спрос на деньги.
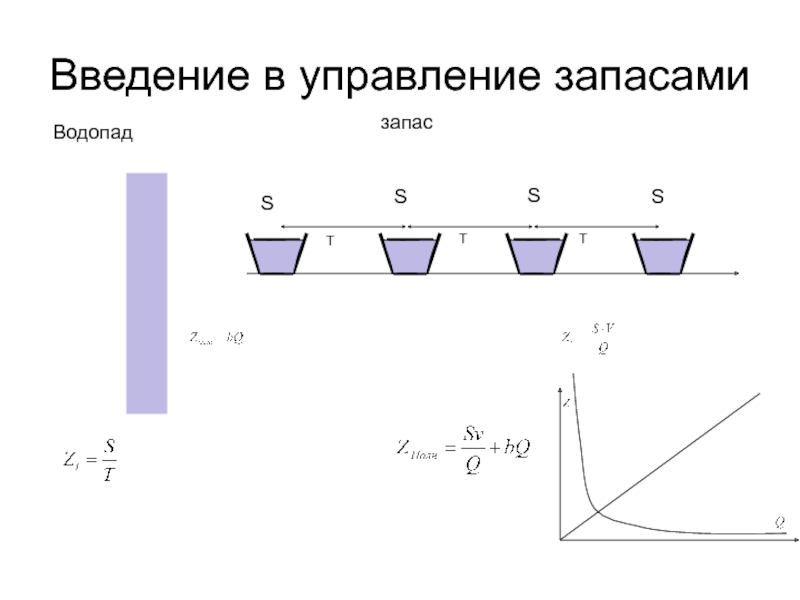
- 5. Введение в управление запасами ВодопадзапасSSSSОптимальный размер заказаTTTZQ
- 6. СтоимостьтранзакцииЦена храненияВеличина расходаОбъём заказа
- 7. СтоимостьтранзакцииЦена храненияВеличина расходаОбъём заказаРешить задачу управления запасами.Стоимость
- 8. Транзакционные издержки
- 9. TTTTSSSSSQQQV, bГрафик: динамика запасаЕжеквартальные платежи
- 10. Введение в управление запасами ВодопадзапасSSSSTTT
- 11. Введение в управление запасами ВодопадзапасSSSSTTT
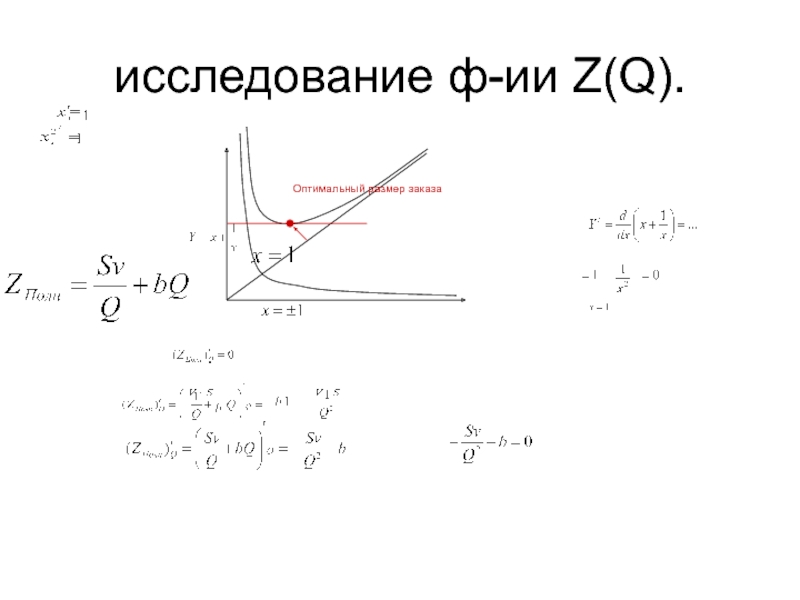
- 12. исследование ф-ии Z(Q).Оптимальный размер заказа
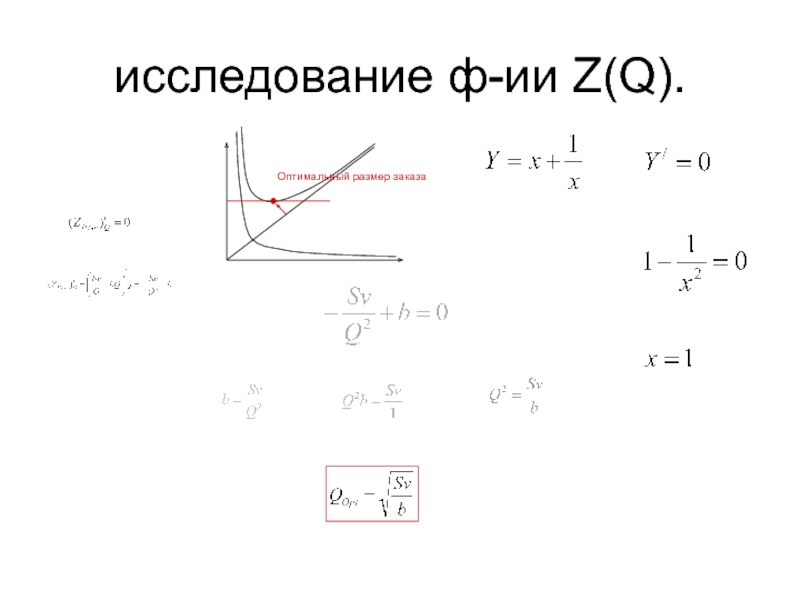
- 13. исследование ф-ии Z(Q).
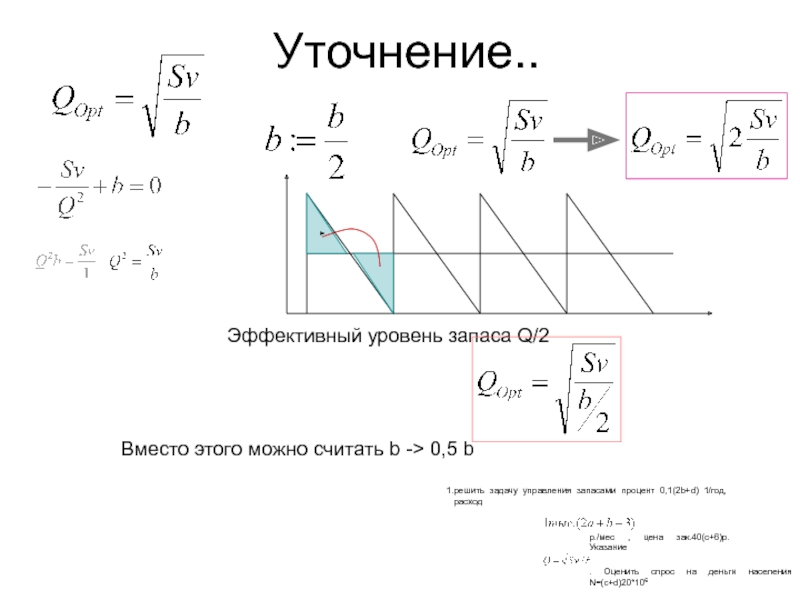
- 14. Уточнение..Эффективный уровень запаса Q/2Вместо этого можно считать
- 15. решить задачу управления запасами процент 0,14
- 16. решить задачу управления запасами процент 0,14
- 17. решить задачу управления запасами процент 0,14
- 18. решить задачу управления запасами процент 0,14
- 19. Ограничение на суммарный средний запас Ф.ЛагранжаУсловие минимумарешение2Ограничение активноОграничение НЕактивнорешение0
- 20. Жадный алгоритм Задача о построении минимального остовного дерева
- 21. Слайд 21
- 22. DH (20 км)
- 23. DH (20 км)Минимальное остовное деревоШага и ребра
- 24. 150 км34 км2500 км20 км1500 кмADHCDH (20 км)DA (34 км)
- 25. 150 км34 км2500 км20 км1500 кмADHCDH (20 км)DA (34 км)АС (1500 км)Условная оптимизация
- 26. 150 км34 км2500 км20 км1500 кмADHCDH (20
- 27. Построить мин. остовное дерево жадным алгоритмом124358.5782110113514374339201. GE
- 28. Задание и пример12-12+124358.5782110114514374339201. GE ( 1 км)
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
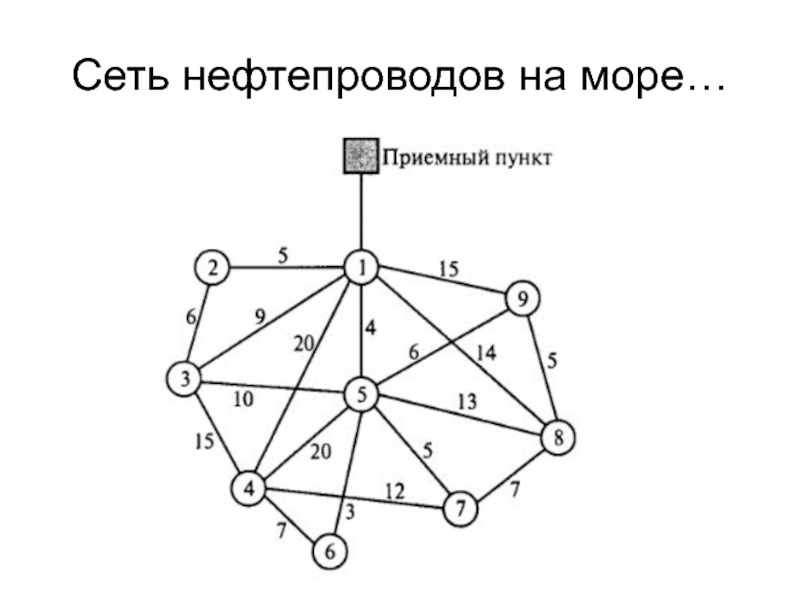
- 34. Сеть нефтепроводов на море…
- 35. Задача определения кратчайшего путиЗадача определения кратчайшего пути
- 36. кр.Пути (на неориентированном графе)склад386093809(0;-)600095503003100010111400[число,пункт] – временная метка(число,пункт)
- 37. Алгоритм Уоршаллаa100a300bcd10+d102030900800300600AA600900600600600900В1400A320C1700G50E40D910EABCDEFG320504091017001200900120032017005040910D-360=40+320D-350=30+320360FB=min(40FD+320DB;n-я итерацияn+1-я итерацияn-я итерацияn-я итерацияABY1Y3Y2E-960=910+50C-950=50+900E-60=10+50B-920=600+320F-960=900+40
- 38. 2Алгоритм УОРШАЛЛА125342Ищем отсутствующие рёбра22222∞∞Проверяем неравенство «Треугольника»(треугольник не фамилия)22∞∞222∞∞∞∞∞22∞∞∞222222В «2»-ку прийти нельзя33∞333ОТВЕТ:n-я итерацияn+1-я итерацияn-я итерацияn-я итерация
- 39. Кратч путьb+c(a+d+c)/3|a-b|+10c+13d+1c+d3b3d-13(d+c)+1 3d-1a+103ad+1|4-c|b+c5+aba+b+c8-a+bQBRDCEHFKLN246544615173(0, - )RBSDAF[17,S] [5,S]
- 40. Образец1325467246544615173(0, - )RBSDAF[17,S] [5,S] [6,S] (5,S)[11,A] [9,A]
- 41. Самый длинный - критический - путь в графе Планирование и моделирование проекта
- 42. Слайд 42
- 43. Метод и примеры практического применения . Задача динамического программирования
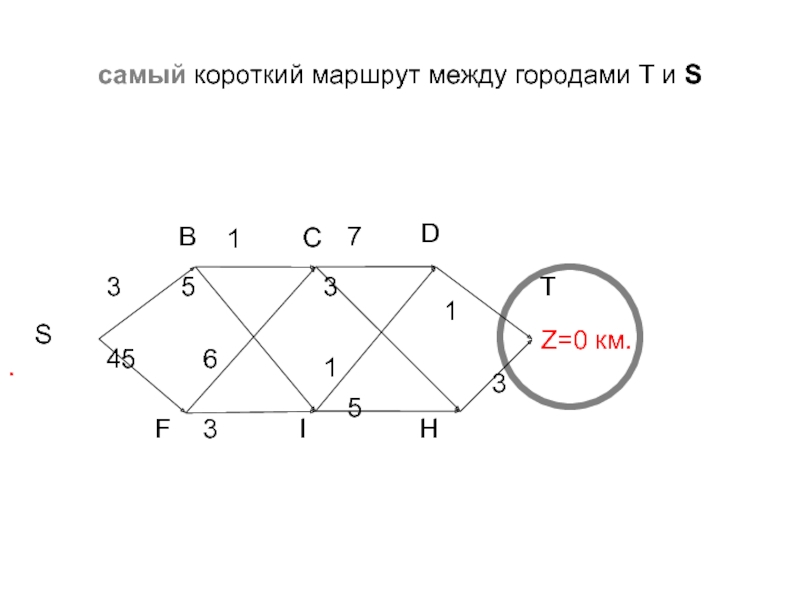
- 44. самый короткий маршрут между городами T и S 73331SBCTFI63115HZ=0 км..455D
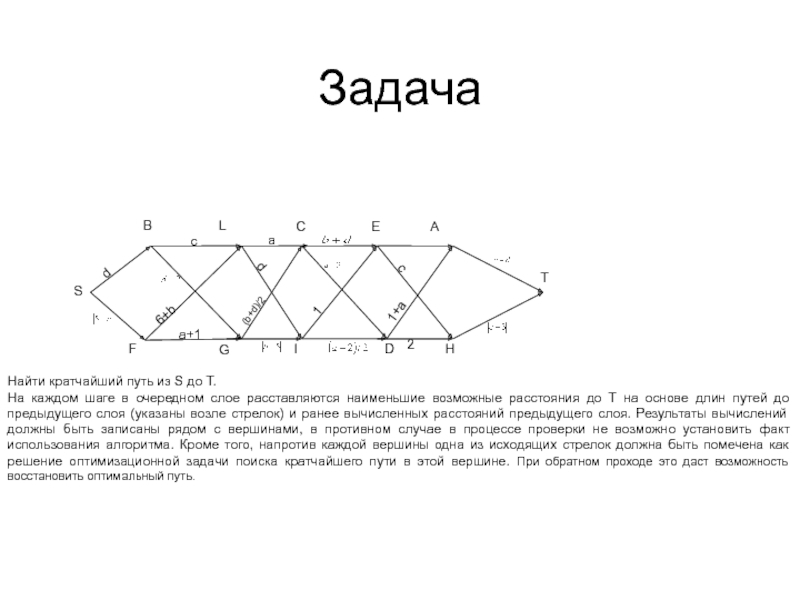
- 45. Задача
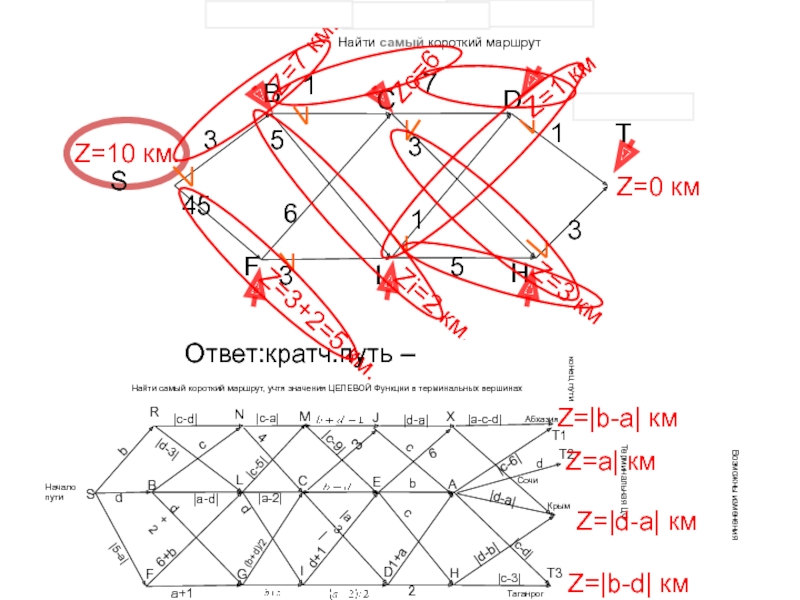
- 46. Найти самый короткий маршрут 73331SBCTFI63115HZ=0 кмZi=2 км.Z=1
- 47. Найти самый короткий маршрут 73331SBCTFI63115HZ=0 кмZi=2 км.Z=1
- 48. Найти самый короткий маршрут 73331SBCTFI63115HZ=0 кмZi=2 км.Z=1
- 49. самый короткий маршрут между городами T и S 73331SBCTFI63115HZ=0 км..Z=0+1 км.Z=0+3 км.D.455
- 50. самый короткий маршрут между городами T и
- 51. самый короткий маршрут между городами T и S 73331SBCTFI63115HZ=0 км.Zi=min(5+Zh,1+Zd)=1+1=2 км.Z=0+1 км.Z=0+3 км.Z=3+3=6DZ=2+3=5 км..Z=7 км.455
- 52. Найти самый короткий маршрут 73331SBCTFI63115HZ=0 км.Zi=min(5+Zh,1+Zd)=1+1=2 км.Z=0+1 км.Z=0+3 км.Zc=min(Zh+3,Zd+7)=3+3=6DZ=3+3=6 км.Z=10 км.Z=7 км.45Ответ:кратч.путь –…5
- 53. Найти самый короткий маршрут 73331SBCTFI63115HZ=0 км.Zi=min(5+Zh,1+Zd)=1+1=2 км.Z=0+1
- 54. Самый безопасный маршрут...Вероятность не заплатить штрафВероятность не заплатить штраф на маршруте→max→maxминус логарифмыМонотонное преобразованиеИнверсия →min
- 55. Задача планирования проекта Сетевое планирование Построение кратчайшего пути
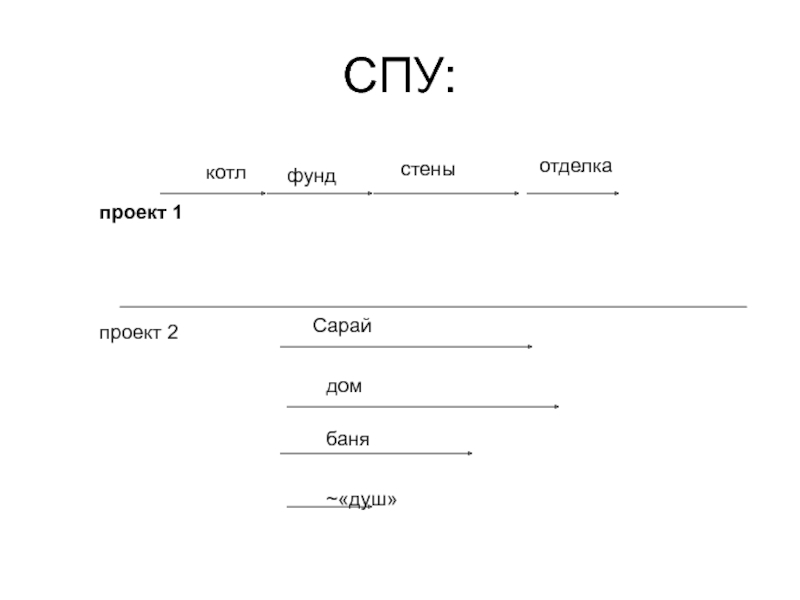
- 56. СПУ:фундстеныотделкакотлпроект 2проект 1Сарайдомбаня~«душ»
- 57. Строительство дома.ШколафундМонол(несущие) стеныКладка вн стен крышаостеклениеЧерн.отделкаПодвод коммуникацийЧистовая
- 58. Строительство дома.ШколафундМонол(несущие) стеныКладка вн стен крышаостеклениеЧерн.отделкаПодвод коммуникацийЧистовая
- 59. d|c-d||5-a||b-5|d+2|a-3||a-6|(a+2)/2b+d2
- 60. критический путьdFIHLMVCD408060301513166384354972Тр=0Ответ:Тр=40Тр=80Тр=60Тр=93Тр=109Тр=112Тр=193Тп=193Тп=177Тп=130Тп=109Тп=130-7258Тп=109-15=94Тп=109-49Тп=60Тп=0Тп=60-60Тп=193-16Строительство дома.|c-d||5-a||b-5|d+2|a-3||a-6|(a+2)/2b+d2FDCIЕго длина193 мТр=0Тр=Тр=Тр=Тр=Тр=
- 61. критический путьdFIHLMD40803015131682Тр=0Ответ:Тр=40Тр=80Тр=93Тр=95Тр=177Тп=177Тп=161Тп=161-30131Тп=109-15=80Тп=0Тп=60-60Тп=177-16Строительство дома.|c-d||5-a||b-5|d+2|a-3||a-6|(a+2)/2b+d2Его длинаТр=0Тр=Тр=Тр=Тр=Тр=S=a; R=1; D=|d-1|S=1; R=|b-a|;
- 62. критический путьFIHLMD4832168Тр=0Ответ:Тр=40Тр=80Тр=93Тр=95Тр=177Тп=177Тп=161Тп=161-30131Тп=109-15=80Тп=0Тп=60-60Тп=177-16Строительство дома.Его длинаТп=95FDMI177 месStFinТп=113Тп=96Имя«АВ»tp=10 мес.Тр=17Тр=27Тп=113Тп=9600
- 63. критический путьdFIHLMVCD408060301513166384354972Тр=0Ответ:Тр=40Тр=80Тр=60Тр=93Тр=109Тр=112Тр=193Тп=193Тп=177Тп=130Тп=109Тп=130-7258Тп=109-15=94Тп=109-49Тп=60Тп=0Тп=60-60Тп=193-16Строительство дома.|c-d||5-a||b-5|d+2|a-3||a-6|(a+2)/2b+d2FDCIЕго длина193 мТр=0Тр=Тр=Тр=Тр=Тр=S=a; R=1; D=|d-1|S=1;
- 64. ЗадачаКороткий вариантd
- 65. Обсчитанный проект из 3х работ
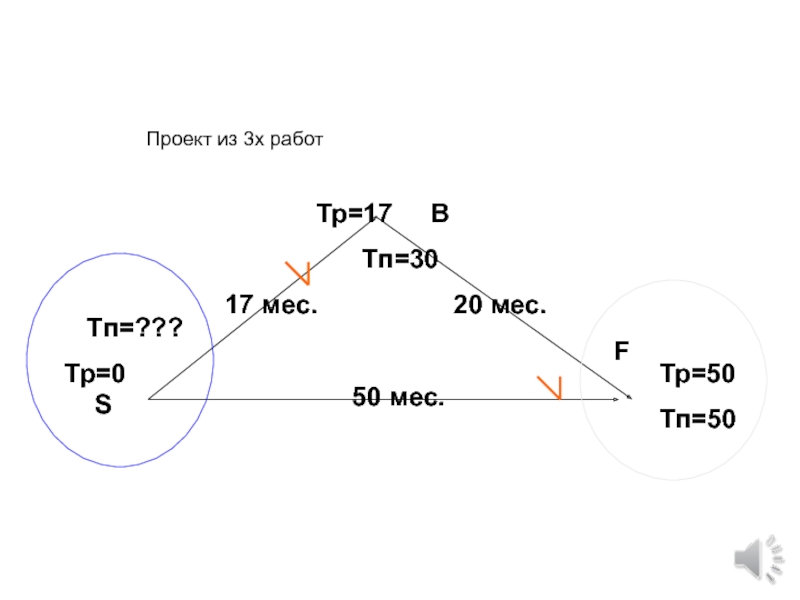
- 66. Проект из 3х работИскать не можемИщем
- 67. Проект из 3х работИщем
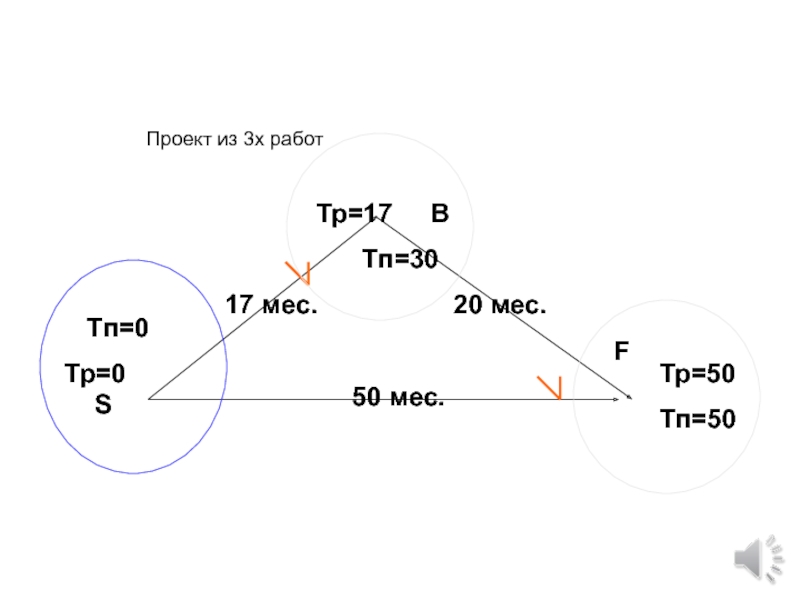
- 68. Проект из 3х работ
- 69. Проект из 3х работ
- 70. Проект из 3х работ
- 71. Проект из 3х работ
- 72. Проект из 3х работ
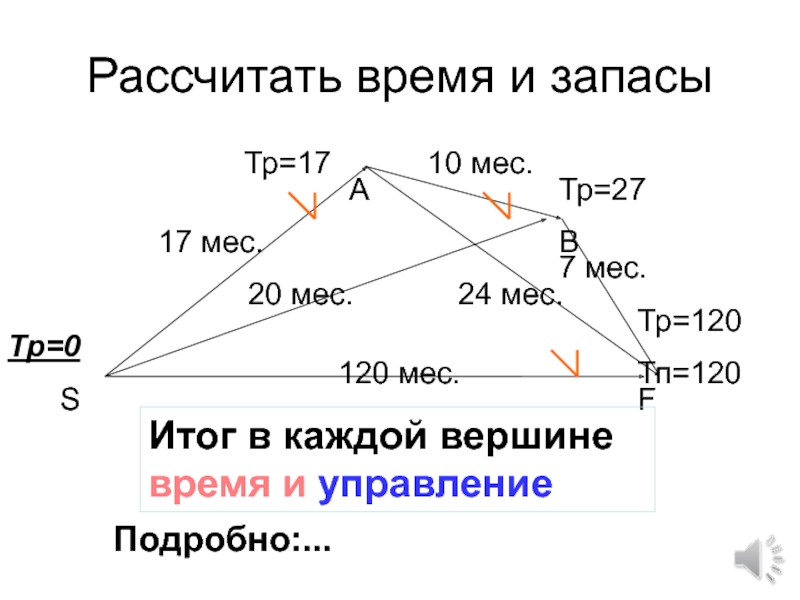
- 73. Рассчитать время и запасыИтог в каждой вершине время и управлениеПодробно:...
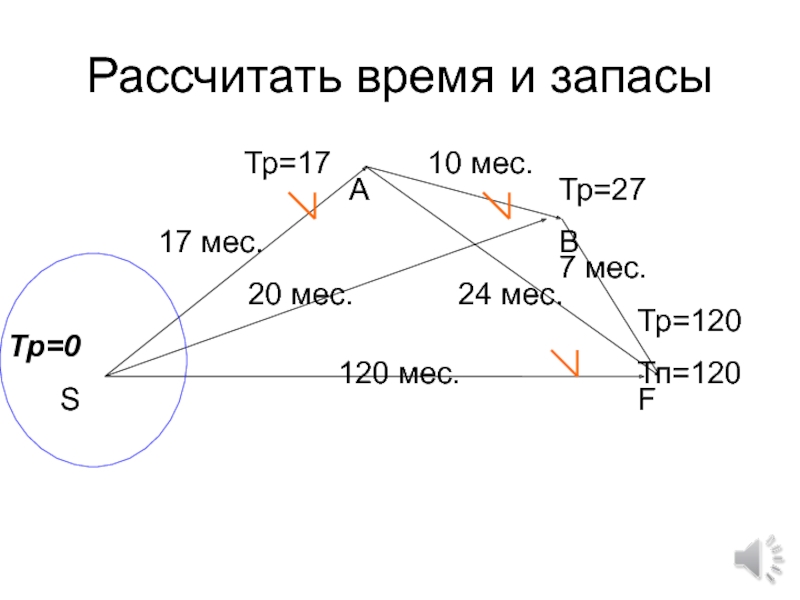
- 74. Рассчитать время и запасы
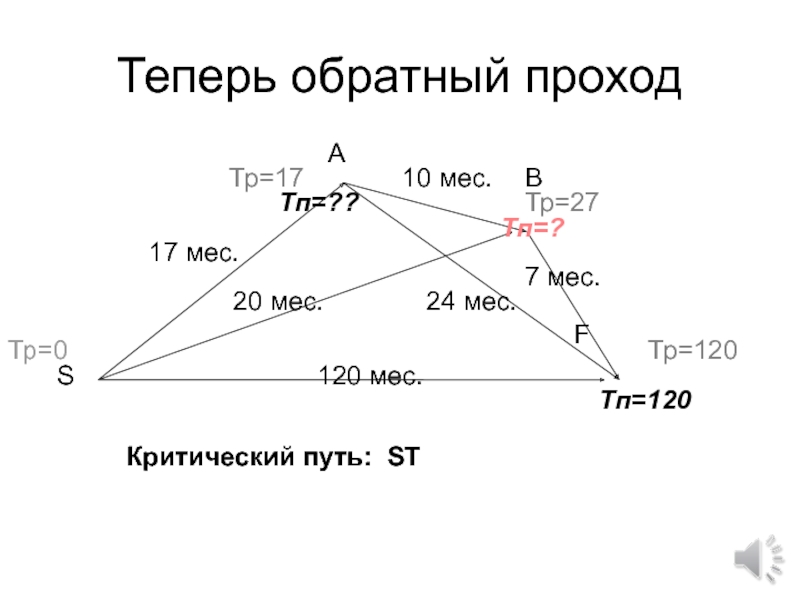
- 75. 120 мес.17 мес.20 мес.10 мес.24 мес.7 мес.Тр=0Тп=120Тр=17Тр=???ТрSFBAРассчитать время и запасы
- 76. 120 мес.17 мес.20 мес.10 мес.24 мес.7 мес.Тр=0Тп=120Тр=17Тр=27ТрSFBAРассчитать время и запасы
- 77. Рассчитать время и запасы
- 78. Теперь обратный проходКритический путь: ST
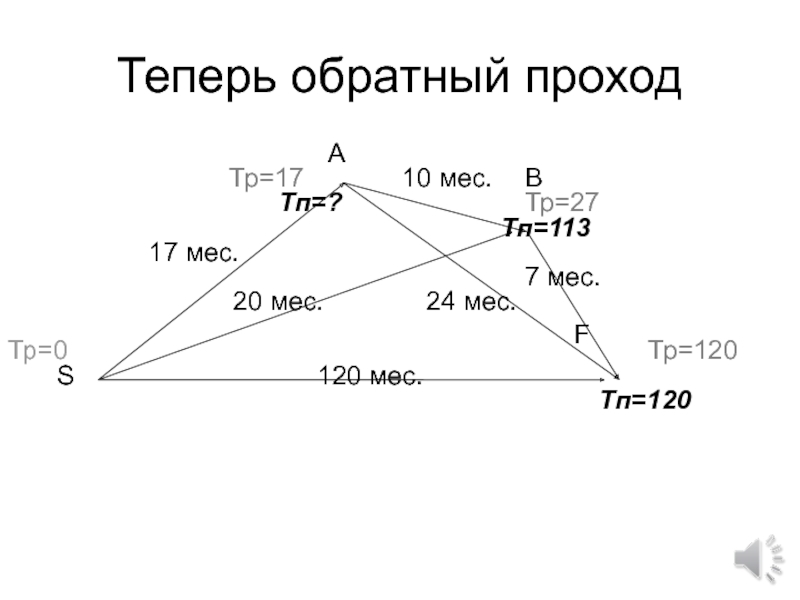
- 79. Теперь обратный проход
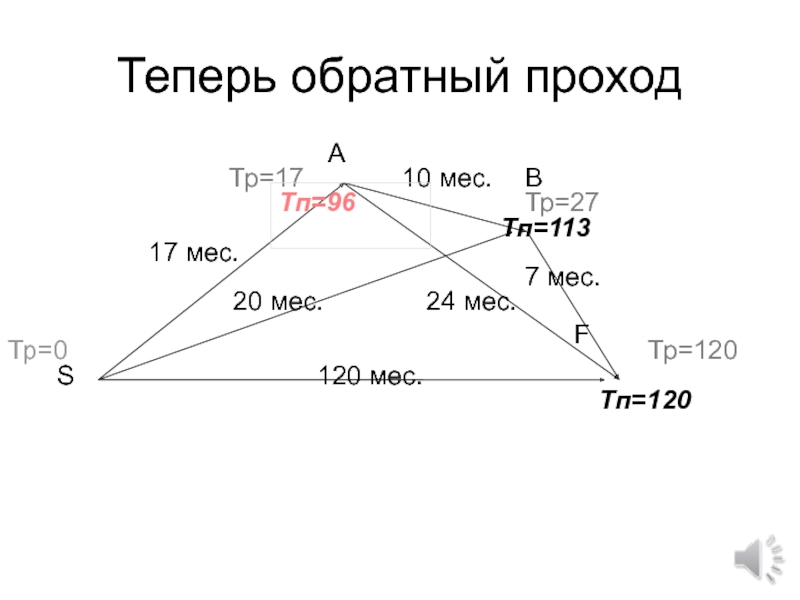
- 80. Теперь обратный проход
- 81. BATпН=96месTрН=17месTпок=113месTрок=27месRран=27-17-1010 мес.Rполн=113-17-10Rсоб=27-96-10=-79Rпоз=113-96-10На каждой работе вычислить запасы17 мес.20
- 82. TпН=96TрН=1710 мес.Tпок=113Tрок=27AB961710 мес.11327ABПо управлению проектомРассчитать ВСЕ некритические
- 83. Имя«АВ»17 мес.20 мес.10 мес.24 мес.7 мес.Тп=120Тр=17Тр=27BASТп=113Тп=96F120 мес.tp=10 мес.Тр=17Тр=27Тп=113Тп=96Имя«АВ»tp=10 мес.ТрТрТпТпSABFSFSBABAF172027120171020120724BFAFABГрафик Ганта
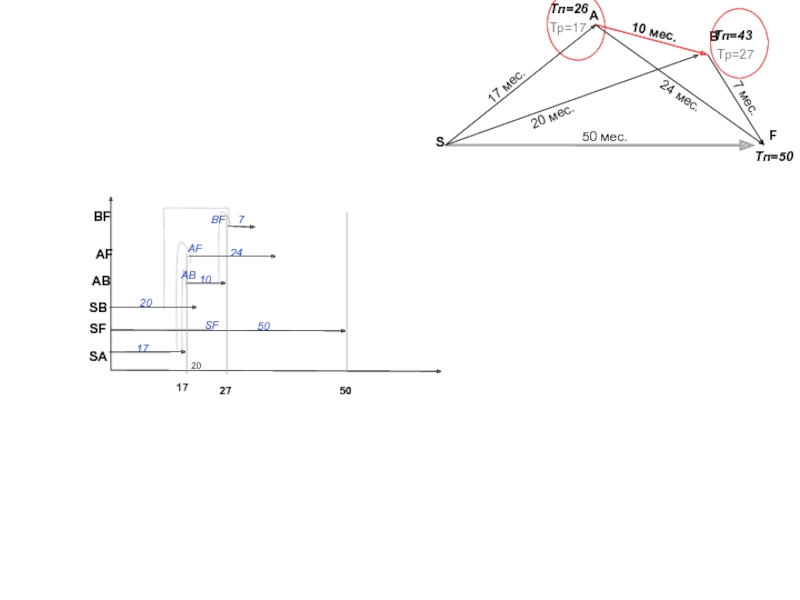
- 84. 17 мес.20 мес.10 мес.24 мес.7 мес.Тп=50Тр=17Тр=27BASТп=43Тп=26F50 мес.SABFSFSBABAF1720275017102050724BFSFABAF
- 85. Поздние времена последовательно вычисляются. Например, на первом
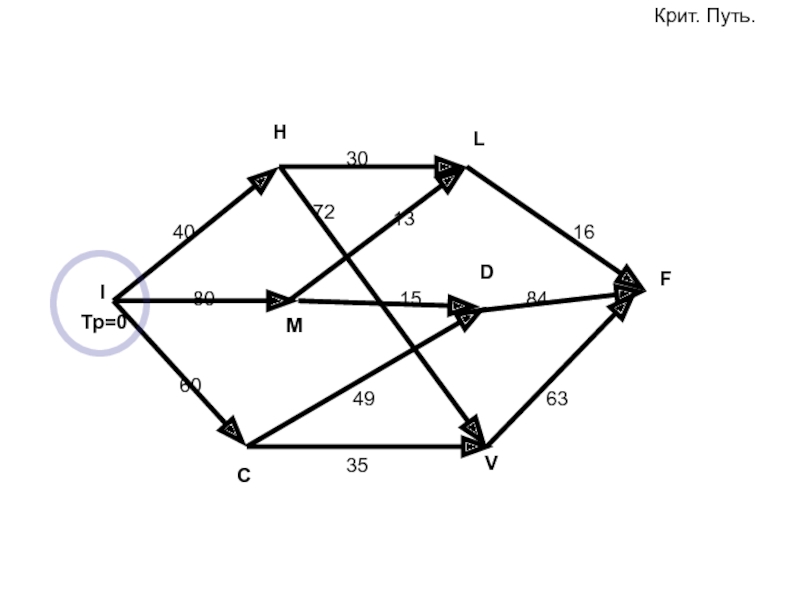
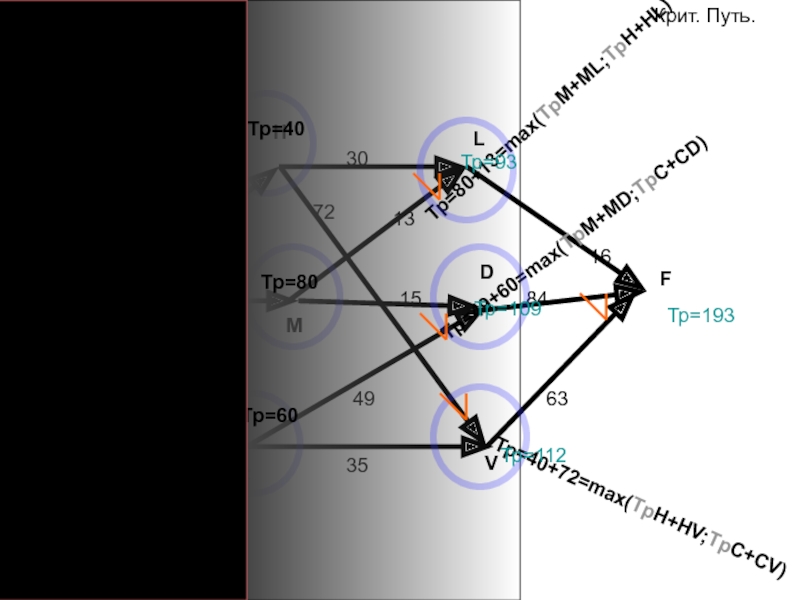
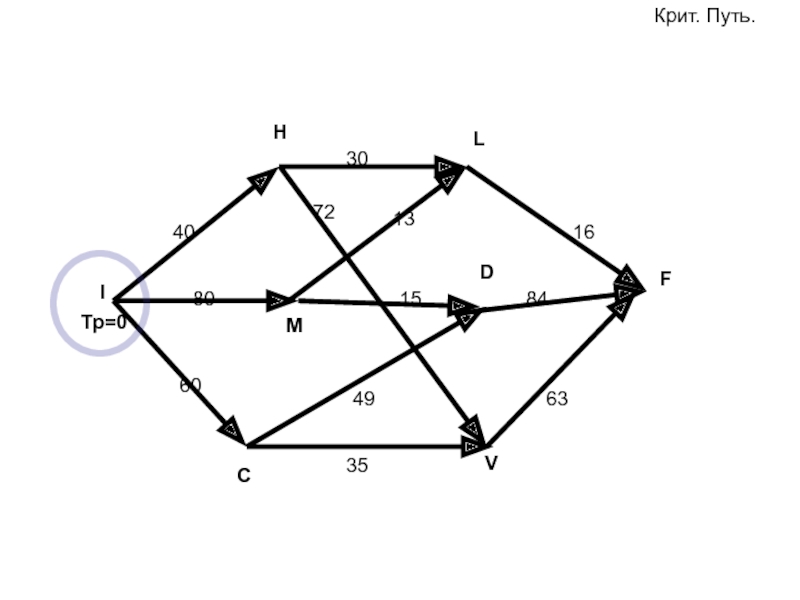
- 86. FIHLMVCD408060301513166384354972Тр=0Крит. Путь.
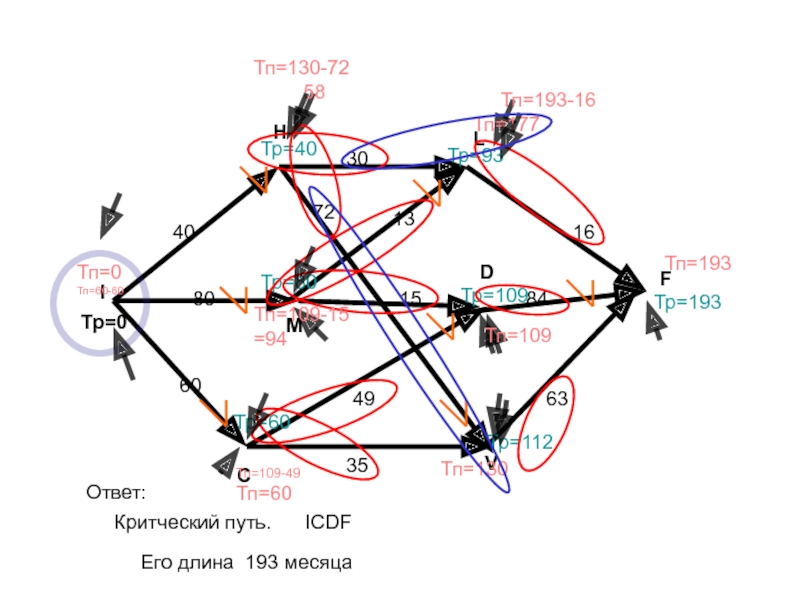
- 87. FIHLMVCD408060301513166384354972Тр=0Критческий путь.Ответ: ICDFЕго длина 193 месяца Тр=40Тр=80Тр=60Тр=93Тр=109Тр=112Тр=193Тп=193Тп=177Тп=193-16Тп=130Тп=109Тп=130-7258Тп=109-15=94Тп=109-49Тп=60Тп=0Тп=60-60
- 88. Замена оборудованияУст. Оборудование теряет в стоимости:1й год
- 89. Замена оборудования Оборудование стоит 4000 р.Уст. Оборудование
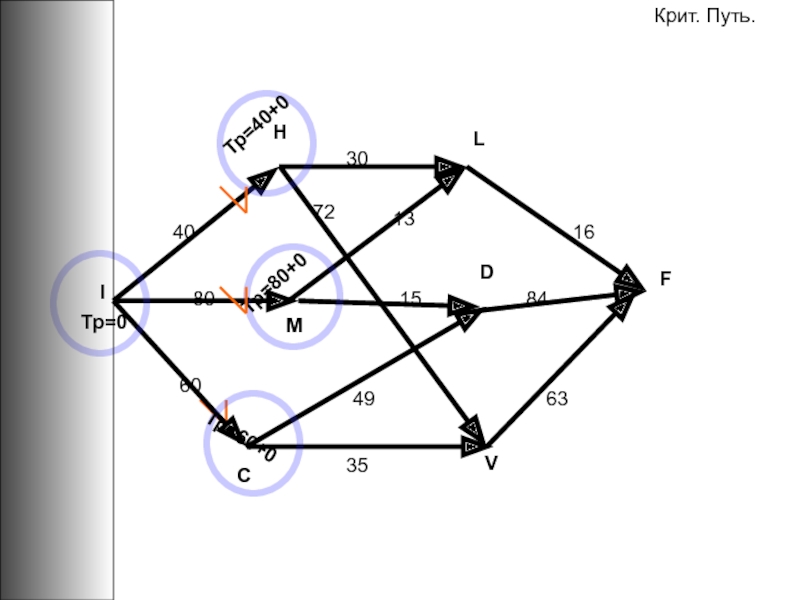
- 90. FIHLMVCD408060301513166384354972Тр=0Крит. Путь.Тр=40+0Тр=80+0Тр=60+0
- 91. FIHLMVCD408060301513166384354972Тр=0Крит. Путь.Тр=40Тр=80Тр=60Тр=80+13=max(TpM+ML;TpH+HL)Тр=49+60=max(TpM+MD;TpC+CD)Тр=40+72=max(TpH+HV;TpC+CV)Тр=93Тр=109Тр=112Тр=193
- 92. FIHLMVCD408060301513166384354972Тр=0Крит. Путь.Тр=40+0Тр=80+0Тр=60+0Тр=93=max(TpM+ML;TpH+HL)Тр=109=max(TpM+MD;TpC+CD)Тр=40+72=max(TpH+HV;TpC+CV)Тр=109+84=193==max(TpL+LF;TpD+DF;TpV+VF)Тр=193
- 93. FIHLMVCD408060301513166384354972Тр=0Крит. Путь.
- 94. Вероятностное дин. программирование
- 95. Решение:
- 96. Пример: Забега вперёд
- 97. Слайд 97
- 98. Слайд 98
- 99. Слайд 99
- 100. ответ
- 101. симплекс и граф. методы. Задача управления ресурсами, двойственная задача...
- 102. метод потенциалов транспортная задача Метод минимального элемента , Метод Северо-западного угла и
- 103. Условие: . решение:Исходное решение построить методом минимального
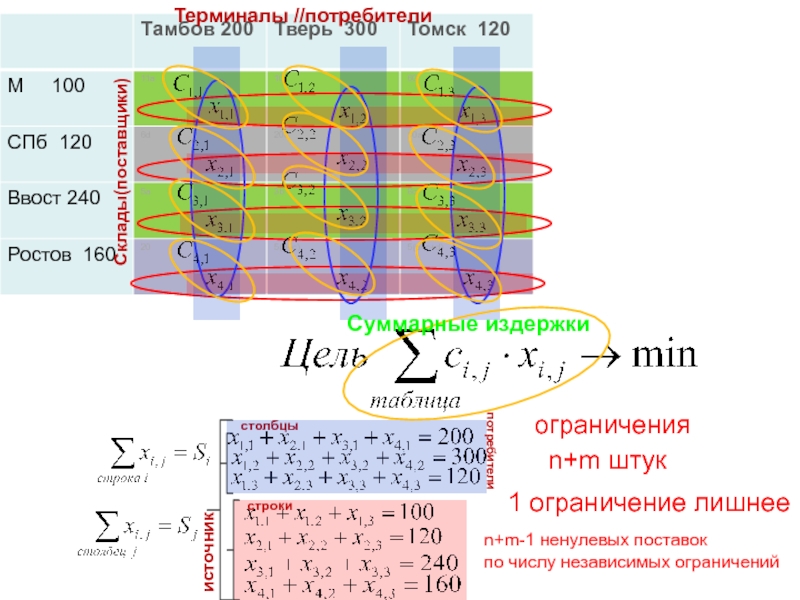
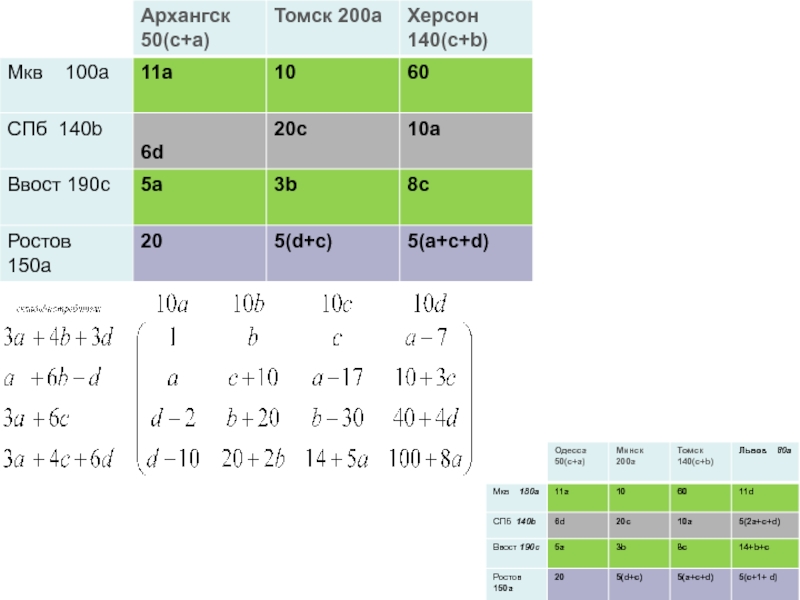
- 104. столбцыстрокиСклады(поставщики)Терминалы //потребителиСуммарные издержкиисточникпотребителистокограниченияn+m штукn+m-1 ненулевых поставок по числу независимых ограничений 1 ограничение лишнее
- 105. Слайд 105
- 106. Слайд 106
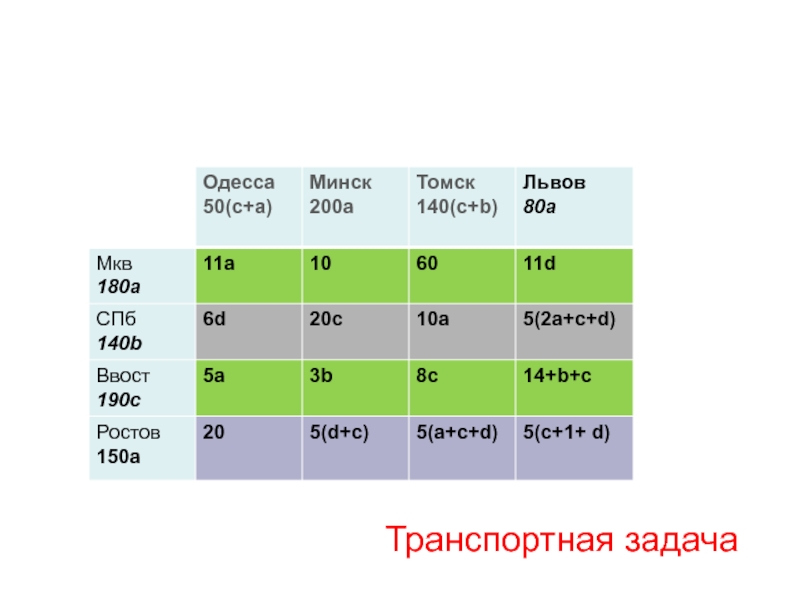
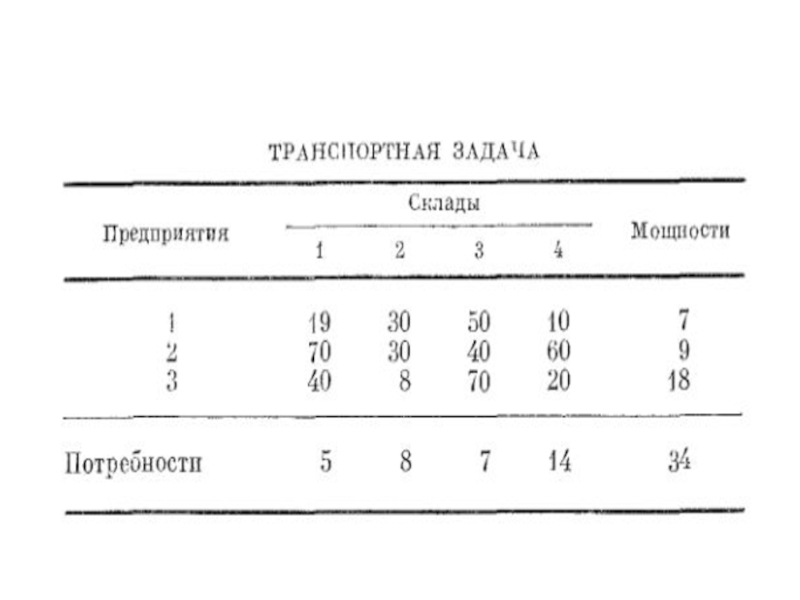
- 107. Транспортная задача
- 108. Транспортная задачаМin(100,200)=100Мin(120,100)=100Мin(20,300)=20Мin(240,280)=240Мin(160,40)= 40Мin(120,120)=120Метод Северо-Западного Угла(0)(0)(0)(0)(0)(0)(0)
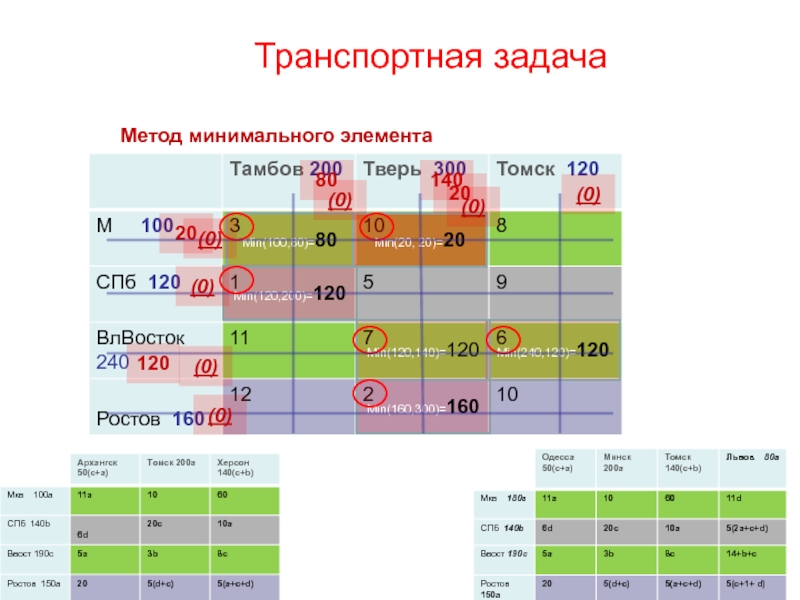
- 109. Транспортная задачаМin(120,200)=120Мin(160,300)=160Мin(100,80)=80Мin(240,120)=120Мin(120,140)=120Мin(20, 20)=20Метод минимального элемента801402012020(0)(0)(0)(0)(0)(0)(0)
- 110. Транспортная задачаx21= 120x42= 160x11=80x33= 120x32= 120x12= 20Метод ПотенциаловтаможняВывозные пошлиныВвозные пошлиныНовые тарифы
- 111. Транспортная задачаx21= 120 .x42= 160x11=80x33=
- 112. 6-ти членный цикл пересчёта
- 113. «Теорема». Для каждой базисной переменной существует ровно
- 114. Транспортная задачаx21= 100 x42= 160x11=100x33= 120x32= 120x22=
- 115. Склады(поставщики)Терминалы //потребителиСуммарные издержки
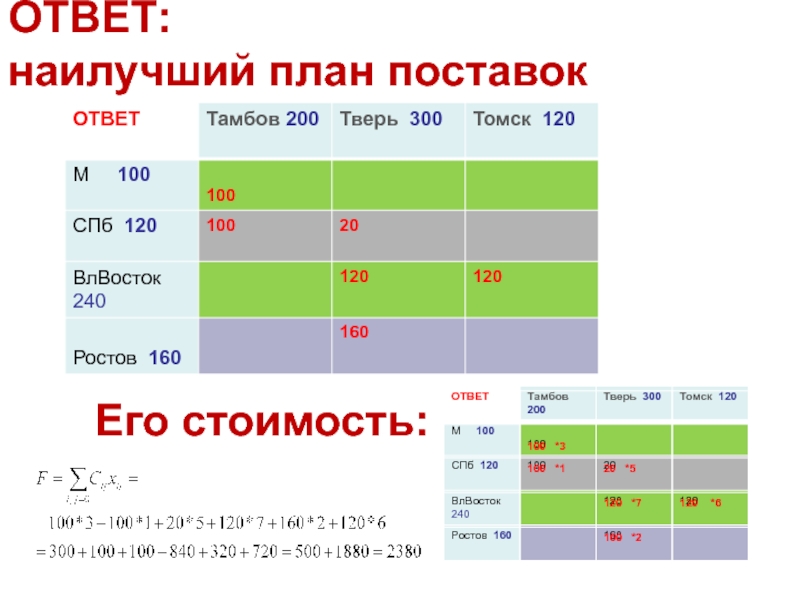
- 116. ОТВЕТ: наилучший план поставокЕго стоимость:
- 117. Слайд 117
- 118. Операционная стоимость
- 119. БАЗИСНЫЙ ПЛАН: значение ЦФ/ Лучше возможно?!
- 120. БАЗИСНЫЙ ПЛАН: значение ЦФ/ Лучше возможно?!Выбираем небазисную переменнуюУменьшаем целевую функцию до бесконечности?
- 121. Лучше возможно?!: Двойственная задача и метод потенциаловВыбираем небазисную переменнуюУменьшаем целевую функцию до бесконечности?
- 122. Уменьшаем целевую функцию до бесконечности?Т.к. уменьшающиеся поставки должны остаться положительными
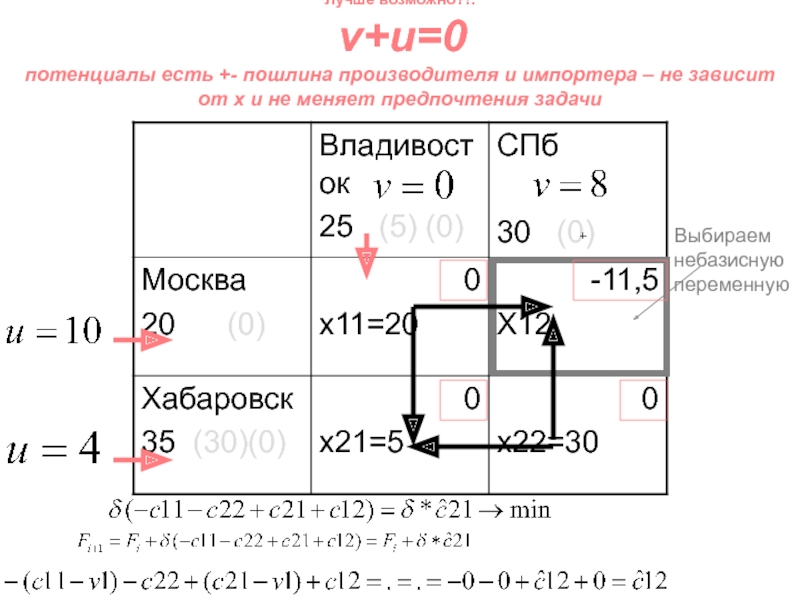
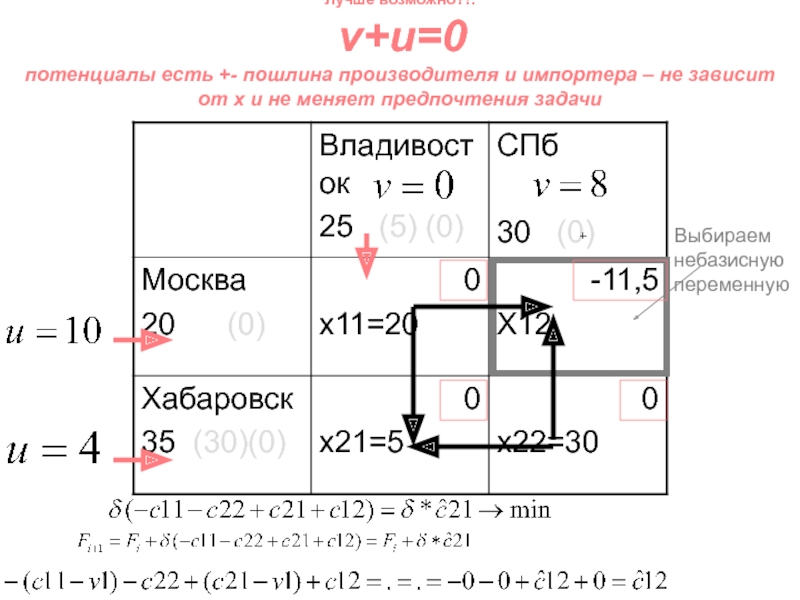
- 123. Лучше возможно?!: v+u=0 потенциалы
- 124. Лучше возможно?!: Двойственная задача и метод потенциаловВыбираем небазисную переменную
- 125. Лучше возможно?!: Двойственная задача и метод потенциаловВыбираем небазисную переменную
- 126. Лучше возможно?!: Двойственная задача и метод потенциаловВыбираем небазисную переменную
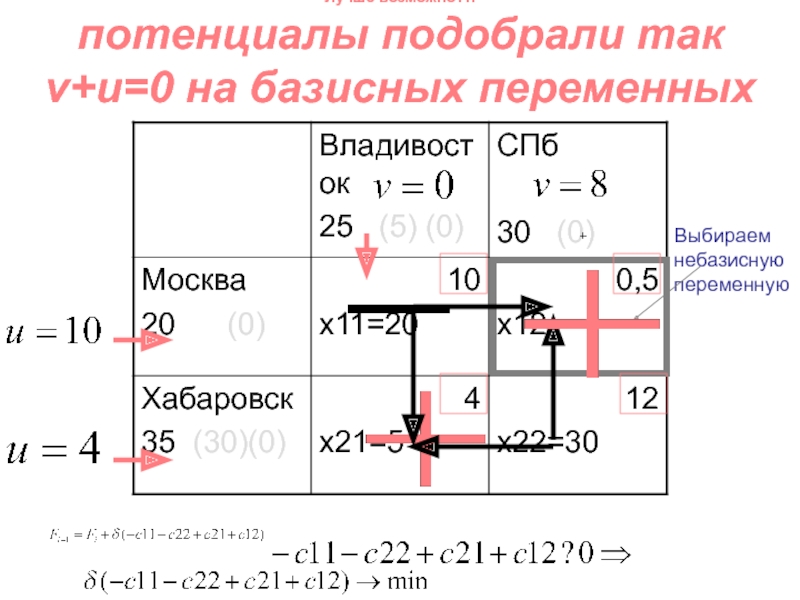
- 127. Лучше возможно?!: потенциалы подобрали так v+u=0 на базисных переменныхВыбираем небазисную переменную
- 128. Лучше возможно?!: v+u=0 потенциалы
- 129. Лучше возможно?!: v+u=0 потенциалы
- 130. Слайд 130
- 131. Слайд 131
- 132. Слайд 132
- 133. Слайд 133
- 134. Слайд 134
- 135. БАЗИСНЫЙ ПЛАН ПОСТРОЕН!!!
- 136. Слайд 136
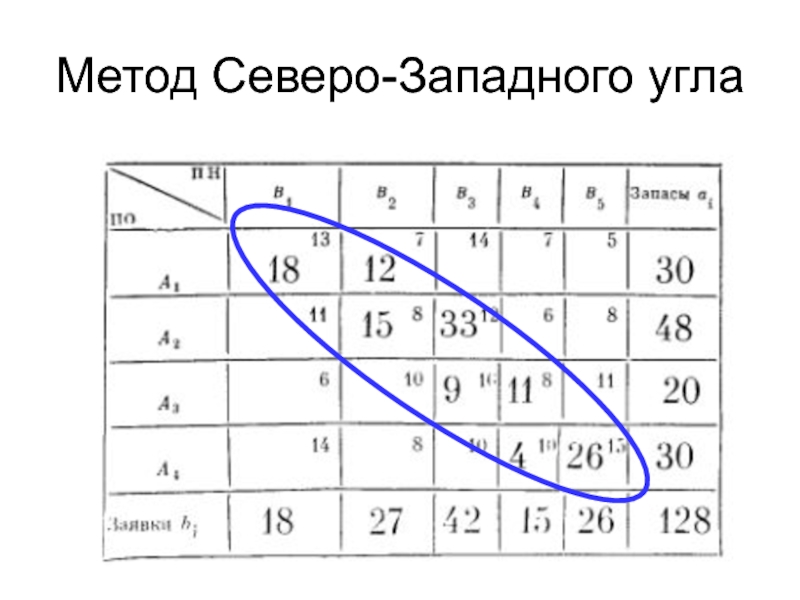
- 137. Метод Северо-Западного угла
- 138. Слайд 138
- 139. Слайд 139
- 140. Переход по циклу
- 141. Слайд 141
- 142. Слайд 142
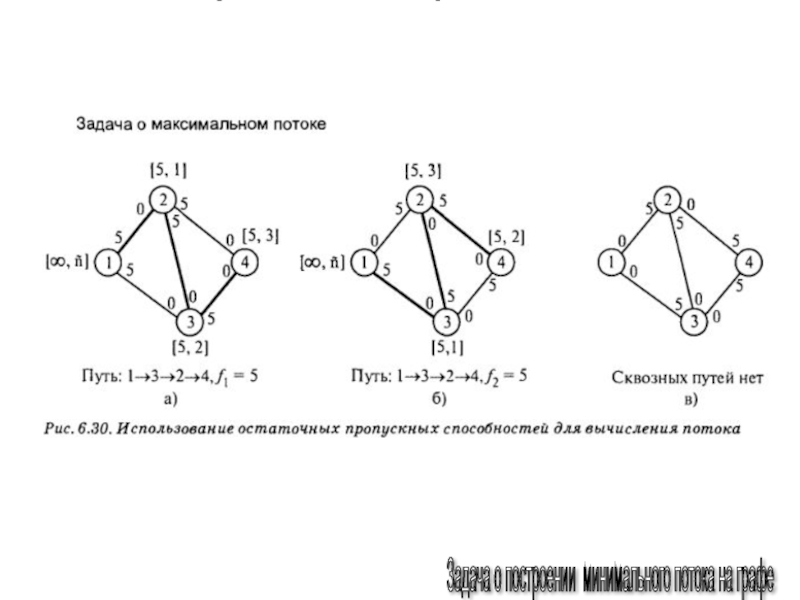
- 143. Алгоритм Форда Задача о построении минимального потока на графе
- 144. Алгоритм Дейкстры Задача о построении минимального потока на графе
- 145. Слайд 145
- 146. Алгоритм Дейкстры Задача о построении минимального потока на графе
- 147. Алгоритм Форда Задача о построении минимального потока
- 148. Алгоритм Форда Задача о построении минимального потока
- 149. Алгоритм Форда Задача о построении минимального потока
- 150. Алгоритм ФОРДА Задача о построении минимального потока
- 151. Алгоритм Форда Задача о построении минимального потока
- 152. Алгоритм Дейкстры Задача о построении минимального потока
- 153. Алгоритм Форда Задача о построении минимального потока
- 154. Алгоритм Дейкстры Задача о построении минимального потока
- 155. Алгоритм Форда Задача о построении минимального потока
- 156. Алгоритм Форда Задача о построении максимального потока
- 157. Алгоритм Форда Задача о построении минимального потока
- 158. Алгоритм Дейкстры Задача о построении минимального потока
- 159. Алгоритм Форда Задача о построении минимального потока
- 160. метод потенциалов транспортная задача М-метод и
- 161. ветвей и границ или поиск с усечением Задача коммивояжёра
- 162. Слайд 162
- 163. Слайд 163
- 164. Слайд 164
- 165. Слайд 165
- 166. Стационарные маркоские цепи. Система массового обслуживания.
- 167. Система обслуживания с несколькими сервисами
- 168. Слайд 168
- 169. Формула Литтла для связи объёма и скорости обновления людей
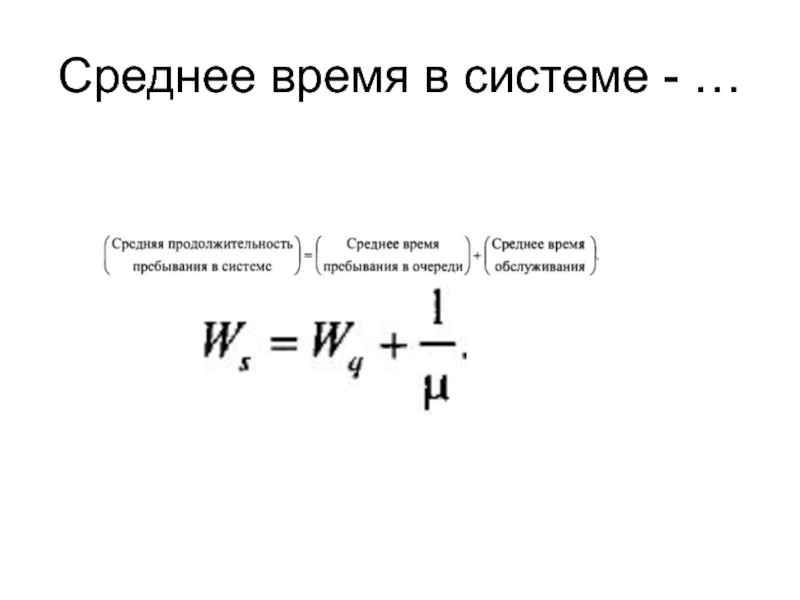
- 170. Среднее время в системе - …
- 171. критический путьFIHLMD40803015131682Тр=0Ответ:Тр=40Тр=80Тр=93Тр=95Тр=177Тп=177Тп=161Тп=161-30131Тп=109-15=80Тп=0Тп=60-60Тп=177-16Строительство дома.Его длинаТп=95FDMI177 мес
- 172. Скачать презентанцию
хранение 5 тыс $90 тыс $90 тыс $потомсразуn лет
Слайды и текст этой презентации
Слайд 3решить задачу управления запасами процент 0,01(2b+d) 1/год,
расход=
цена заказа 40(c+6)р.
Оценить
спрос на деньги населения
Слайд 4Стоимость
транзакции
Цена хранения
Величина расхода
Задача оценить
Б) объём денежной массы в стране
А) индив.
Спрос на деньги.
Слайд 7Стоимость
транзакции
Цена хранения
Величина расхода
Объём заказа
Решить задачу управления запасами.
Стоимость заказа S=a+2 тысяч
рублей,
Величина удельных издержек на хранение С=10*с руб/(шт.*день).
Величина постоянного
спроса на товар Рассчитать объем заказа(Q) при котором средние издержки на заказ и хранение минимальны (оптимальный объем заказа).
Указание: считать, что надо минимизировать функцию затрат
Слайд 14Уточнение..
Эффективный уровень запаса Q/2
Вместо этого можно считать b -> 0,5
b
решить задачу управления запасами процент 0,1(2b+d) 1/год, расход
р./мес , цена
зак.40(c+6)р. Указание. Оценить спрос на деньги населения N=(c+d)20*106
Слайд 15решить задачу управления запасами процент 0,14 1/год,
расход 20
000 р/мес.
цена заказа 180р.
решить задачу управления запасами
процент 0,01(2b+d)
1/год,расход=
цена заказа 40(c+6)р.
Оценить спрос на деньги населения
N=(c+d)20*106
р./мес ,
решить задачу управления запасами процент 0,01(2b+d) 1/год,
расход=
цена заказа 40(c+6)р.
Оценить спрос на деньги населения
N=(c+d)20*106
р./мес ,
Слайд 16решить задачу управления запасами процент 0,14 1/год,
расход 20
000 р/мес.
цена заказа 180р.
решить задачу управления запасами процент 0,01(2b+d)
1/год,расход=
цена заказа 40(c+6)р.
Оценить спрос на деньги населения
N=(c+d)20*106
р./мес ,
Слайд 17решить задачу управления запасами процент 0,14 1/год,
расход 20
000 р/мес.
цена заказа 180р.
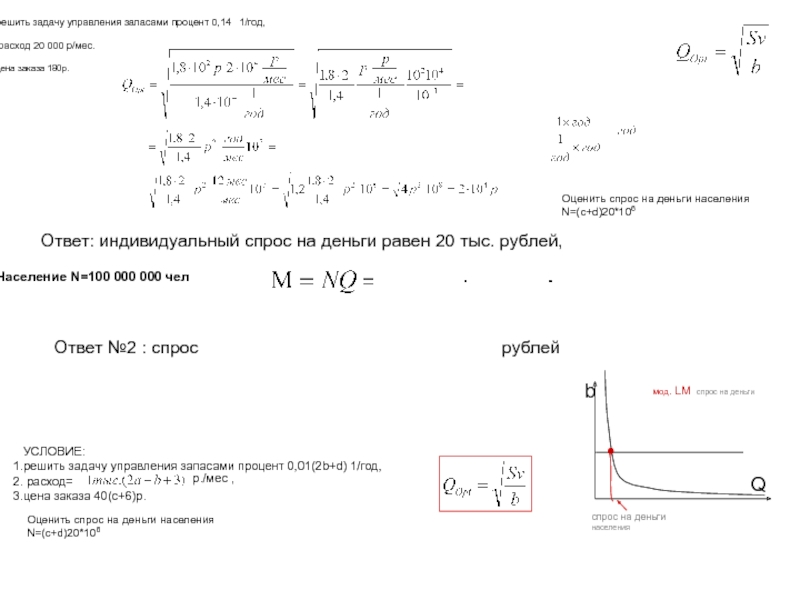
Ответ: индивидуальный спрос на деньги равен 20
тыс. рублей,УСЛОВИЕ:
решить задачу управления запасами процент 0,01(2b+d) 1/год,
расход=
цена заказа 40(c+6)р.
Оценить спрос на деньги населения
N=(c+d)20*106
р./мес ,
Слайд 18решить задачу управления запасами процент 0,14 1/год,
расход 20
000 р/мес.
цена заказа 180р.
Население N=100 000 000 чел
Ответ: индивидуальный спрос
на деньги равен 20 тыс. рублей,Ответ №2 : спрос населения на деньги равен 2 трлн. рублей
b
Q
спрос на деньги населения
УСЛОВИЕ:
решить задачу управления запасами процент 0,01(2b+d) 1/год,
расход=
цена заказа 40(c+6)р.
Оценить спрос на деньги населения
N=(c+d)20*106
р./мес ,
Оценить спрос на деньги населения
N=(c+d)20*106
Слайд 19Ограничение на суммарный средний запас
Ф.Лагранжа
Условие минимума
решение2
Ограничение активно
Ограничение НЕактивно
решение0
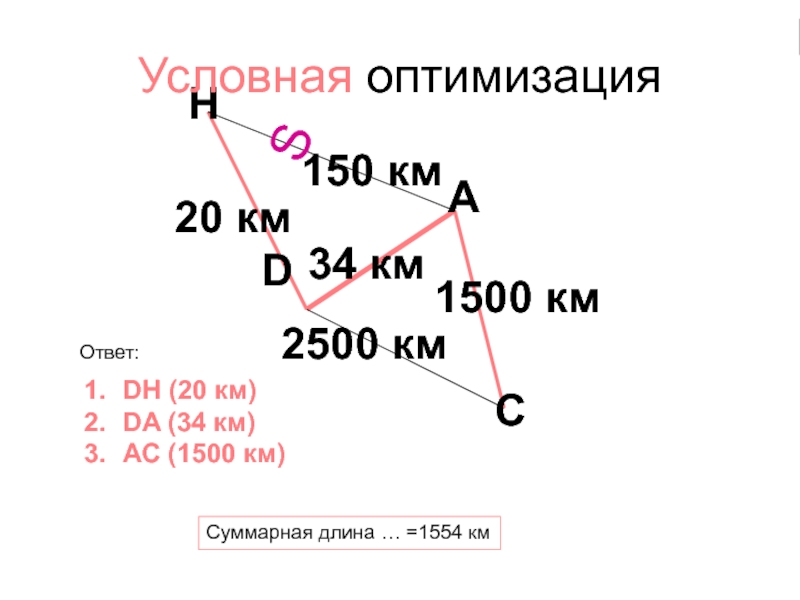
Слайд 26150 км
34 км
2500 км
20 км
1500 км
A
D
H
C
DH (20 км)
DA (34 км)
АС
(1500 км)
Условная оптимизация
Суммарная длина … =1554 км
Ответ:
S
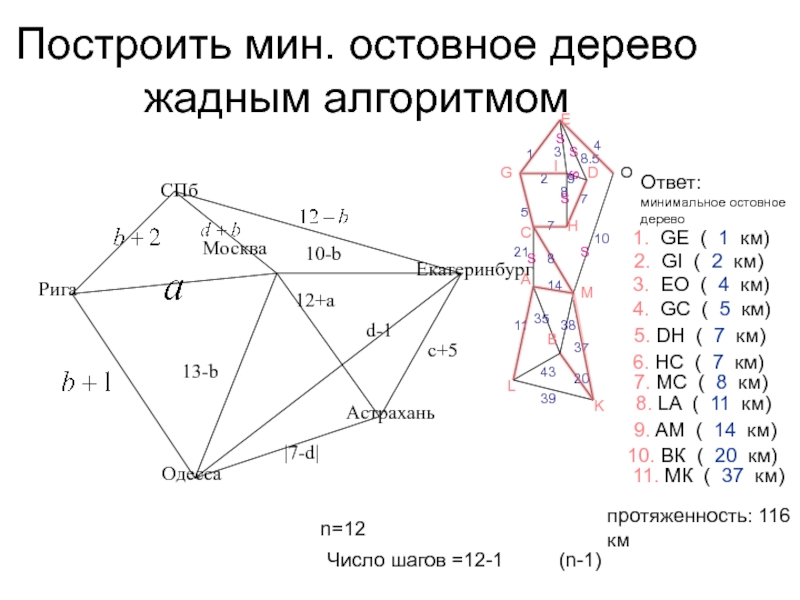
Слайд 27Построить мин. остовное дерево жадным алгоритмом
1
2
4
3
5
8.5
7
8
21
10
11
35
14
37
43
39
20
1. GE ( 1 км)
А
В
С
D
Е
Н
I
G
K
L
M
7
9
2. GI ( 2 км)
3. EO ( 4 км)
О
S
S
4. GС ( 5 км)
5. DН ( 7 км)
6. НС ( 7 км)
S
S
7. МС ( 8 км)
8
8. LA ( 11 км)
9. AM ( 14 км)
10. ВК ( 20 км)
S
38
11. МК ( 37 км)
S
Ответ:
минимальное остовное дерево
протяженность: 116 км
n=12
Число шагов =12-1 (n-1)
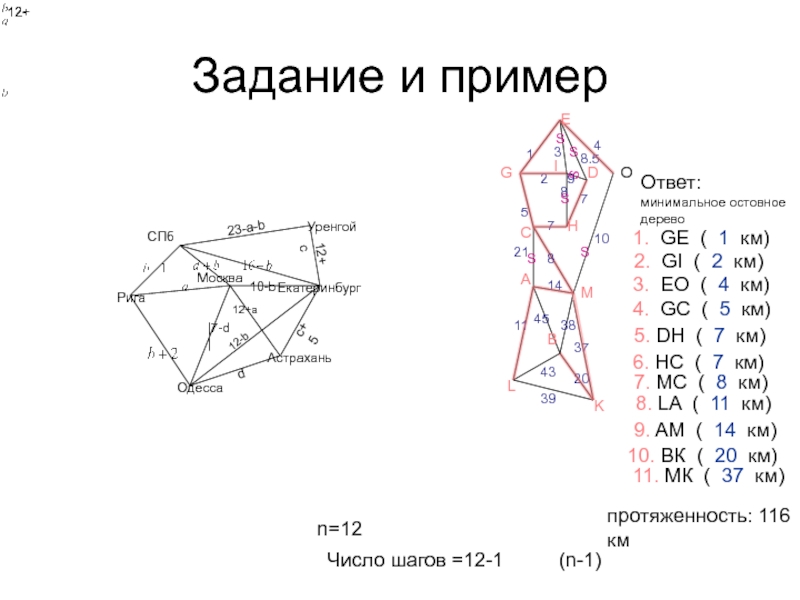
Слайд 28Задание и пример
12-
12+
1
2
4
3
5
8.5
7
8
21
10
11
45
14
37
43
39
20
1. GE ( 1 км)
А
В
С
D
Е
Н
I
G
K
L
M
7
9
2. GI (
2 км)
3. EO ( 4 км)
О
S
S
4. GС (
5 км) 5. DН ( 7 км)
6. НС ( 7 км)
S
S
7. МС ( 8 км)
8
8. LA ( 11 км)
9. AM ( 14 км)
10. ВК ( 20 км)
S
38
11. МК ( 37 км)
S
Ответ:
минимальное остовное дерево
протяженность: 116 км
n=12
Число шагов =12-1 (n-1)
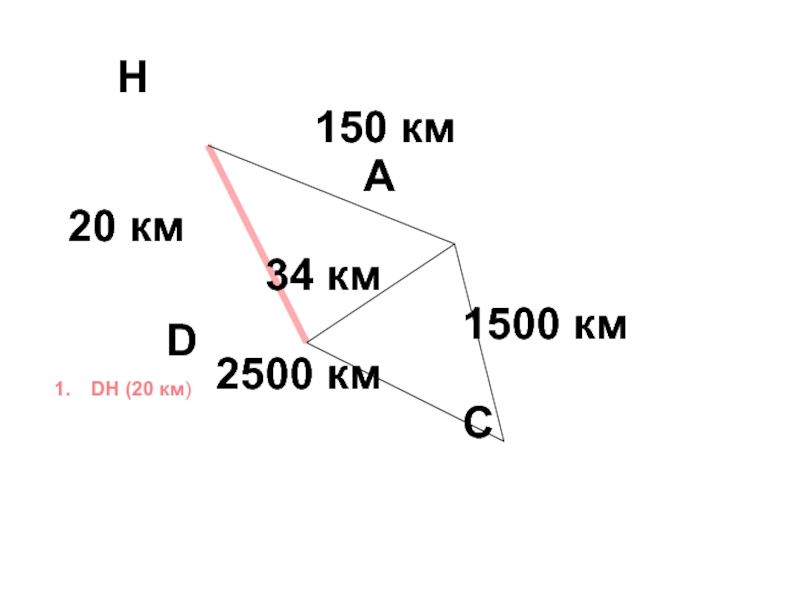
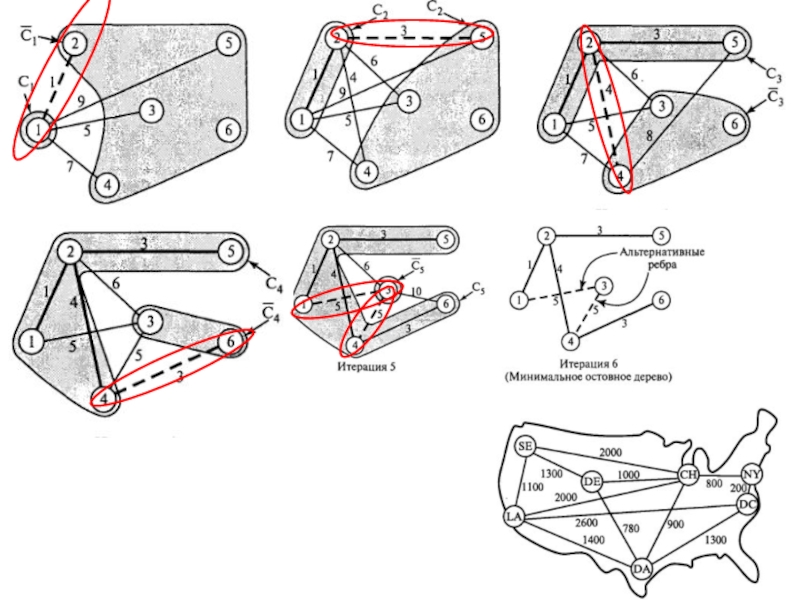
Слайд 35Задача определения кратчайшего пути
Задача определения кратчайшего пути
1
3
2
5
4
6
7
2
4
6
5
4
4
6
15
17
3
(0, - )
R
B
S
D
K
A
F
[17,S]
[5,S]
[6,S]
(5,S)
[11,A]
[9,A]
(6,S)
[8,K]
(8,K)
[12,D]
(11,A)
(12,D)
[26,R]
(16,F)
! вариант
![Задача определения кратчайшего путиЗадача определения кратчайшего пути 1325467246544615173(0, - )RBSDKAF[17,S] [5,S] [6,S] (5,S)[11,A] [9,A] (6,S)[8,K](8,K)[12,D] (11,A)(12,D)[26,R] (16,F)!](/img/tmb/2/144754/8213514f9dc9e8f65bb8357f3c29975f-800x.jpg "Введение в управление запасами Задача определения кратчайшего путиЗадача определения кратчайшего пути 1325467246544615173(0, - )RBSDKAF[17,S] [5,S]")
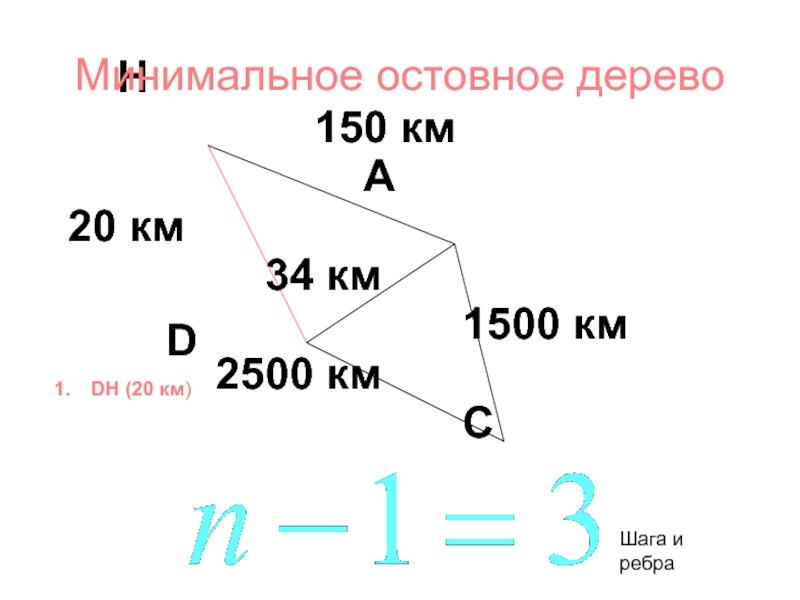
Слайд 36
кр.Пути (на неориентированном графе)
склад
3
8
60
9
3
80
9
(0;-)
600
0
9
5
50
300
3
1000
10
111
400
[число,пункт] – временная метка
(число,пункт) – постоянная метка
[9,S]
– временная метка
S
M
V
D
K
L
F
G
R
T
F
G
N
[10,S] – временная
(9,S) постоянная метка
[120,M] – временная
[17,M]
(10,S)
постоянная метка[13,D]
[1010,D]
(13,S) постоянная метка
[313,V]
(17,М) постоянная метка
(20,G)
[20,G]
(29,T)
[29,T]
(20,G)
[20,G]
(20,G)
[20,G]
(20,G)
[20,G]
(20,G)
[20,G]
G
![кр.Пути (на неориентированном графе)склад386093809(0;-)600095503003100010111400[число,пункт] – временная метка(число,пункт) – постоянная метка[9,S] – временная меткаSMVDKLFGRTFGN[10,S] – временная(9,S) постоянная метка[120,M]](/img/tmb/2/144754/48ff213fe153581842dfb6c469e21da7-800x.jpg "Введение в управление запасами кр.Пути (на неориентированном графе)склад386093809(0;-)600095503003100010111400[число,пункт] – временная метка(число,пункт) – постоянная метка[9,S] –")
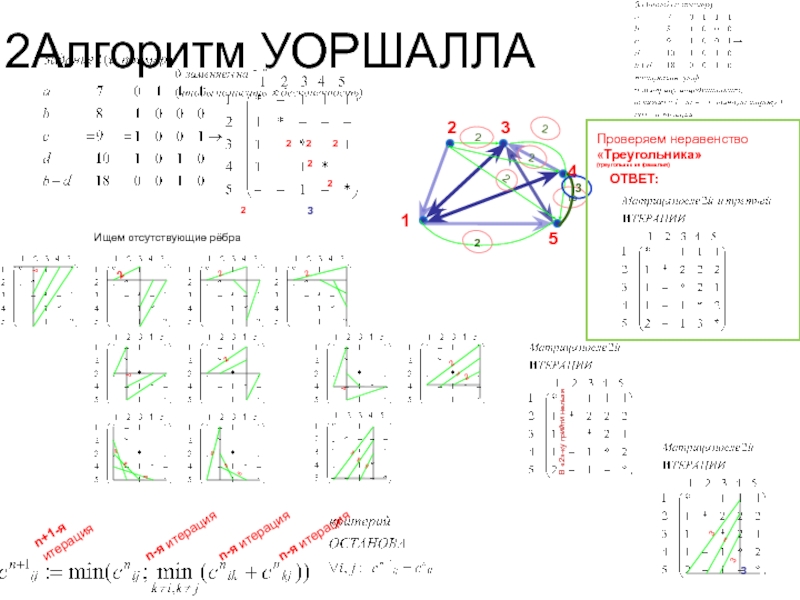
Слайд 37Алгоритм Уоршалла
a
100a
300
b
c
d
10+d
10
20
30
900
800
300
600
A
A
600
900
600
600
600
900В
1400A
320C
1700G
50E
40D
910E
A
B
C
D
E
F
G
320
50
40
910
1700
1200
900
1200
320
1700
50
40
910
D-360=40+320
D-350=30+320
360FB=min(40FD+320DB;
n-я итерация
n+1-я итерация
n-я итерация
n-я итерация
A
B
Y1
Y3
Y2
E-960=910+50
C-950=50+900
E-60=10+50
B-920=600+320
F-960=900+40
Слайд 382Алгоритм УОРШАЛЛА
1
2
5
3
4
2
Ищем отсутствующие рёбра
2
2
2
2
2
∞
∞
Проверяем неравенство «Треугольника»
(треугольник не фамилия)
2
2
∞
∞
2
2
2
∞
∞
∞
∞
∞
2
2
∞
∞
∞
2
2
2
2
2
2
В «2»-ку прийти
нельзя
3
3
∞
3
3
3
ОТВЕТ:
n-я итерация
n+1-я итерация
n-я итерация
n-я итерация
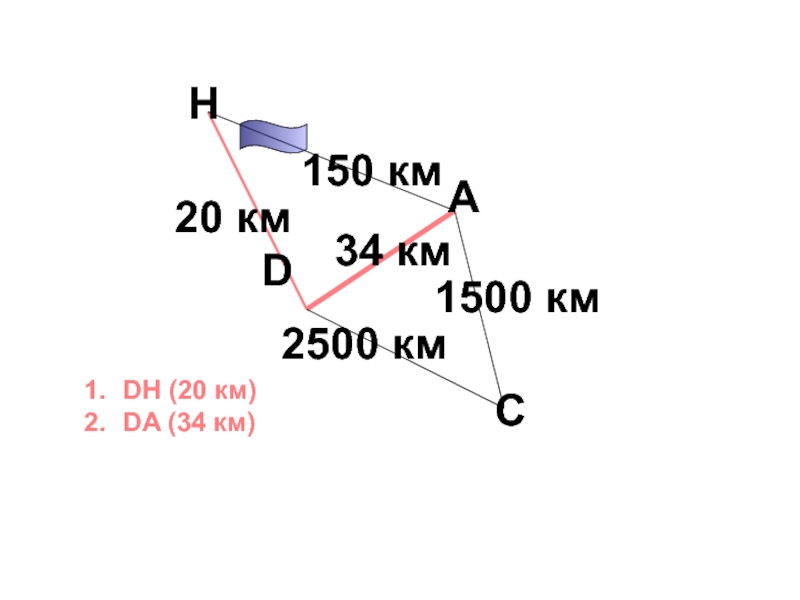
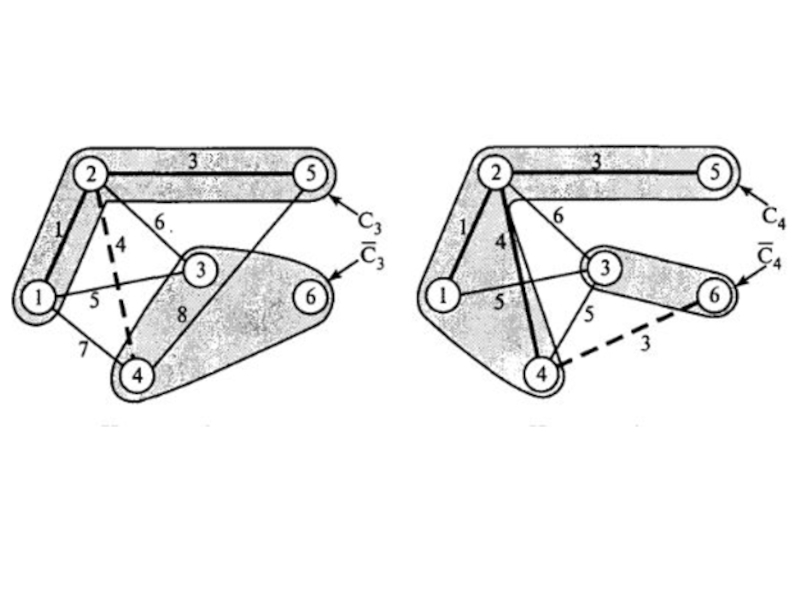
Слайд 39Кратч путь
b+c
(a+d+c)/3
|a-b|+1
0
c+1
3d+1
c+d
3b
3d-1
3(d+c)+1
3d-1
a+10
3a
d+1
|4-c|
b+c
5+a
b
a+b+c
8-a+b
Q
B
R
D
C
E
H
F
K
L
N
2
4
6
5
4
4
6
15
17
3
(0, - )
R
B
S
D
A
F
[17,S]
[5,S]
[6,S]
(5,S)
[11,A]
[9,A]
(6,S)
[8,K]
(8,K)
[12,D]
(11,A)
(12,D)
[26,R]
(16,F)
! вариант
2b
S
склад
K
москва3
Вологда
Тула
Тверь
Тула
[16,F]
K
Ответ:
B->
F->
D->
K->
S
Его длина 16 км
(0)
(1)
(2)
(3)
(4)
(5)
(6)
старт
Найти
кратчайшие пути на неориентированном графе алгоритмом ДейкстрыПользуясь метками восстановить кратчайшие пути () из 3х вершин F,K,L
![Кратч путьb+c(a+d+c)/3|a-b|+10c+13d+1c+d3b3d-13(d+c)+1 3d-1a+103ad+1|4-c|b+c5+aba+b+c8-a+bQBRDCEHFKLN246544615173(0, - )RBSDAF[17,S] [5,S] [6,S] (5,S)[11,A] [9,A] (6,S)[8,K](8,K)[12,D] (11,A)(12,D)[26,R] (16,F)! вариант2bSскладKмосква3ВологдаТулаТверьТула[16,F] KОтвет:B->F->D->K->SЕго длина](/img/thumbs/67f32c4660a231097ab0f57f10ae7d1f-800x.jpg "Введение в управление запасами Кратч путьb+c(a+d+c)/3|a-b|+10c+13d+1c+d3b3d-13(d+c)+1 3d-1a+103ad+1|4-c|b+c5+aba+b+c8-a+bQBRDCEHFKLN246544615173(0, - )RBSDAF[17,S] [5,S] [6,S] (5,S)[11,A] [9,A] (6,S)[8,K](8,K)[12,D] (11,A)(12,D)[26,R]")
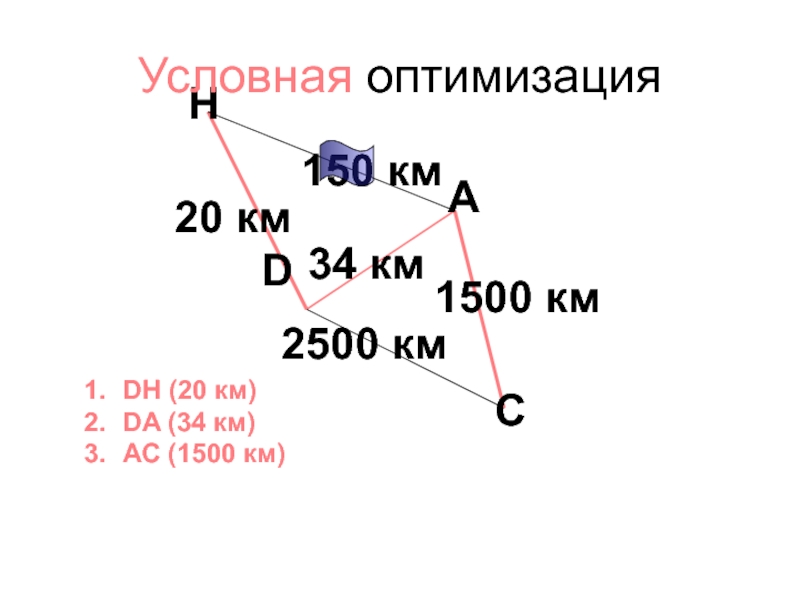
Слайд 40Образец
1
3
2
5
4
6
7
2
4
6
5
4
4
6
15
17
3
(0, - )
R
B
S
D
A
F
[17,S]
[5,S]
[6,S]
(5,S)
[11,A]
[9,A]
(6,S)
[8,K]
(8,K)
[12,D]
(11,A)
(12,D)
[26,R]
(16,F)
!
вариант
K
москва3
Вологда
Тула
Тверь
Тула
[16,F]
Ответ:
B->
F->
D->
K->
S
Его длина 16 км
(0)
(1)
(2)
(3)
(4)
(5)
(6)
![Образец1325467246544615173(0, - )RBSDAF[17,S] [5,S] [6,S] (5,S)[11,A] [9,A] (6,S)[8,K](8,K)[12,D] (11,A)(12,D)[26,R] (16,F)! вариантKмосква3ВологдаТулаТверьТула[16,F] Ответ:B->F->D->K->SЕго длина 16 км (0)(1)(2)(3)(4)(5)(6)](/img/tmb/2/144754/ad4c84404707b45605ca75ab58ee889a-800x.jpg "Введение в управление запасами Образец1325467246544615173(0, - )RBSDAF[17,S] [5,S] [6,S] (5,S)[11,A] [9,A] (6,S)[8,K](8,K)[12,D] (11,A)(12,D)[26,R] (16,F)! вариантKмосква3ВологдаТулаТверьТула[16,F] Ответ:B->F->D->K->SЕго длина 16 км (0)(1)(2)(3)(4)(5)(6)")
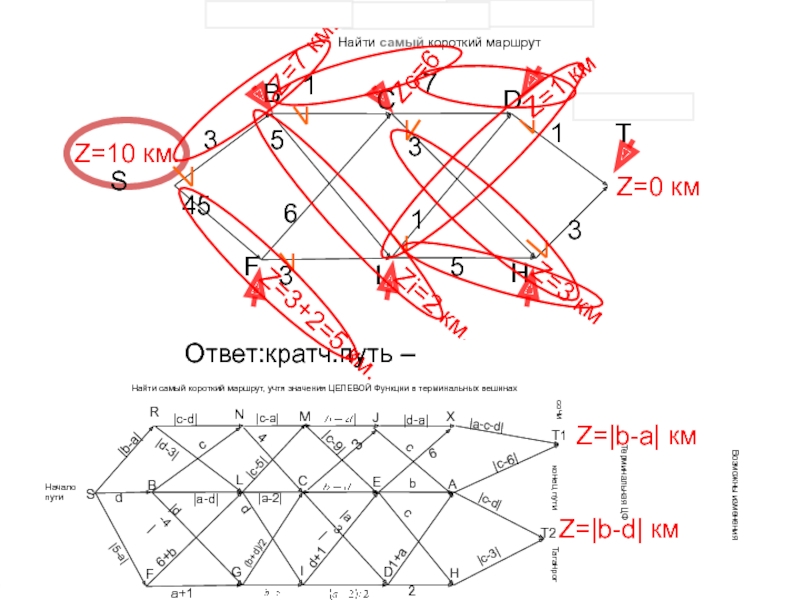
Слайд 46
Найти самый короткий маршрут
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км
Zi=2 км.
Z=1 км
Z=3 км
Zc=6
D
Z=3+2=5 км.
Z=10
км.
Z=7 км.
45
Ответ:кратч.путь – SBCHT, полная длина 10 км.
5
b
a+1
d+1
S
B
C
A
E
T3
F
I
6+b
d
d
|a-d|
2
c
(b+d)/2
|a-2|
1+а
Найти кратчайший путь
из S до T.На каждом шаге в очередном слое расставляются наименьшие возможные расстояния до Т на основе длин путей до предыдущего слоя (указаны возле стрелок) и ранее вычисленных расстояний предыдущего слоя. Результаты вычислений должны быть записаны рядом с вершинами, в противном случае в процессе проверки не возможно установить факт использования алгоритма. Кроме того, напротив каждой вершины одна из исходящих стрелок должна быть помечена как решение оптимизационной задачи поиска кратчайшего пути в этой вершине. При обратном проходе это даст возможность восстановить оптимальный путь.
L
H
G
D
|а-3|
|c-d|
|c-3|
|5-а|
d+2
|d-a|
R
M
X
J
b
|c-d|
c
|c-a|
N
|a-c-d|
|d-3|
T1
c
|c-6|
|c-9|
|c-5|
3
6
4
Z=|b-a| км
Z=|b-d| км
Начало пути
Найти самый короткий маршрут, учтя значения ЦЕЛЕВОЙ Функции в терминальных вершинах
конец пути
Терминальная ЦФ
Возможны изменения
Абхазия
Таганрог
d
T2
Z=|d-a| км
Сочи
|d-a|
Крым
|d-b|
Z=a| км
Слайд 47
Найти самый короткий маршрут
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км
Zi=2 км.
Z=1 км
Z=3 км
Zc=6
D
Z=3+2=5 км.
Z=10
км.
Z=7 км.
45
Ответ:кратч.путь – SBCHT, полная длина 10 км.
5
b
a+1
d+1
S
B
C
A
E
T2
F
I
6+b
d
d
|a-d|
2
c
(b+d)/2
|a-2|
1+а
Найти кратчайший путь
из S до T.На каждом шаге в очередном слое расставляются наименьшие возможные расстояния до Т на основе длин путей до предыдущего слоя (указаны возле стрелок) и ранее вычисленных расстояний предыдущего слоя. Результаты вычислений должны быть записаны рядом с вершинами, в противном случае в процессе проверки не возможно установить факт использования алгоритма. Кроме того, напротив каждой вершины одна из исходящих стрелок должна быть помечена как решение оптимизационной задачи поиска кратчайшего пути в этой вершине. При обратном проходе это даст возможность восстановить оптимальный путь.
L
H
G
D
|а-3|
|c-d|
|c-3|
|5-а|
|d-4|
|d-a|
R
M
X
J
|b-a|
|c-d|
c
|c-a|
N
|a-c-d|
|d-3|
T1
c
|c-6|
|c-9|
|c-5|
3
6
4
Z=|b-a| км
Z=|b-d| км
Начало пути
Найти самый короткий маршрут, учтя значения ЦЕЛЕВОЙ Функции в терминальных вешинах
конец пути
Терминальная ЦФ
Возможны изменения
сочи
Таганрог
Слайд 48
Найти самый короткий маршрут
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км
Zi=2 км.
Z=1 км
Z=3 км
Zc=6
D
Z=3+2=5 км.
Z=10
км.
Z=7 км.
45
Ответ:кратч.путь – SBCHT, полная длина 10 км.
5
|а-3|
|c-d|
|c-3|
|5-а|
d+2
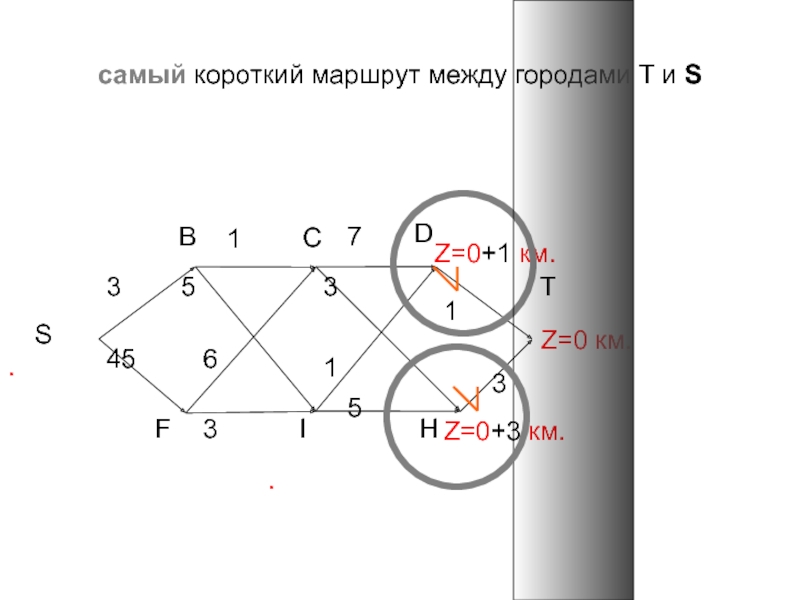
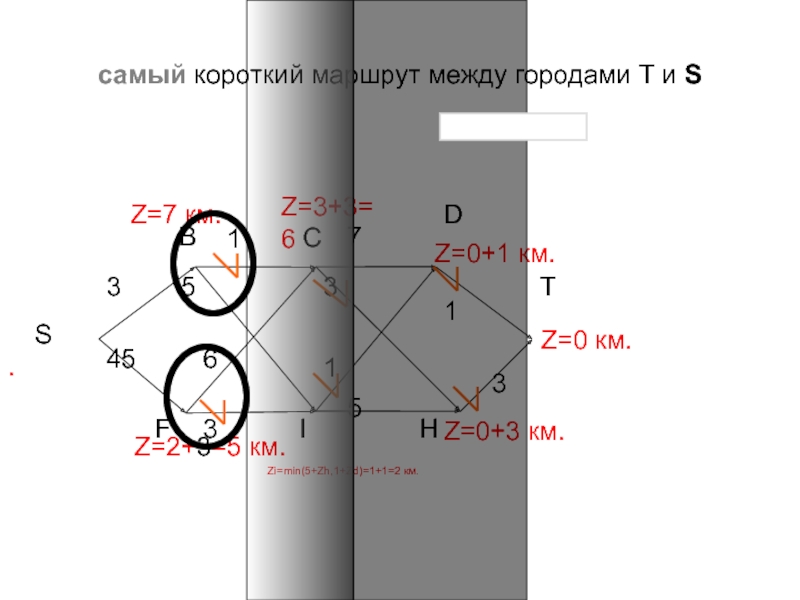
Слайд 49самый короткий маршрут между городами T и S
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км.
.
Z=0+1
км.
Z=0+3 км.
D
.
45
5
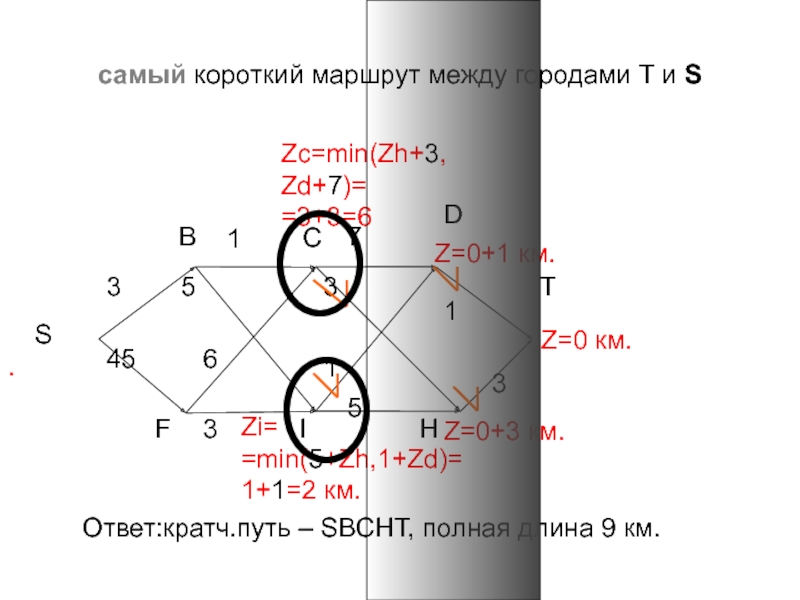
Слайд 50самый короткий маршрут между городами T и S
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км.
Zi=
=min(5+Zh,1+Zd)=
1+1=2
км.
Z=0+1 км.
Z=0+3 км.
Zc=min(Zh+3,
Zd+7)=
=3+3=6
D
.
45
Ответ:кратч.путь – SBCHT, полная длина 9 км.
5
Слайд 51самый короткий маршрут между городами T и S
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км.
Zi=min(5+Zh,1+Zd)=1+1=2
км.
Z=0+1 км.
Z=0+3 км.
Z=3+3=6
D
Z=2+3=5 км.
.
Z=7 км.
45
5
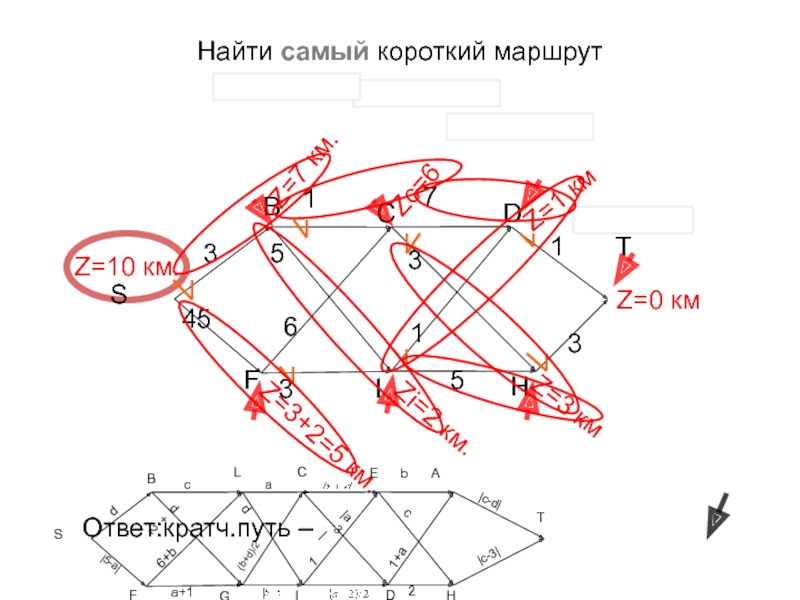
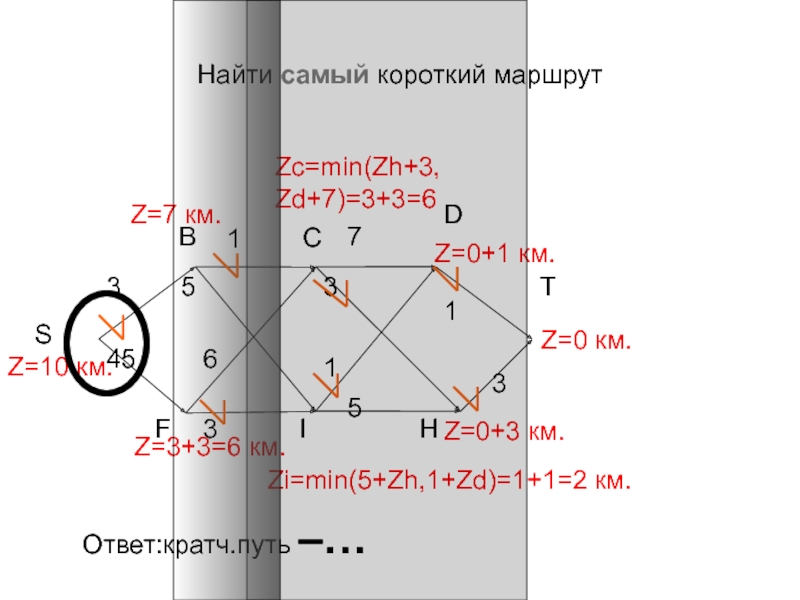
Слайд 52Найти самый короткий маршрут
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км.
Zi=min(5+Zh,1+Zd)=1+1=2 км.
Z=0+1 км.
Z=0+3 км.
Zc=min(Zh+3,
Zd+7)=3+3=6
D
Z=3+3=6 км.
Z=10
км.
Z=7 км.
45
Ответ:кратч.путь –…
5
Слайд 53Найти самый короткий маршрут
7
3
3
3
1
S
B
C
T
F
I
6
3
1
1
5
H
Z=0 км.
Zi=min(5+Zh,1+Zd)=1+1=2 км.
Z=0+1 км.
Z=0+3 км.
Zc=min(Zh+3,
Zd+7)=3+3=6
D
Z=3+3=6 км.
Z=10
км.
Z=7 км.
45
Ответ:кратч.путь – SBCHT, полная длина 10 км.
5
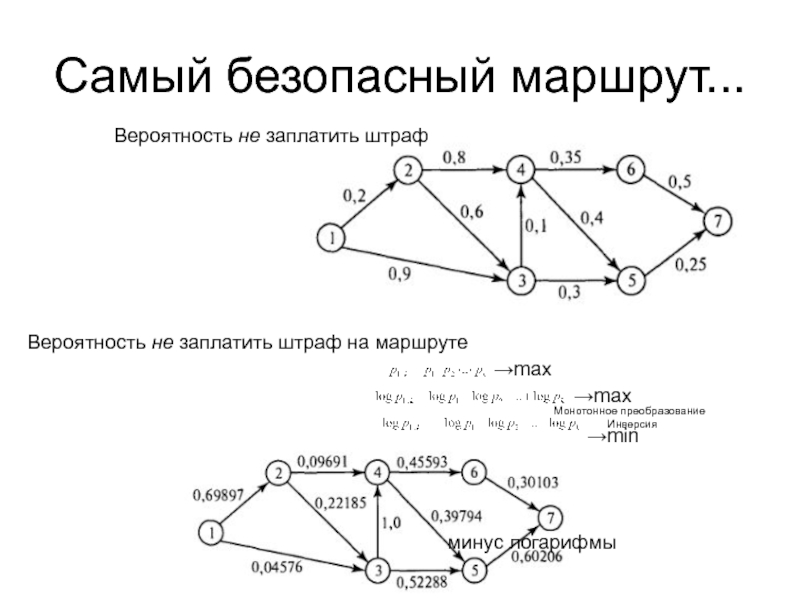
Слайд 54Самый безопасный маршрут...
Вероятность не заплатить штраф
Вероятность не заплатить штраф на
маршруте
→max
→max
минус логарифмы
Монотонное преобразование
Инверсия
→min
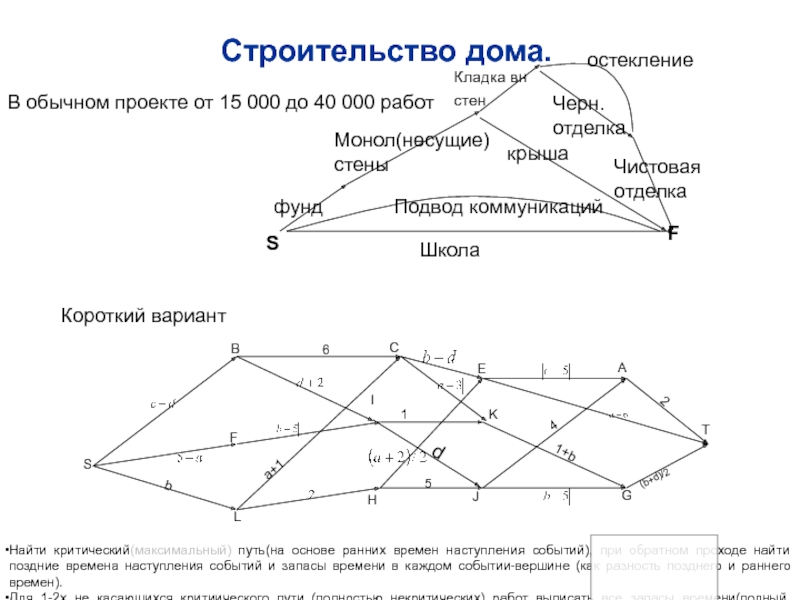
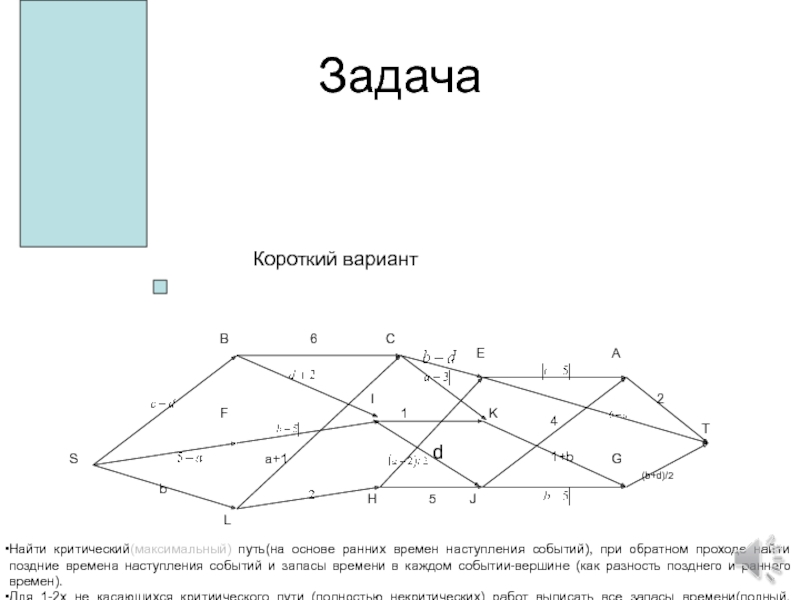
Слайд 57Строительство дома.
Школа
фунд
Монол(несущие) стены
Кладка вн стен
крыша
остекление
Черн.
отделка
Подвод коммуникаций
Чистовая
отделка
S
F
В обычном проекте
от 15 000 до 40 000 работ
Короткий вариант
d
Слайд 58Строительство дома.
Школа
фунд
Монол(несущие) стены
Кладка вн стен
крыша
остекление
Черн.
отделка
Подвод коммуникаций
Чистовая
отделка
S
F
В обычном проекте
от 15 000 до 40 000 работ
Найти критический(максимальный) путь(на основе
ранних времен наступления событий), при обратном проходе найти поздние времена наступления событий и запасы времени в каждом событии-вершине (как разность позднего и раннего времен).Для 1-2х не касающихся критиического пути (полностью некритических) работ выписать все запасы времени(полный, собственный, I и II рода). (а также коэффициенты напряженности работ).
Изобразить линейную диаграмму проекта.
b
a+1
1
K
S
B
A
E
T
F
G
|2c-2d|
J
L
6
2
1+b
4
(b+d)/2
|c-d|
|5-a|
|b-5|
d+2
|a-6|
2
1
0
фиктивная работа
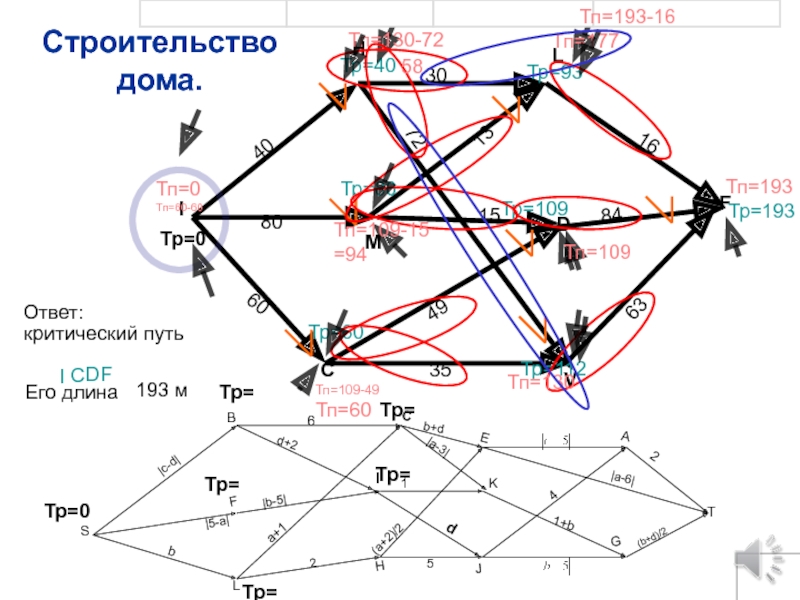
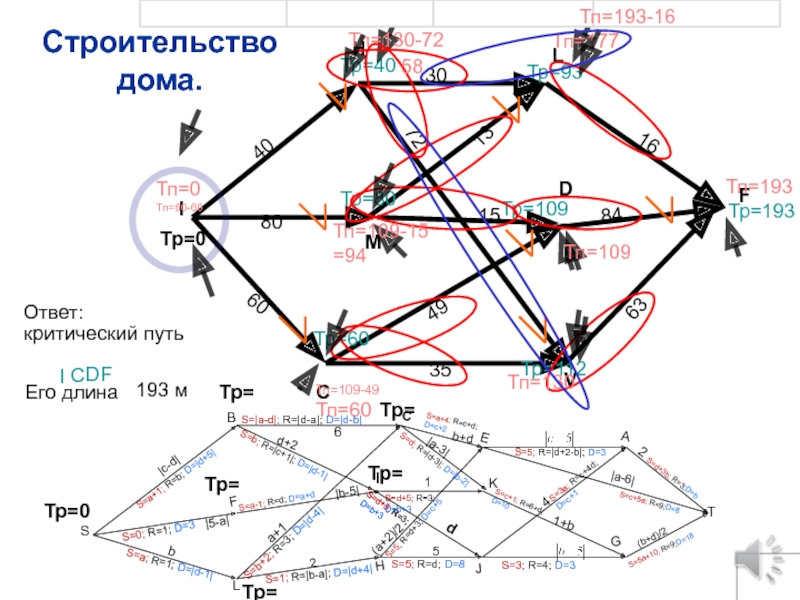
Слайд 60
критический путь
d
F
I
H
L
M
V
C
D
40
80
60
30
15
13
16
63
84
35
49
72
Тр=0
Ответ:
Тр=40
Тр=80
Тр=60
Тр=93
Тр=109
Тр=112
Тр=193
Тп=193
Тп=177
Тп=130
Тп=109
Тп=130-72
58
Тп=109-15
=94
Тп=109-49
Тп=60
Тп=0
Тп=60-60
Тп=193-16
Строительство дома.
|c-d|
|5-a|
|b-5|
d+2
|a-3|
|a-6|
(a+2)/2
b+d
2
F
D
C
I
Его длина
193 м
Тр=0
Тр=
Тр=
Тр=
Тр=
Тр=
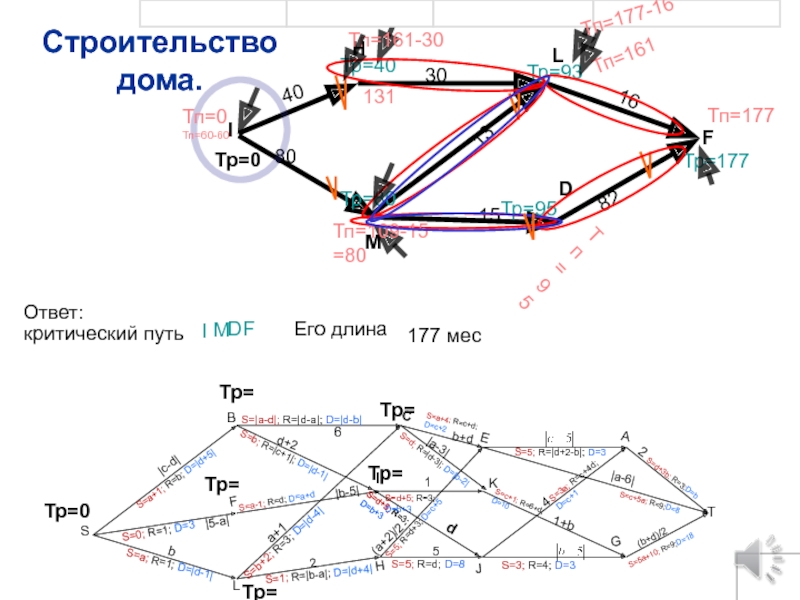
Слайд 61
критический путь
d
F
I
H
L
M
D
40
80
30
15
13
16
82
Тр=0
Ответ:
Тр=40
Тр=80
Тр=93
Тр=95
Тр=177
Тп=177
Тп=161
Тп=161-30
131
Тп=109-15
=80
Тп=0
Тп=60-60
Тп=177-16
Строительство дома.
|c-d|
|5-a|
|b-5|
d+2
|a-3|
|a-6|
(a+2)/2
b+d
2
Его длина
Тр=0
Тр=
Тр=
Тр=
Тр=
Тр=
S=a; R=1; D=|d-1|
S=1; R=|b-a|; D=|d+4|
S=b; R=|c+1|; D=|d-1|
S=a+1;
R=b; D=|d+5|
S=0; R=1; D=3
S=b+2; R=3; D=|d-4|
S=3; R=4; D=3
S=|a-d|; R=|d-a|; D=|d-b|
S=d;
R=|d-3|; D=|b-2|S=5; R=d+3; D=c+5
S=d+5; R=3;
D=b+3
S=d+5; R=3;
D=b+3
S=a-1; R=d; D=a+d
S=c+1; R=6+d;
D=10
S=5; R=d; D=8
S=5; R=|d+2-b|; D=3
S=c+5a; R=9;D=8
S=5a+10; R=9;D=18
S=d+5; R=3;
D=b+3
S=d+3b; R=3;D=b
S=a+4; R=c+d;
D=c+2
S=3a; R=c+4d;
D=c+1
Тп=95
F
D
M
I
177 мес
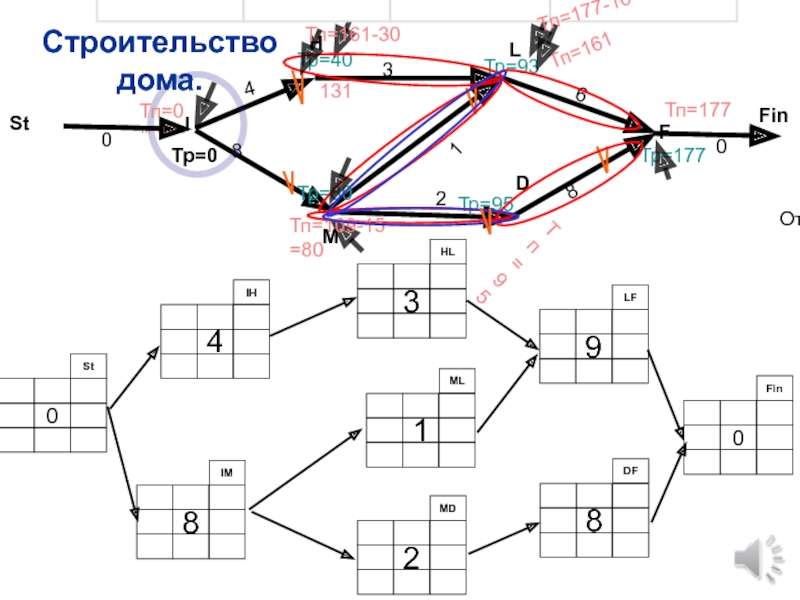
Слайд 62
критический путь
F
I
H
L
M
D
4
8
3
2
1
6
8
Тр=0
Ответ:
Тр=40
Тр=80
Тр=93
Тр=95
Тр=177
Тп=177
Тп=161
Тп=161-30
131
Тп=109-15
=80
Тп=0
Тп=60-60
Тп=177-16
Строительство дома.
Его длина
Тп=95
F
D
M
I
177 мес
St
Fin
Тп=113
Тп=96
Имя
«АВ»
tp=10 мес.
Тр=17
Тр=27
Тп=113
Тп=96
0
0
Слайд 63
критический путь
d
F
I
H
L
M
V
C
D
40
80
60
30
15
13
16
63
84
35
49
72
Тр=0
Ответ:
Тр=40
Тр=80
Тр=60
Тр=93
Тр=109
Тр=112
Тр=193
Тп=193
Тп=177
Тп=130
Тп=109
Тп=130-72
58
Тп=109-15
=94
Тп=109-49
Тп=60
Тп=0
Тп=60-60
Тп=193-16
Строительство дома.
|c-d|
|5-a|
|b-5|
d+2
|a-3|
|a-6|
(a+2)/2
b+d
2
F
D
C
I
Его длина
193 м
Тр=0
Тр=
Тр=
Тр=
Тр=
Тр=
S=a; R=1; D=|d-1|
S=1; R=|b-a|; D=|d+4|
S=b; R=|c+1|;
D=|d-1|
S=a+1; R=b; D=|d+5|
S=0; R=1; D=3
S=b+2; R=3; D=|d-4|
S=3; R=4; D=3
S=|a-d|; R=|d-a|;
D=|d-b|S=d; R=|d-3|; D=|b-2|
S=5; R=d+3; D=c+5
S=d+5; R=3;
D=b+3
S=d+5; R=3;
D=b+3
S=a-1; R=d; D=a+d
S=c+1; R=6+d;
D=10
S=5; R=d; D=8
S=5; R=|d+2-b|; D=3
S=c+5a; R=9;D=8
S=5a+10; R=9;D=18
S=d+5; R=3;
D=b+3
S=d+3b; R=3;D=b
S=a+4; R=c+d;
D=c+2
S=3a; R=c+4d;
D=c+1
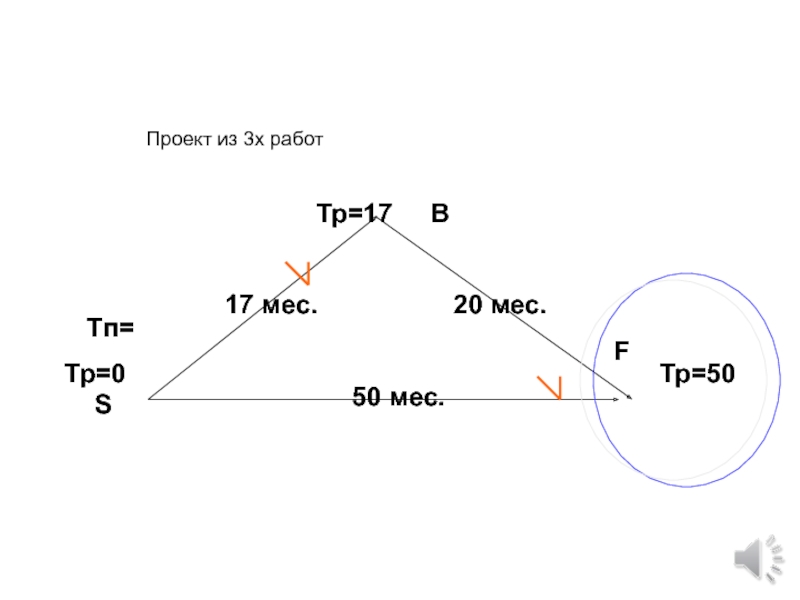
Слайд 75
120 мес.
17 мес.
20 мес.
10 мес.
24 мес.
7 мес.
Тр=0
Тп=120
Тр=17
Тр=???
Тр
S
F
B
A
Рассчитать время и запасы
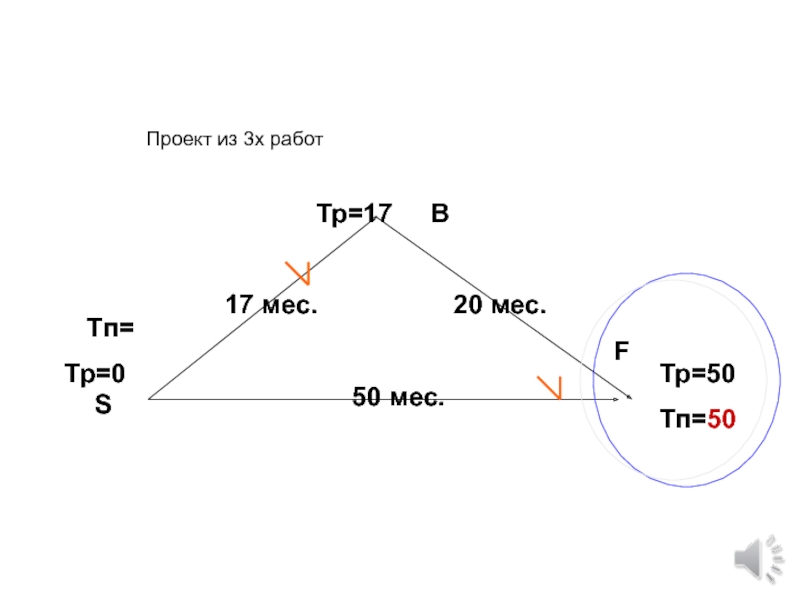
Слайд 76
120 мес.
17 мес.
20 мес.
10 мес.
24 мес.
7 мес.
Тр=0
Тп=120
Тр=17
Тр=27
Тр
S
F
B
A
Рассчитать время и запасы
Слайд 81B
A
TпН=96мес
TрН=17мес
Tпок=113мес
Tрок=27мес
Rран=27-17-10
10 мес.
Rполн=113-17-10
Rсоб=27-96-10=-79
Rпоз=113-96-10
На каждой работе вычислить
запасы
17 мес.
20 мес.
10 мес.
24 мес.
7
мес.
Тр=0
Тп=120
Тр=17
Тр=27
Тр=120
B
A
S
Тп=113
Тп=96
F
120 мес.
окончание
начало
сама работа
окончание
начало
работа
2 варианта
2 варианта
пример :
собственный
Ранний(I рода)
Поздний (II рода)
Полный зап.
Залезли
во все запасы до которых дотянулисьНе использовали запасы будущих бригад, использовав предыдущие
Не трогали чужих ЗАПАСОВ
Не использовали запасы предыдущих бригад, использовав все будущие
до которых смогли дотянуться
Поздно начали – поздно кончили
Рано начали поздно закончили
Рано начали рано закончили
Поздно начали рано закончили
Время работы
Запас
TпН=96
TрН=17
10 мес.
Tпок=113
Tрок=27
Рассчитать ВСЕ некритические работы И ХОТЯБЫ 1 Критическую
Слайд 82TпН=96
TрН=17
10 мес.
Tпок=113
Tрок=27
A
B
96
17
10 мес.
113
27
A
B
По управлению проектом
Рассчитать ВСЕ некритические работы И ХОТЯБЫ
1 Критическую
Всего 15 работ
По управлению проектом
Рассчитать ВСЕ некритические работы И
ХОТЯБЫ 1 КритическуюВсего 11/12 работ
Слайд 83
Имя
«АВ»
17 мес.
20 мес.
10 мес.
24 мес.
7 мес.
Тп=120
Тр=17
Тр=27
B
A
S
Тп=113
Тп=96
F
120 мес.
tp=10 мес.
Тр=17
Тр=27
Тп=113
Тп=96
Имя
«АВ»
tp=10 мес.
Тр
Тр
Тп
Тп
SA
BF
SF
SB
AB
AF
17
20
27
120
17
10
20
120
7
24
BF
AF
AB
График Ганта
Слайд 8417 мес.
20 мес.
10 мес.
24 мес.
7 мес.
Тп=50
Тр=17
Тр=27
B
A
S
Тп=43
Тп=26
F
50 мес.
SA
BF
SF
SB
AB
AF
17
20
27
50
17
10
20
50
7
24
BF
SF
AB
AF
Слайд 85Поздние времена последовательно вычисляются. Например, на первом шаге позднее время
может быть вычислено для события В(и ни для какого другого),
т.к. известно позднее время в точке F . чтобы успеть к позднему времени события события F и не совать график всего проекта необходимо чтобы событие В состоялось не позднее чем через Тп=120-7=113 месяцев после старта проекта. После этого можно переходить к расчету позднего времени в точке A: нужно успеть за 10 месяцев к сроку 113(В) и за 24 месяца к F (120) – итого в А Тп=min(120-24, 113-10)=96. аналогично минимизируя позднее время для S (по трём вариантам) получим 0. (Вы можете догадаться, что совпадение обоих времен на критическом пути является общей закономерностью).Решение 2) работа AB не затрагивает критический путь FS. Рассчитаем для AB все запасы времени.
В каждом событии есть два времени. Работа зависит от двух событий – значит для каждой работы имеется 4 комбинации
Собственный запас Rc=-10+27-96=-69мес.(т.е. собственного запаса нет)
Запас не претендующий на резервы предыдущих работ Rп=113-96-10=7
Запас не претендующий на резервы следующих работ Rр=27-17-10=0 мес
Наконец максимальный (полный) запас времени на работу: Rм=113-10-17=86 мес.
Слайд 87F
I
H
L
M
V
C
D
40
80
60
30
15
13
16
63
84
35
49
72
Тр=0
Критческий путь.
Ответ:
ICDF
Его длина 193 месяца
Тр=40
Тр=80
Тр=60
Тр=93
Тр=109
Тр=112
Тр=193
Тп=193
Тп=177
Тп=193-16
Тп=130
Тп=109
Тп=130-72
58
Тп=109-15
=94
Тп=109-49
Тп=60
Тп=0
Тп=60-60
Слайд 88Замена оборудования
Уст. Оборудование теряет в стоимости:
1й год стоимость 4000, послед
года 2 р меньше
2й год – 2000р
3й год – 1000р
4й
год -500 р и т.д.
Издержки функ: 600р*число лет
(время 5 лет)
Граничное условие
продажа оборудования
продажа
продажа
продажа
продажа
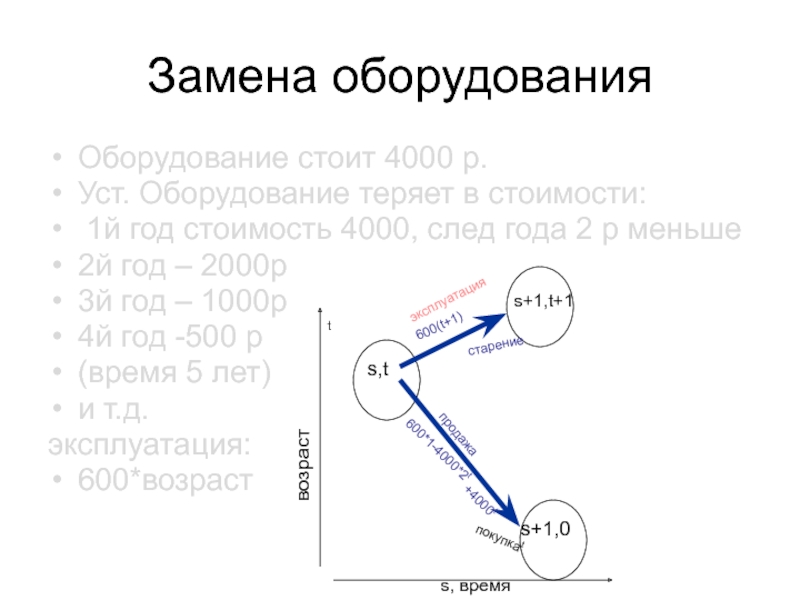
Ответ: эксплуатировать три года, потом заменить и не менять 2 года, прибыль 11 900 р .
Слайд 89Замена оборудования
Оборудование стоит 4000 р.
Уст. Оборудование теряет в стоимости:
1й год стоимость 4000, след года 2 р меньше
2й год
– 2000р3й год – 1000р
4й год -500 р
(время 5 лет)
и т.д.
эксплуатация:
600*возраст
возраст
продажа
600(t+1)
600*1-4000*2t
+4000t
покупкаt
t
s, время
s,t
s+1,t+1
s+1,0
старение
эксплуатация
Слайд 91F
I
H
L
M
V
C
D
40
80
60
30
15
13
16
63
84
35
49
72
Тр=0
Крит. Путь.
Тр=40
Тр=80
Тр=60
Тр=80+13=max(TpM+ML;TpH+HL)
Тр=49+60=max(TpM+MD;TpC+CD)
Тр=40+72=max(TpH+HV;TpC+CV)
Тр=93
Тр=109
Тр=112
Тр=193
Слайд 92F
I
H
L
M
V
C
D
40
80
60
30
15
13
16
63
84
35
49
72
Тр=0
Крит. Путь.
Тр=40+0
Тр=80+0
Тр=60+0
Тр=93=max(TpM+ML;TpH+HL)
Тр=109=max(TpM+MD;TpC+CD)
Тр=40+72=max(TpH+HV;TpC+CV)
Тр=109+84=193=
=max
(TpL+LF;
TpD+DF;
TpV+VF)
Тр=193
Слайд 102метод потенциалов
транспортная задача
Метод минимального элемента , Метод Северо-западного
угла и
Слайд 103Условие:
.
решение:
Исходное решение построить методом минимального элемента. Найти потенциалы,
(repeat пока не достигните успеха): построить цикл пересчёта, переходя к
новому решению вплоть до нахождения оптимума. (Методом потенциалов вновь и вновь проверять оптимальность – критерий оптимальности – отсутствие отрицательных ЦЕН поставок вне базисного плана после применения потенциалов на очередной итерации).Вычислить Целевую функцию, записать в ответе значение ЦФ и оптимальный план.
(1,5/2 уз)
(
Задача оценивается в зависимости от сложности решения
Слайд 104
столбцы
строки
Склады(поставщики)
Терминалы //потребители
Суммарные издержки
источник
потребители
сток
ограничения
n+m штук
n+m-1 ненулевых поставок
по числу независимых ограничений
1 ограничение лишнее
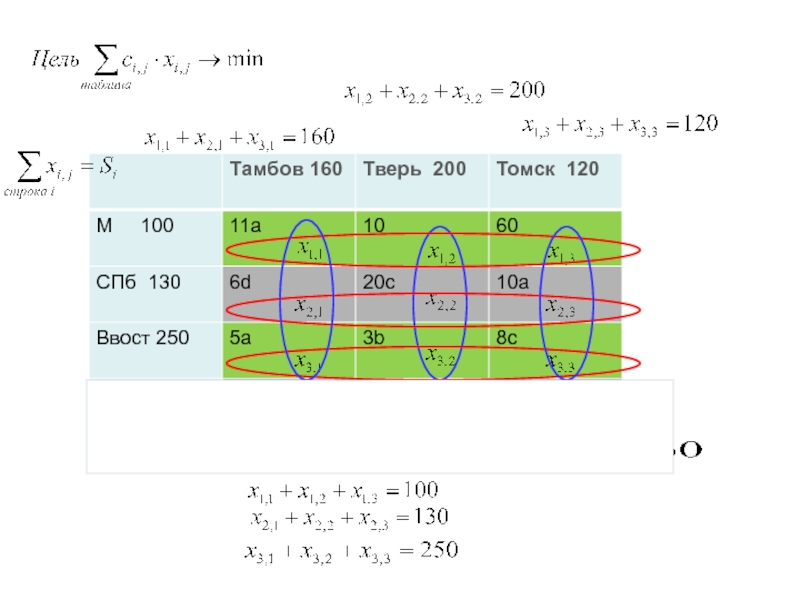
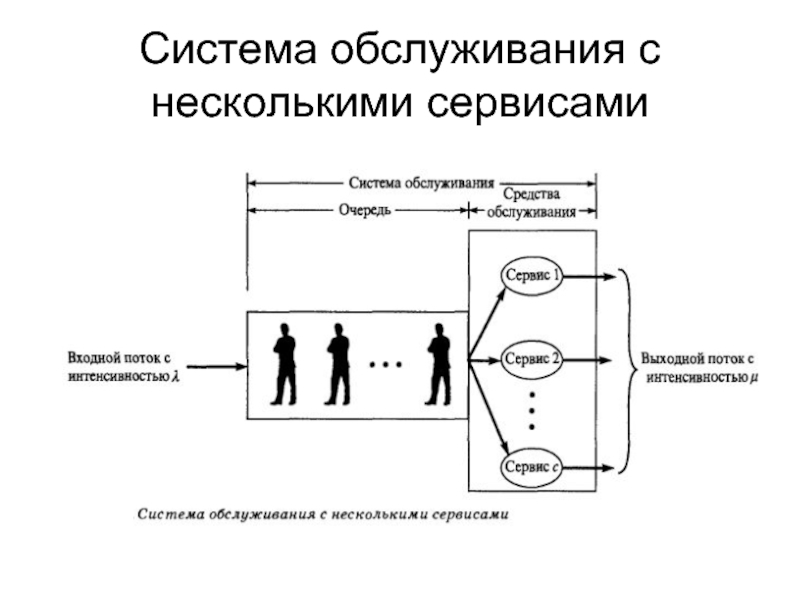
Слайд 108Транспортная задача
Мin(100,200)=100
Мin(120,100)=100
Мin(20,300)=20
Мin(240,280)=240
Мin(160,40)= 40
Мin(120,120)=120
Метод Северо-Западного Угла
(0)
(0)
(0)
(0)
(0)
(0)
(0)
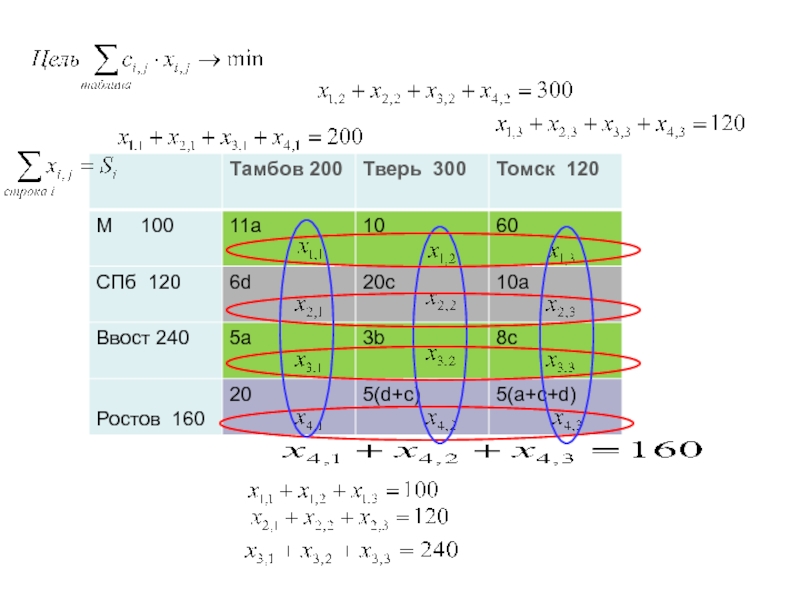
Слайд 109Транспортная задача
Мin(120,200)=120
Мin(160,300)=160
Мin(100,80)=80
Мin(240,120)=120
Мin(120,140)=120
Мin(20, 20)=20
Метод минимального элемента
80
140
20
120
20
(0)
(0)
(0)
(0)
(0)
(0)
(0)
Слайд 110Транспортная задача
x21= 120
x42= 160
x11=80
x33= 120
x32= 120
x12= 20
Метод Потенциалов
таможня
Вывозные пошлины
Ввозные пошлины
Новые
тарифы
Слайд 111Транспортная задача
x21= 120 .
x42= 160
x11=80
x33= 120
x32= 120
x12= 20
.
Цикл ПЕРЕСЧЁТА
На сколько поставки падают в начале стрелок
на столько они возрастают на их концах!!Берём минимальный вдоль цикла источник (отрицательный элемент)
+
+
-
-
В минусах поставка падает
В плюсах поставка растёт
Считаем минимум среди минусов (падает не ниже 0)
Слайд 113«Теорема».
Для каждой базисной переменной существует ровно один означенный цикл
данного типа проходящий через неё и базисные переменные.
Слайд 114Транспортная задача
x21= 100
x42= 160
x11=100
x33= 120
x32= 120
x22= 20
Метод Потенциалов
таможня
Рассчитаем новые тарифы
Данный план оптимален
Отрицательных тарифов нет
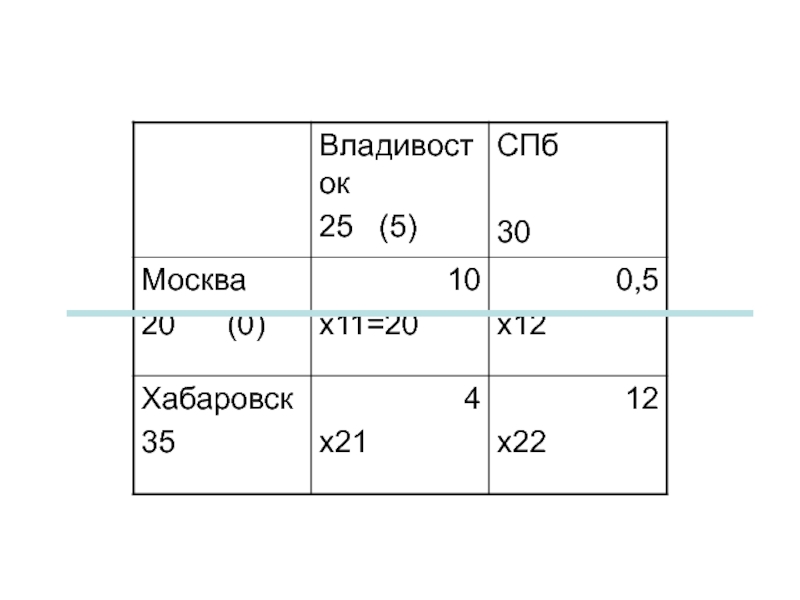
Слайд 120БАЗИСНЫЙ ПЛАН: значение ЦФ/ Лучше возможно?!
Выбираем небазисную переменную
Уменьшаем целевую функцию
до бесконечности?
Слайд 121Лучше возможно?!: Двойственная задача и метод потенциалов
Выбираем небазисную переменную
Уменьшаем целевую
функцию до бесконечности?
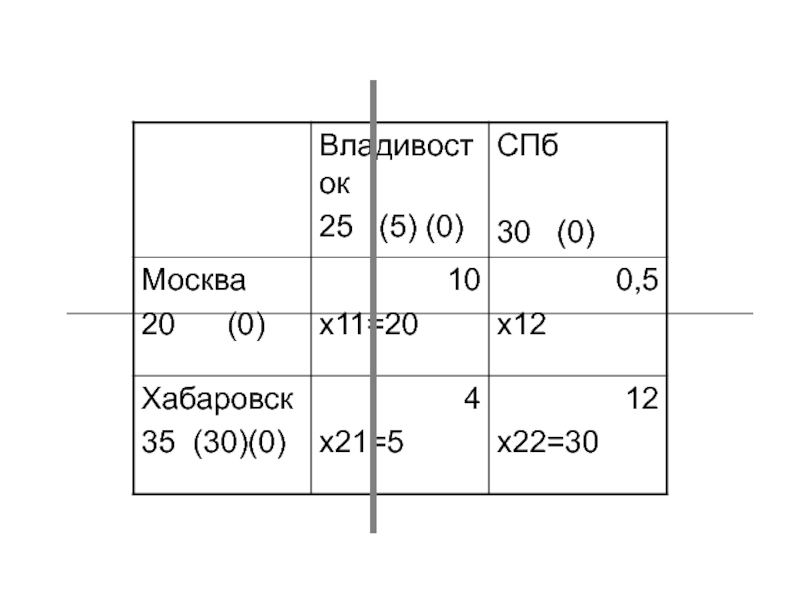
Слайд 122Уменьшаем целевую функцию до бесконечности?
Т.к. уменьшающиеся поставки должны остаться положительными
Слайд 123Лучше возможно?!: v+u=0 потенциалы есть +- пошлина производителя и
импортера – не зависит от x и не меняет предпочтения
задачиВыбираем небазисную переменную
Слайд 127Лучше возможно?!:
потенциалы подобрали так v+u=0 на базисных переменных
Выбираем небазисную
переменную
Слайд 128Лучше возможно?!: v+u=0 потенциалы есть +- пошлина производителя и
импортера – не зависит от x и не меняет предпочтения
задачиВыбираем небазисную переменную
Слайд 129Лучше возможно?!: v+u=0 потенциалы есть +- пошлина производителя и
импортера – не зависит от x и не меняет предпочтения
задачиВыбираем небазисную переменную
Слайд 147
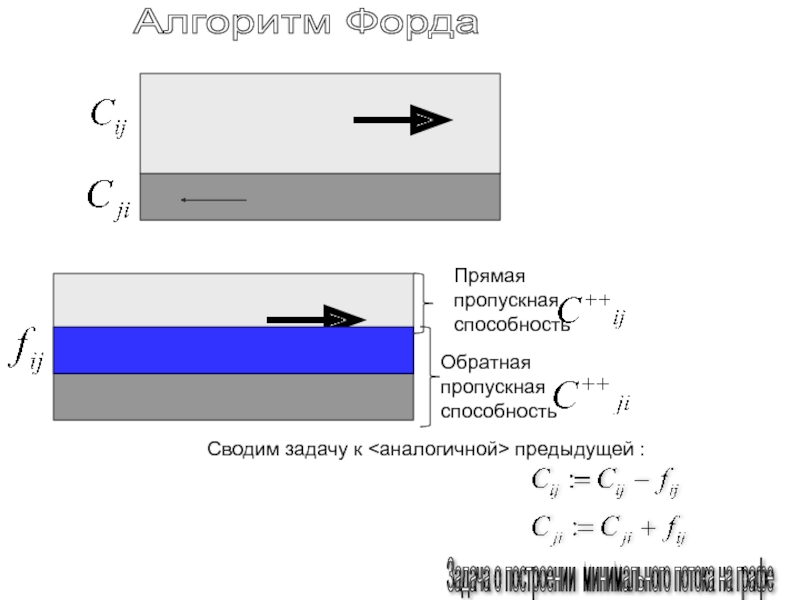
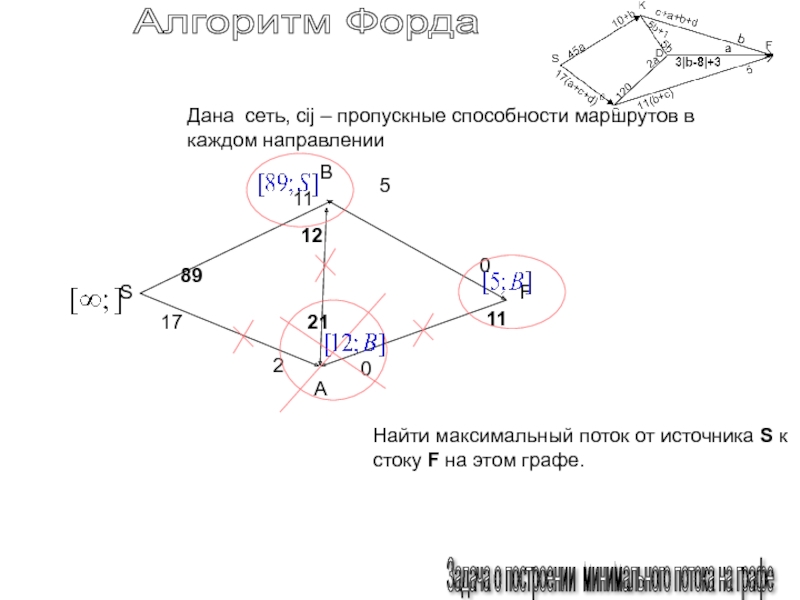
Алгоритм Форда
Задача о построении минимального потока на графе
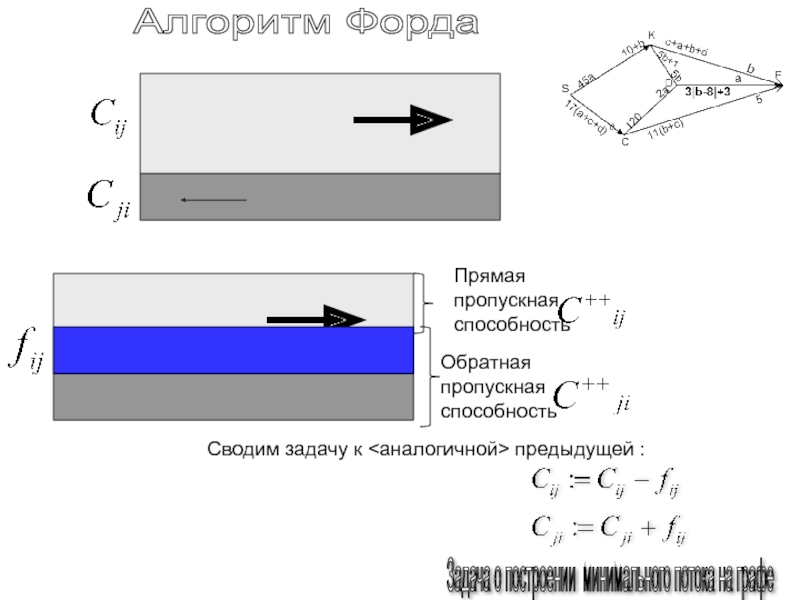
Обратная
пропускная способность
Прямая пропускная способность
Сводим задачу к предыдущей :
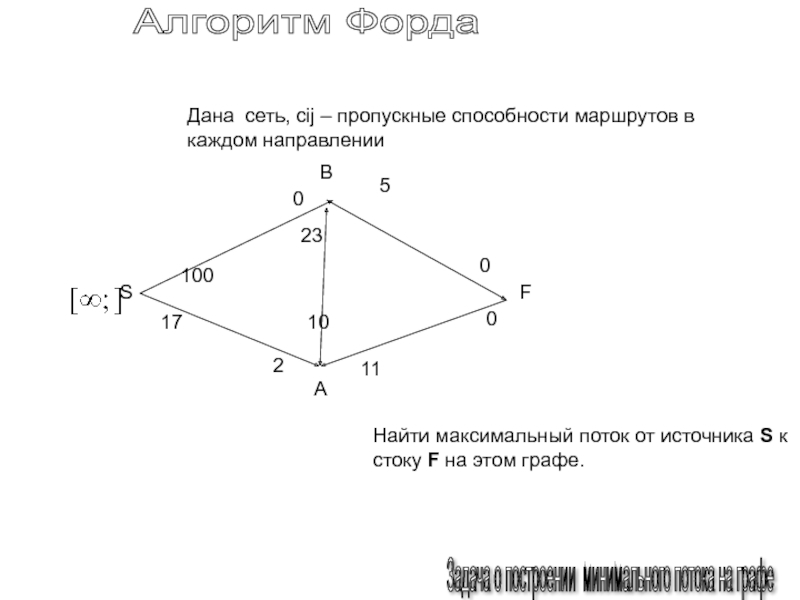
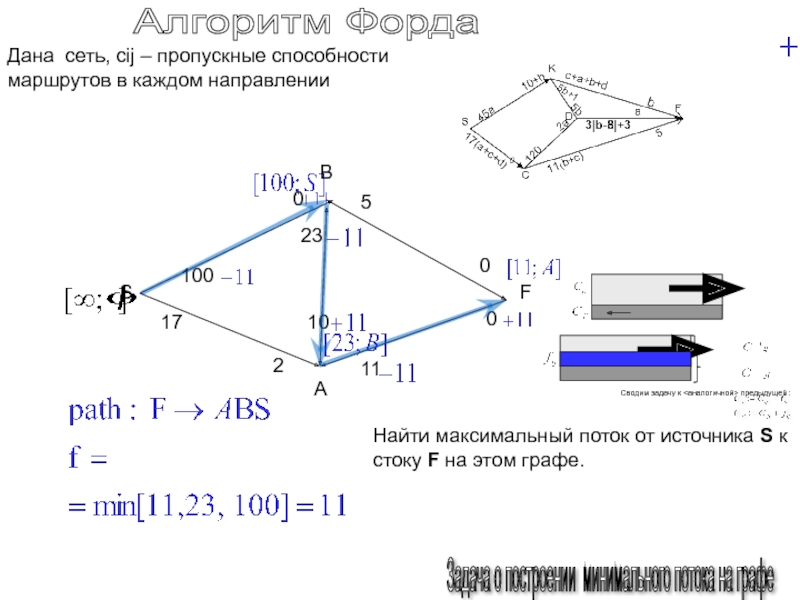
Слайд 148Алгоритм Форда
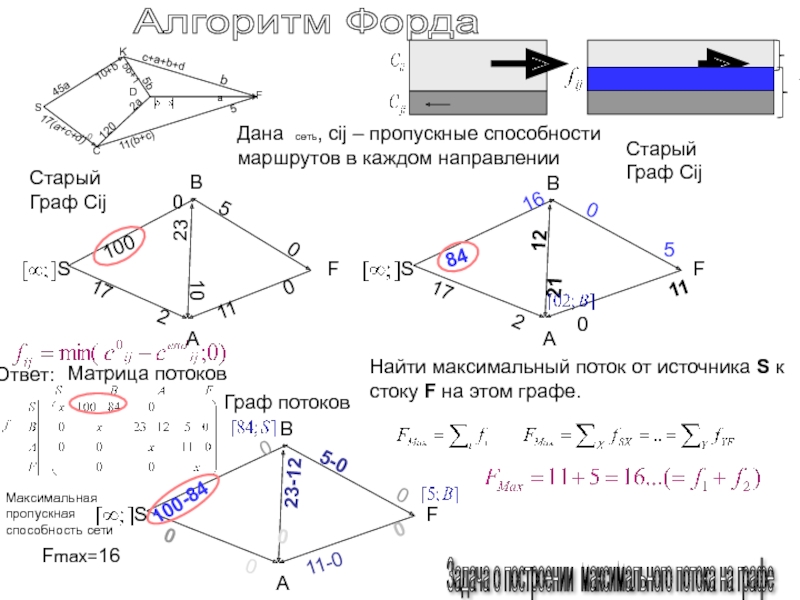
Задача о построении минимального потока на графе
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.
Слайд 149Алгоритм Форда
Задача о построении минимального потока на графе
100
11
17
5
23
10
0
0
S
F
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.0
2
B
A
Слайд 150Алгоритм ФОРДА
Задача о построении минимального потока на графе
89
0
17
5
12
21
0
11
S
F
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.11
2
B
A
Слайд 151Алгоритм Форда
Задача о построении минимального потока на графе
89
0
17
5
12
21
0
11
S
F
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.11
2
B
A
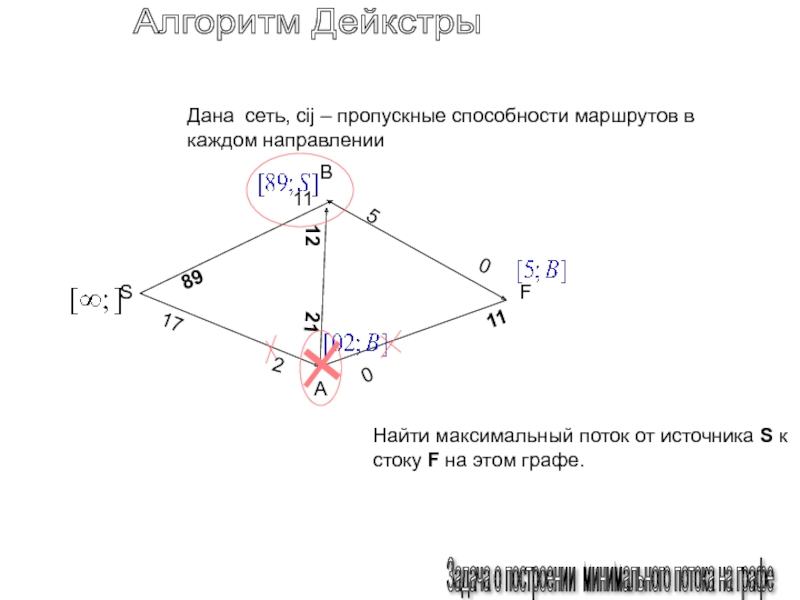
Слайд 152Алгоритм Дейкстры
Задача о построении минимального потока на графе
89
0
17
5
12
21
0
11
S
F
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.11
2
B
A
Слайд 153Алгоритм Форда
Задача о построении минимального потока на графе
89
0
17
5
02
21
0
11
S
F
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.11
2
B
A
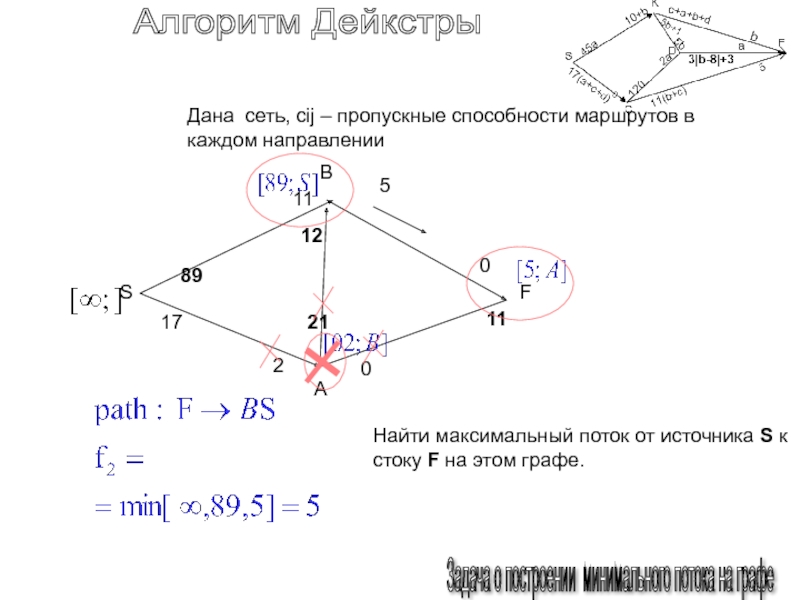
Слайд 154Алгоритм Дейкстры
Задача о построении минимального потока на графе
89
0
17
5
12
21
0
11
S
F
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.11
2
B
A
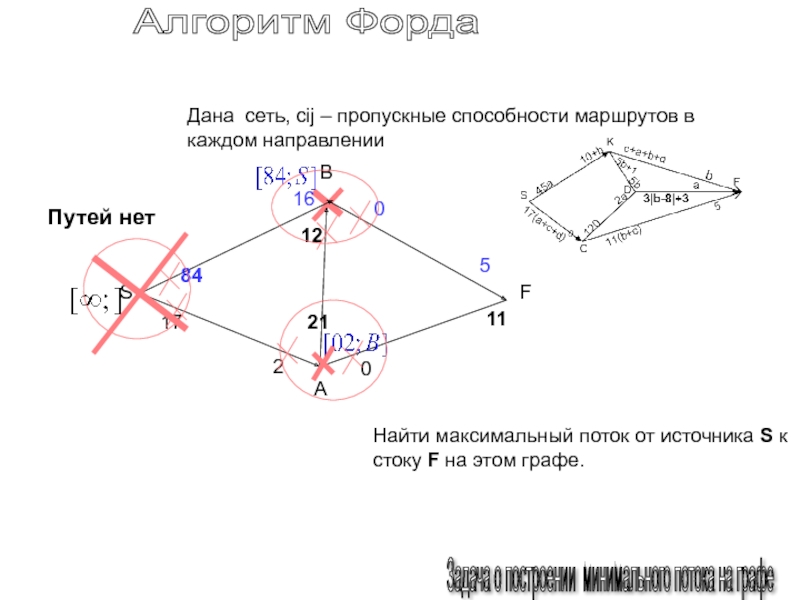
Слайд 155Алгоритм Форда
Задача о построении минимального потока на графе
84
0
17
0
12
21
5
11
S
F
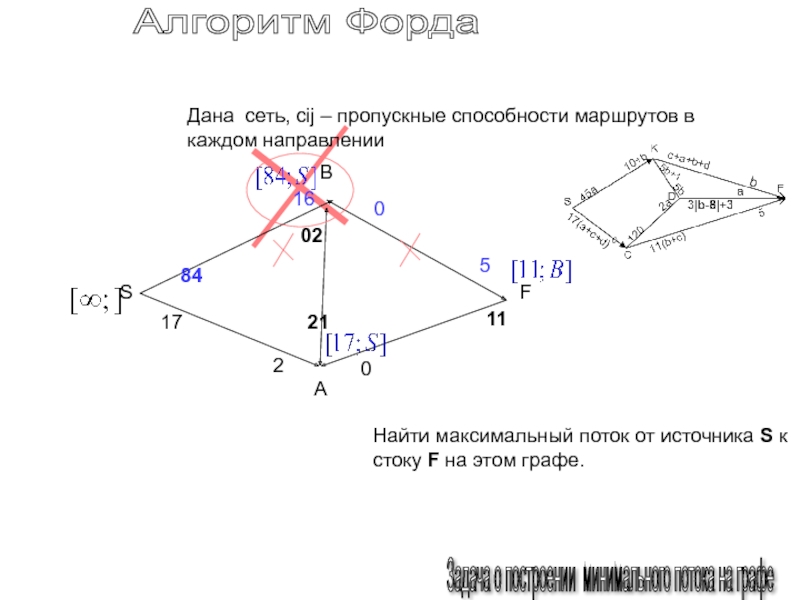
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.16
2
B
A
Путей нет
Слайд 156Алгоритм Форда
Задача о построении максимального потока на графе
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.100
11
17
5
23
10
0
0
S
F
0
2
B
A
100-84
11-0
0
5-0
23-12
0
0
0
S
F
0
0
B
A
Обратная пропускная способность
Прямая пропускная способность
b
0
Ответ:
Матрица потоков
Максимальная пропускная способность сети
Fmax=16
Старый
Граф Сij
Старый
Граф Сij
Граф потоков
Слайд 157Алгоритм Форда
Задача о построении минимального потока на графе
84
0
17
0
02
21
5
11
S
F
Дана
сеть, cij – пропускные способности маршрутов в каждом направлении
Найти
максимальный поток от источника S к стоку F на этом графе.16
2
B
A
Слайд 158Алгоритм Дейкстры
Задача о построении минимального потока на графе
84
0
17
0
12
21
5
11
S
F
Дана
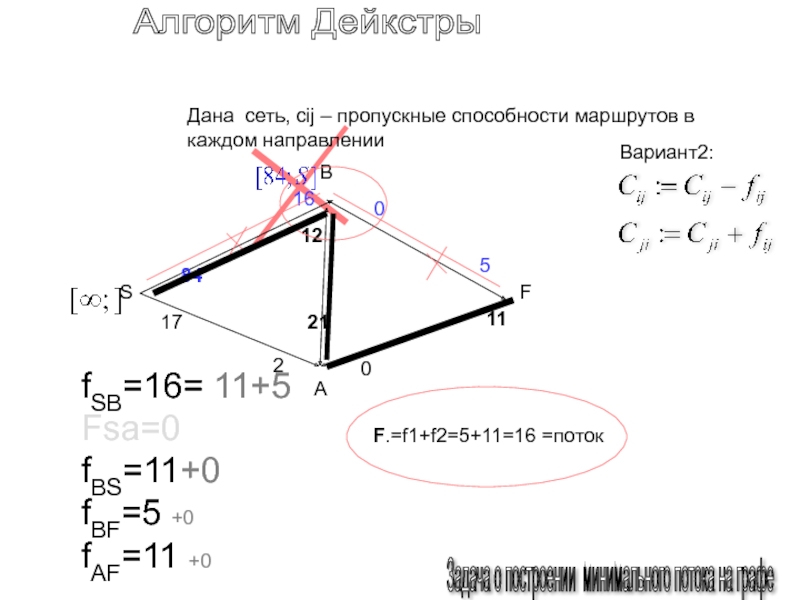
сеть, cij – пропускные способности маршрутов в каждом направлении
F.=f1+f2=5+11=16
=поток16
2
B
A
fSB=16= 11+5
Fsa=0
fBS=11+0
fBF=5 +0
fAF=11 +0
Вариант2:
Слайд 159
Алгоритм Форда
Задача о построении минимального потока на графе
Обратная
пропускная способность
Прямая пропускная способность
Сводим задачу к предыдущей :
Слайд 171
критический путь
F
I
H
L
M
D
40
80
30
15
13
16
82
Тр=0
Ответ:
Тр=40
Тр=80
Тр=93
Тр=95
Тр=177
Тп=177
Тп=161
Тп=161-30
131
Тп=109-15=80
Тп=0
Тп=60-60
Тп=177-16
Строительство дома.
Его длина
Тп=95
F
D
M
I
177 мес
