Слайд 1Выбор передаточных чисел узлов трансмиссии
Общее число передач или ступеней трансмиссии
(nст тр) определяется произведением числа ступеней в отдельных агрегатах:
nст тр
= nст дел ∙ nст к.п ∙ nст дем ∙ nст р.к
Чем больше число ступеней передач nст тр, тем выше тягово-скоростные и топливно-экономические характеристики колесной машины.
Слайд 2Выбор передаточных чисел узлов трансмиссии
Это можно проиллюстрировать на примере КМ
с двумя коробками перемены передач: 2-х и 5-и ступенчатой, у
которых передаточные числа крайних передач равны:
uI2 = uI5
uII2 = uV5
Слайд 3Выбор передаточных чисел узлов трансмиссии
При сопротивлении ψ1 для 5-ти ступенчатой
КП возможна работа на II5 передаче при полной подаче топлива
со скоростью v1.5. А для 2-х ступенчатой возможна работа только на I2 передаче на частичной характеристике (пунктирная линия) со скоростью v1.2.
Скорость v1.5 > v1.2, а также больше коэффициент использования мощности у 5-ти ступенчатой коробки kиN5 > kиN2, следовательно, расход топлива меньше.
Слайд 4Выбор передаточных чисел узлов трансмиссии
При одинаковой устано-вившейся скорости v2 при
коэф. сопротивления ψ2 машина с 5-ти ступенчатой коробкой и работе
на V5 передаче способна при переходе на IV5 передачу разгоняться и увеличивать скорость.
Для 2-х ступенчатой коробки это невозможно.
Слайд 5Выбор передаточных чисел узлов трансмиссии
При той же одинаковой скорости v2
и возрастании коэф. сопротивления движению до ψ3 машина с 5-ти
ступенчатой коробкой способна сохранять ту же скорость при переходе на IV5 передачу.
Машина с 2-х ступенчатой КП вынуждена переходить на низшую передачу I2, работать на частичной характеристике двигателя (пунктирная линия) и значительно снизить скорость v2.2.
Слайд 6Выбор передаточных чисел узлов трансмиссии
Однако увеличение nст тр значительно усложняет
конструкцию трансмиссии и повышает (без автоматического их переключения) напряженность труда
водителя. Количество ступеней nст тр зависит от необходимого диапазона передаточных чисел Dтр, удельной мощности двигателя и назначения КМ.
Слайд 7Выбор передаточных чисел узлов трансмиссии
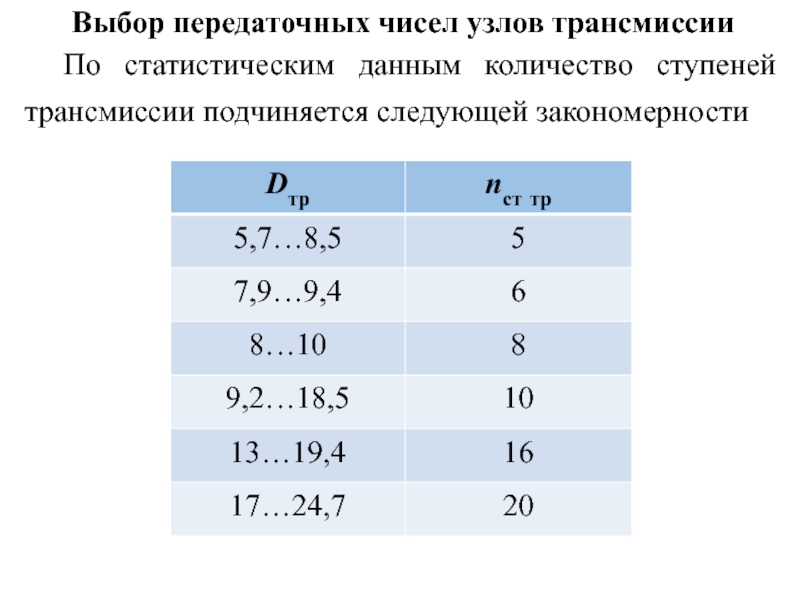
По статистическим данным количество ступеней трансмиссии
подчиняется следующей закономерности
Слайд 8Выбор передаточных чисел узлов трансмиссии
Количество ступеней базовой коробки передач nст
к.п обычно не превышает шести. При большем их количестве затрудняется
возможность обеспечения необходимой жесткости валов, так как увеличивается их длина.
Обеспечение необходимого диапазона трансмиссии достигается за счет других агрегатов.
Слайд 9Выбор передаточных чисел КП
Минимальное передаточное число в КП обычно принимается
равным единице:
uк.п min = 1
Максимальное передаточное число в
КП определяется при известном uтр.max:
uк.п.max = uтр.max/(uдел1∙uдем1∙uр.к1∙uг.п∙uк.р)
Слайд 10Выбор передаточных чисел КП
Передаточные числа промежуточных передач выбираются из условия
обеспечения оптимальных показателей тягово-скоростных и топливно-экономических свойств КМ.
Существуют различные методики
их выбора: наиболее полное использование мощности двигателя; получение наилучших разгонных характеристик; оптимальной топливной экономичности, наибольшей скорости в заданных условиях движения, комплексные методики и т. д.
Слайд 11Выбор передаточных чисел КП
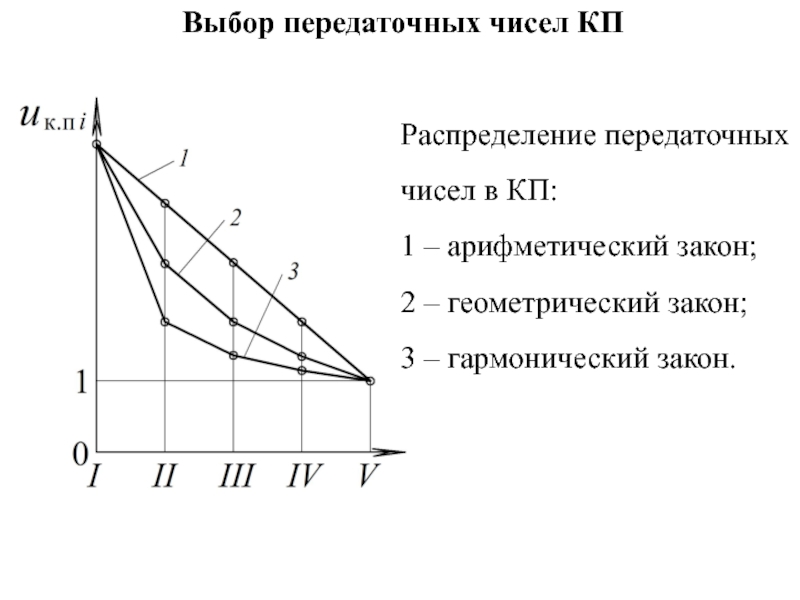
Распределение передаточных чисел в КП:
1 – арифметический
закон;
2 – геометрический закон;
3 – гармонический закон.
Слайд 12Выбор передаточных чисел КП
1. Закон арифметической прогрессии:
uк.п I - uк.п
II = … = uк.п(m-1) - uк.пm = qариф =
const
Постоянная арифметического ряда
qариф = (uк.пI - uк.пm)/(m - 1).
Слайд 13Выбор передаточных чисел КП
2. Закон геометрической прогрессии обеспечивает работу КМ
в узком диапазоне оборотов, в зоне максимальной мощности, без учета
падения скорости при переключении передач
uк.п(i+1) / uк.п i = nдв.1/nдв.2 = qгеом = const.
Слайд 14Выбор передаточных чисел КП
В общем виде для геометрического ряда передаточное
число i-й передачи в КП с числом ступеней m определяется
выражением:
По этому выражению можно получить передаточное число и для ускоряющей передачи uк.п (m+1) , однако оно получается значительно меньше, чем используется на практике (0,7…0,8).
Слайд 15Выбор передаточных чисел КП
Если учитывать падение скорости при переключении передач
(ΔVпер ≠ 0), а также для лучшего использования мощности двигателя
целесообразно сближать передаточные числа высших передач:
Слайд 16Выбор передаточных чисел КП
Это условие может обеспечиваться при использовании гармонического
ряда
Подобрать в КП ряд передаточных чисел, строго соответствующих геометрическому или
гармоническому ряду, практически не представляется возможным из-за дискретности чисел шестерен, определяющих реальные значения передаточных чисел, поэтому они могут незначительно отличаться от расчетных.
Слайд 17Выбор передаточных чисел КП
Передаточные числа могут также быть скорректированы для
обеспечения каких-либо оптимальных эксплуатационных параметров.
Например, для обеспечения максимального ускорения, используя
упрощенную схему трансмиссии, не учитывающую податливость и демпфирование узлов трансмиссии
Слайд 18Выбор передаточных чисел КП
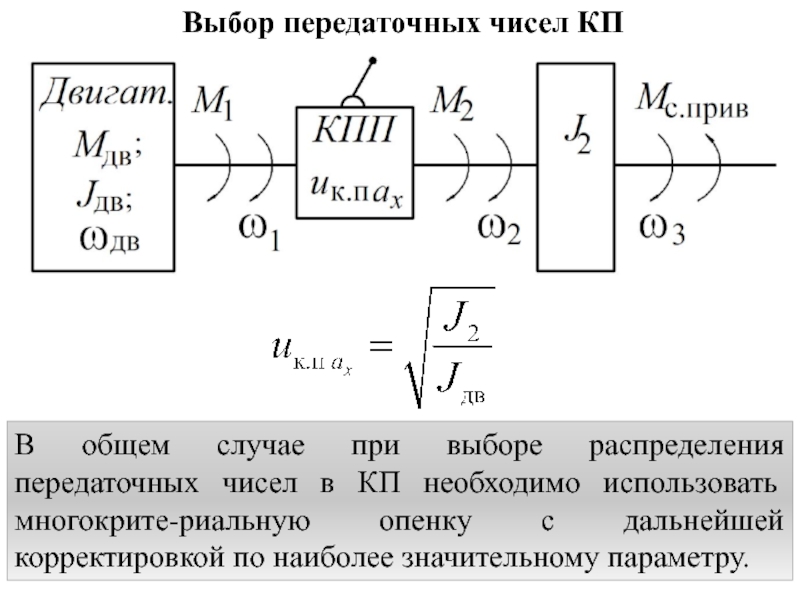
В общем случае при выборе распределения передаточных
чисел в КП необходимо использовать многокрите-риальную опенку с дальнейшей корректировкой
по наиболее значительному параметру.
Слайд 19Выбор схемы трансмиссии или привода КД
Принято рассматривать:
неполноприводные КМ, которые обеспечивают
минимальные затраты энергии при движении по твердым опорным поверхностям (ОП)
с высоким коэф. сцепления.
полноприводные КМ, обеспечивающие высокие тяговые возможности на деформируемых ОП и твердых ОП с малым коэф. сцепления.
Слайд 20Выбор схемы трансмиссии или привода КД
Суммарные потери в автомобиле определяются
суммой потерь в трансмиссии и на колесных движителях.
Чем больше узлов
трансмиссии, тем ниже ее КПД и выше потери. Особенно велики потери при блокированной схеме трансмиссии (ωкi = const) при движении по твердым ОП и малом сопротивлении движению, когда возможно возникновение циркуляции мощности.
Слайд 21Потери в колесном движителе
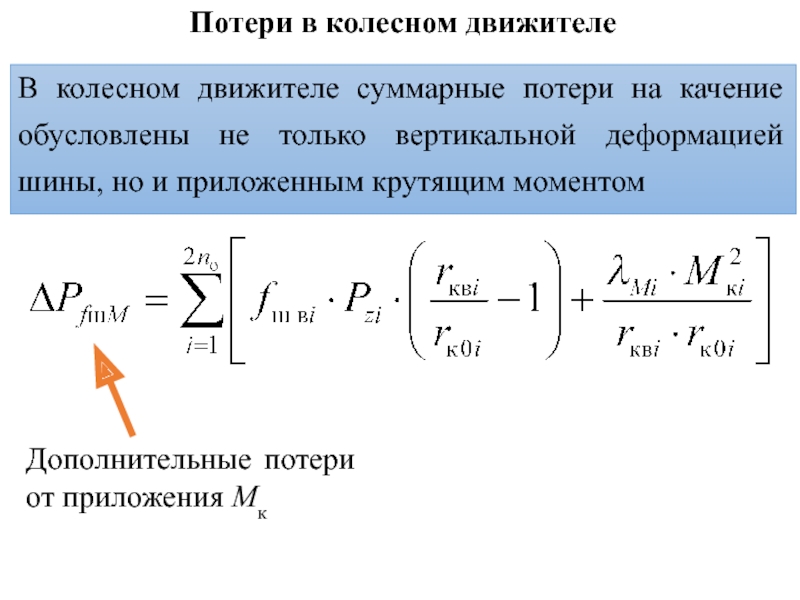
В колесном движителе суммарные потери на качение
обусловлены не только вертикальной деформацией шины, но и приложенным крутящим
моментом
Дополнительные потери от приложения Mк
Слайд 22Потери в колесном движителе
Если рассматривать многоосную КМ с числом осей
nо, у которых ведущая сила одинакова, то получим, что для
преодоления одного и того же внешнего сопротивления (при отсутствии непосредственного скольжения) затраты энергии будут больше у КМ с одной ведущей осью.
Это справедливо для КМ с полностью дифференциальным приводом, при блокированной связи это правило не всегда выполняется.
Слайд 23Тяговые возможности КМ определяются суммарными продольными реакциями на колесах.
Реакции зависят
от Mк:
Момент на колесе, реализуемый по условиям сцепления равен:
Слайд 24При полностью дифференциальной схеме трансмиссии (Mкi = const) на всех
КД одинаковая окружная сила:
Mкi = 0, если Rzi = 0
или φ = 0, тогда установившееся движение невозможно.
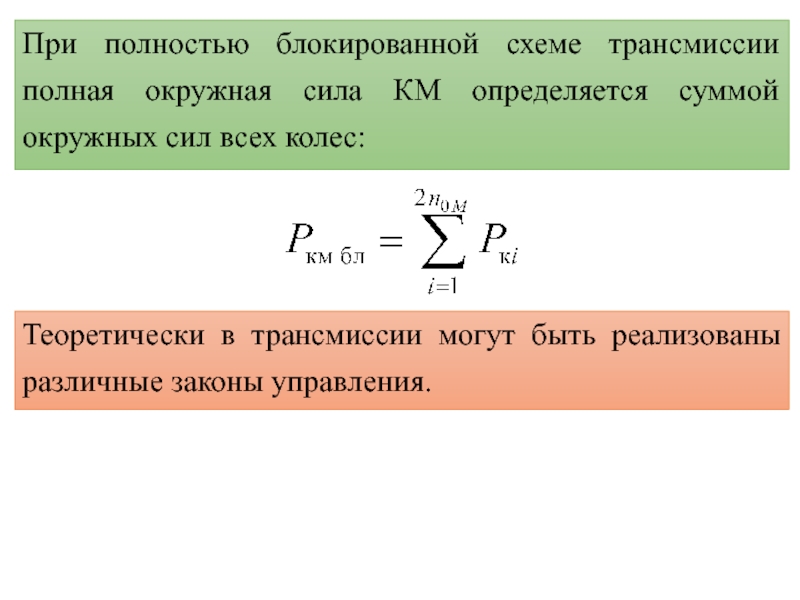
Слайд 25При полностью блокированной схеме трансмиссии полная окружная сила КМ определяется
суммой окружных сил всех колес:
Теоретически в трансмиссии могут быть реализованы
различные законы управления.
Слайд 26Наиболее простые законы управления (постоянство параметров):
Блокированная (ωкi = const)
Дифференциальная (Mкi
= const)
Постоянство мощности на колесах (Nкi = const)
Общего скольжения (Sбкi
= const)
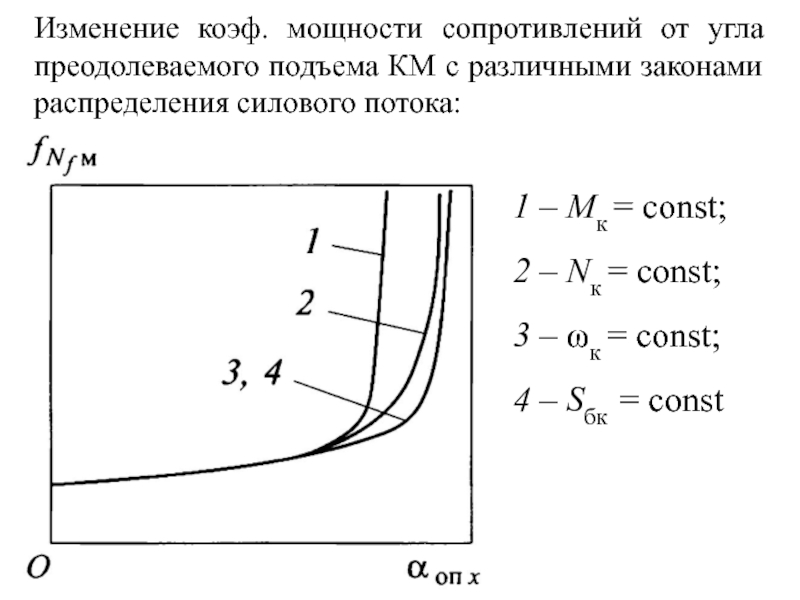
Слайд 27Изменение коэф. мощности сопротивлений от угла преодолеваемого подъема КМ с
различными законами распределения силового потока:
1 – Мк = const;
2
– Nк = const;
3 – к = const;
4 – Sбк = const