Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление интегралов методом М-К
Содержание
- 1. Вычисление интегралов методом М-К
- 2. Обнинский Институт Атомной ЭнергетикиМОДЕЛИРОВАНИЕИНФОРМАЦИОННЫХСИСТЕМГулина Ольга Михайловнаolga@iate.obninsk.ruСopyright © 2001 by Nataly PashkovaE-mail: natik_pna@mail.ru
- 3. Вычисление интегралов методом Монте-Карло
- 4. Метод Монте-КарлоZ=g(ξ),
- 5. Общий метод оценки математических ожиданий
- 6. Оценка эмпирической дисперсии
- 7. Общий метод оценки математических ожиданий
- 8. Вычисление интегралов методом Монте-Карло
- 9. Алгоритм вычисления интеграла
- 10. Простейший метод Монте-Карло I=p1(P)=1/SG при P∈G f1(P)=SG*f(P)
- 11. Трудоемкость алгоритма Монте-Карлоt*Dξ
- 12. Способы уменьшения дисперсии
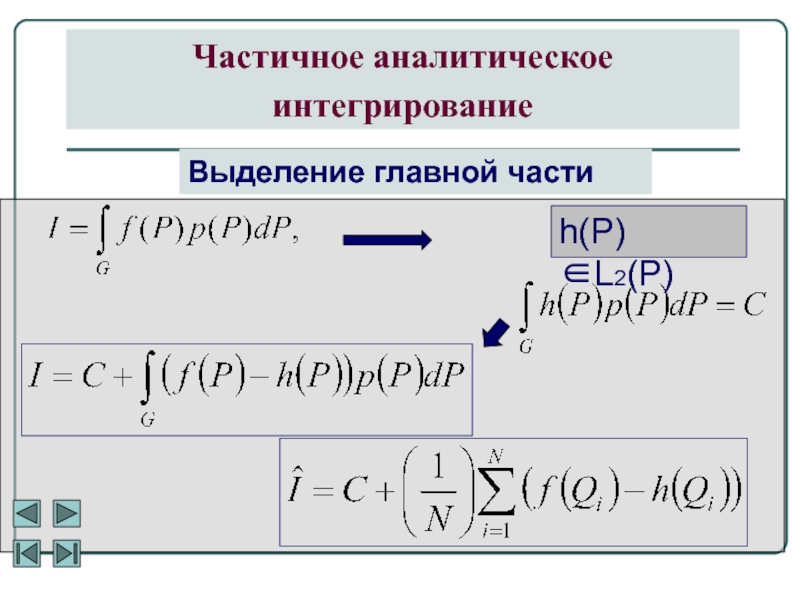
- 13. Частичное аналитическое интегрирование Выделение главной частиh(P)∈L2(P)
- 14. Частичное аналитическое интегрированиеВыделение главной частиесли,то и DZ
- 15. Частичное аналитическое интегрированиеИнтегрирование по части области где 0
- 16. Частичное аналитическое интегрированиеИнтегрирование по части области В G1 p1(P)=p(P)/(1-c)DZ`
- 17. 2 Метод существенной выборкиПлотность p(P), определенную в
- 18. Метод существенной выборки
- 19. Теорема. Минимальная дисперсия DZ0 реализуется в случае, когда плотность p(P) пропорциональна |f(P)|, и равнаМетод существенной выборки
- 20. Метод существенной выборкиМетод предложен Г. Каном и называется методом существенной выборки (importance sampling)
- 21. Метод существенной выборки
- 22. Скачать презентанцию
Обнинский Институт Атомной ЭнергетикиМОДЕЛИРОВАНИЕИНФОРМАЦИОННЫХСИСТЕМГулина Ольга Михайловнаolga@iate.obninsk.ruСopyright © 2001 by Nataly PashkovaE-mail: natik_pna@mail.ru
Слайды и текст этой презентации
Слайд 2Обнинский Институт Атомной Энергетики
МОДЕЛИРОВАНИЕ
ИНФОРМАЦИОННЫХ
СИСТЕМ
Гулина Ольга Михайловна
olga@iate.obninsk.ru
Сopyright © 2001 by Nataly
Pashkova
Слайд 16Частичное аналитическое интегрирование
Интегрирование по части области
В G1
p1(P)=p(P)/(1-c)
DZ`
Слайд 172 Метод существенной выборки
Плотность p(P), определенную в G, назовем допустимой
по отношению к f(P), если p(P)>0 в тех точках, где
f(P)≠0.
Слайд 19Теорема. Минимальная дисперсия DZ0 реализуется в случае, когда плотность p(P)
пропорциональна |f(P)|, и равна
Метод существенной выборки
Слайд 20Метод существенной выборки
Метод предложен Г. Каном и называется методом существенной
выборки (importance sampling)
