Вычислительная математика — это наука о методах решения математических задач на

на компьютере.
Задачами вычислительной математики занимались:

Эйлер,
Лагранж,
Чебышёв,
Якоби,
Лежандр,
фон

Нейман,
...

Вычислительная математика – прикладная математика – численные методы

движения небесных светил. Они много сделали для развития вычислительной математики. Вершиной

достижений в математике считают исследования знаменитого александрийского математика и астронома Клавдия Птолемея. Он жил в первой половине II века н. э. и оставил после себя сочинения в тринадцати томах под названием «Великое собрание, или Великое построение».

первых таблиц логарифмов - шотландский математик Джон Непер и швейцарский

ученый Йоост Бюрги.
Выдающееся значение работ Непера в том, что он раскрыл сущность логарифма как новой, до него неизвестной математической зависимости. Ее открытие имело для вычислительной математики столь же большое значение, как открытие тригонометрических функций.

3) Для расчета динамических процессов нужны математические методы дифференциального и интегрального исчисления науки об изменяющихся величинах. Ее создали гениальные математики Лейбниц, Ньютон, Эйлер и их ученики и последователи.

-достоверность;
-объективность;
- …

недостатки:
- дорого;
- медленно;
- опасно;
- невозможно

Математическое моделирование

Реальное
явление

Математическая
модель

схематизация

Мат. модель обычно состоит из
Уравнений (алгебр., дифференц.,
интеграль. и пр.).
В эти уравнения в качестве
параметров и коэффициентов
могут входить свойства и
характеристики тел, веществ, …

численные
докомпьют. период
компьютер
Аналитические методы
Класс. математика
Приближенные методы
- разложение в

ряды;
- разложение по малому параметру;
- . . .

л о в

е к

Математическая модель должна быть доведена до алгоритма,
сводящего все вычисления к арифметическим и логическим действиям.

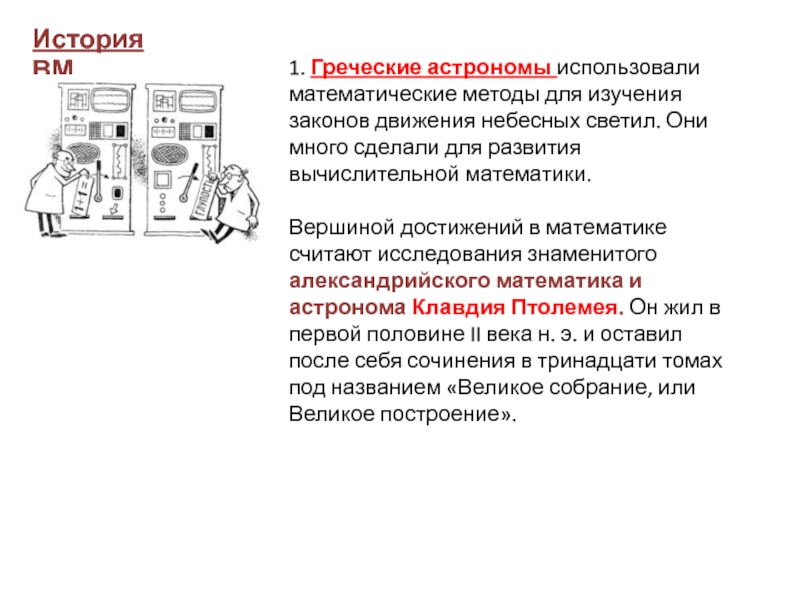
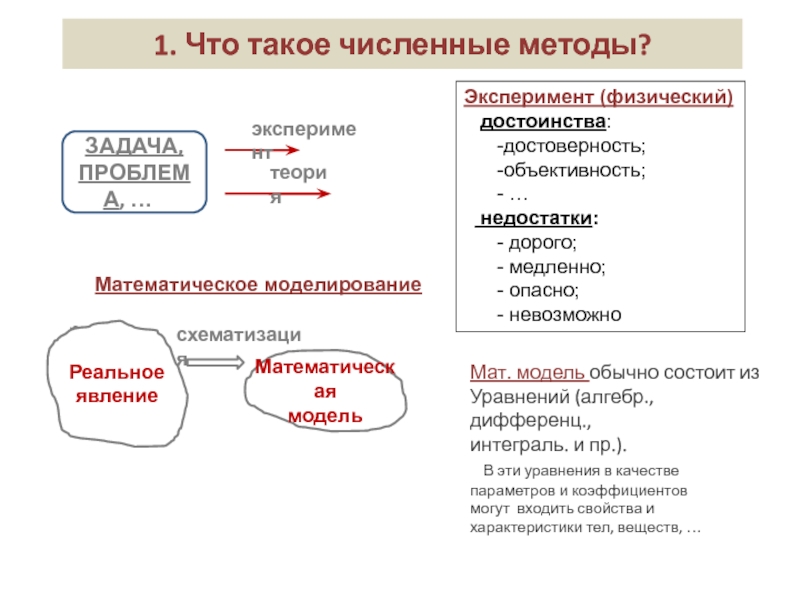
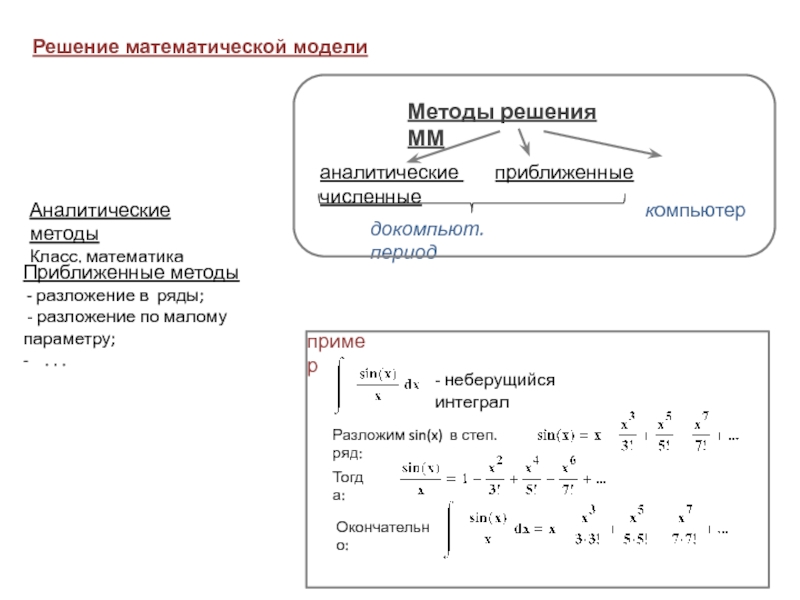
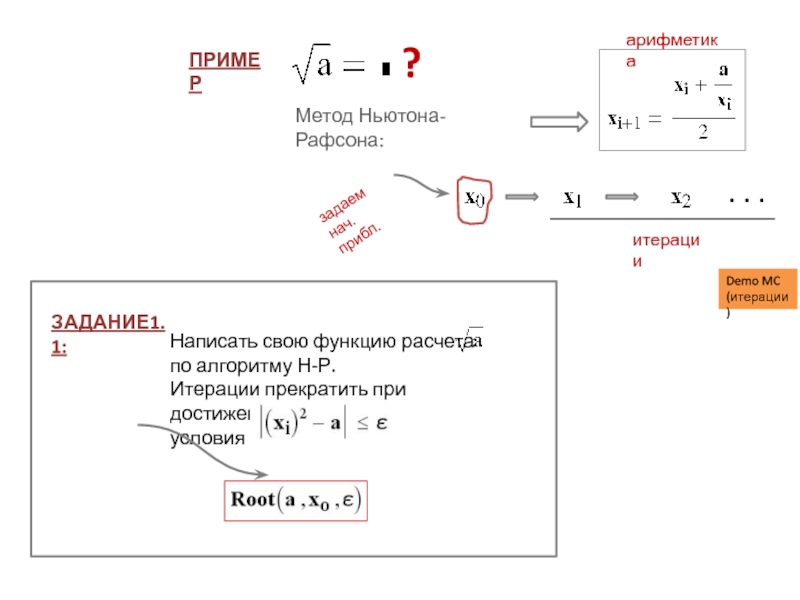
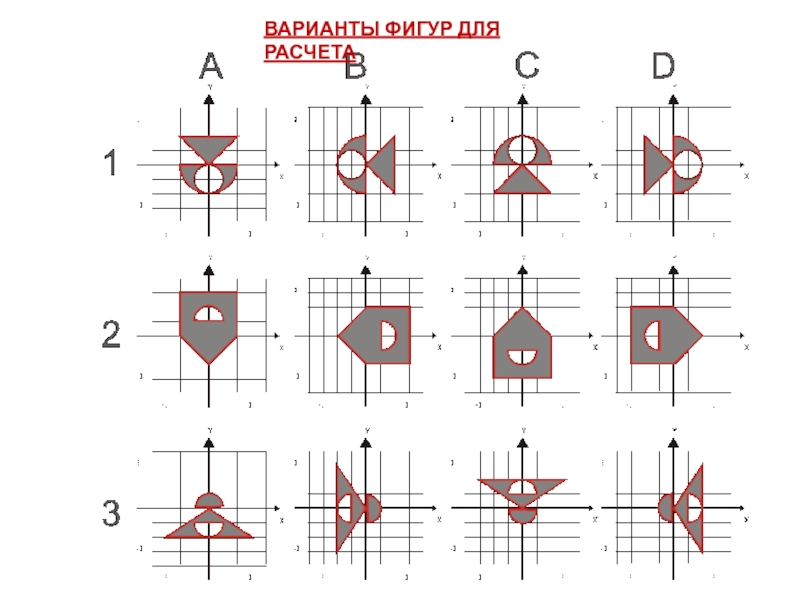
рассчитать ее площадь S.

Опишем вокруг заданной фигуры прямоугольник, его площадь

SS легко можно рассчитать.

В полученный прямоугольник будем случайным образом помещать точки с координатами (x,y). Часть таких точек попадет во внутрь исследуемой фигуры, другая часть окажется за ее пределами.

Обозначим через NN общее количество точек, N – количество точек, попавших в фигуру. Тогда можно записать приближенное равенство

Таким образом, используемый метод является приближенным. Точность расчета существенно зависит от количества заданных случайных точек и качества генератора случайных чисел. Для нашей задачи рекомендуется задавать NN>10000.
(пример на MC – число pi)

ЗАДАНИЕ1.2: Используя метод МК,
найти площадь заданной
фигуры.

(см. ниже)

Demo MC
(pi М-Карло)