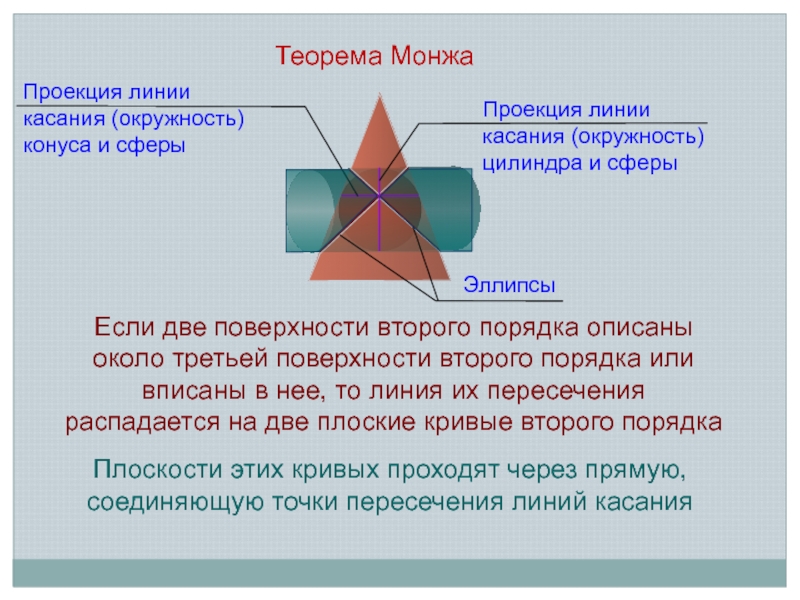
на две отдельные кривые
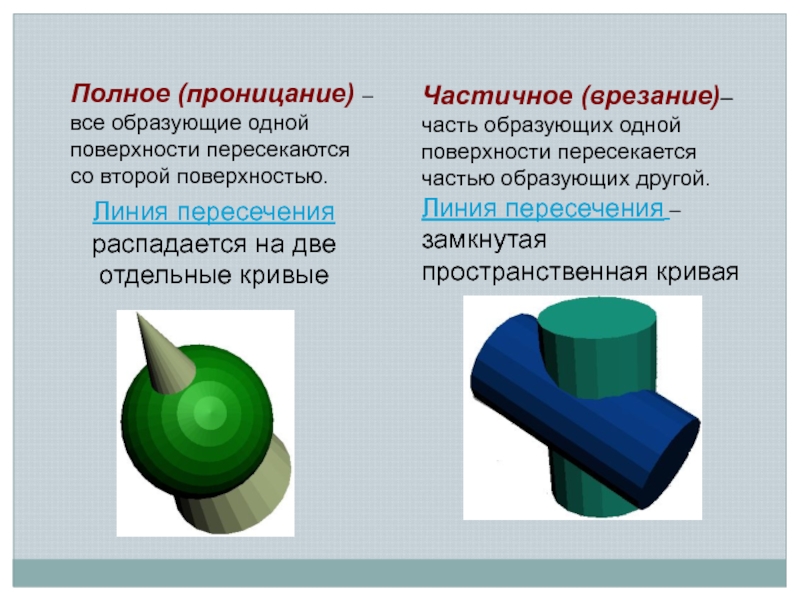
Полное (проницание) – все образующие одной поверхности
пересекаются со второй поверхностью. Частичное (врезание)– часть образующих одной поверхности пересекается частью образующих другой. Линия пересечения –замкнутая пространственная кривая