Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Южный федеральный университет Кафедра синергетики и процессов
Содержание
- 1. Южный федеральный университет Кафедра синергетики и процессов
- 2. Не менее 70% реальных задач математического программирования,
- 3. 1.1 Основные понятия и определения Граф (сеть)
- 4. Ориентированный цикл - это цикл, в котором
- 5. 1.2 Алгоритм построения минимального остовного дереваАлгоритм построения
- 6. Слайд 6
- 7. Пример 1. Телевизионная компания планирует подключение к
- 8. Основные этапы. 2. Примем k=2.
- 9. Основные этапы. 3. Примем k=3. Ищем
- 10. Основные этапы. 4. Примем k=4. Ищем
- 11. Основные этапы. 5. Примем k=5. Ищем
- 12. Альтернативные ребра(но реализовано может быть только одно
- 13. 2. Задание для самостоятельной работы2.1. Решить задачу
- 14. Скачать презентанцию
Не менее 70% реальных задач математического программирования, составляющих большинство задач системного анализа, можно представить в виде сетевых моделей.Построение минимального остовного дерева в задачах принятия решения
Слайды и текст этой презентации
Слайд 1Южный федеральный университет
Кафедра синергетики и процессов управления
Презентация
к практическому занятию
№1 по дисциплине
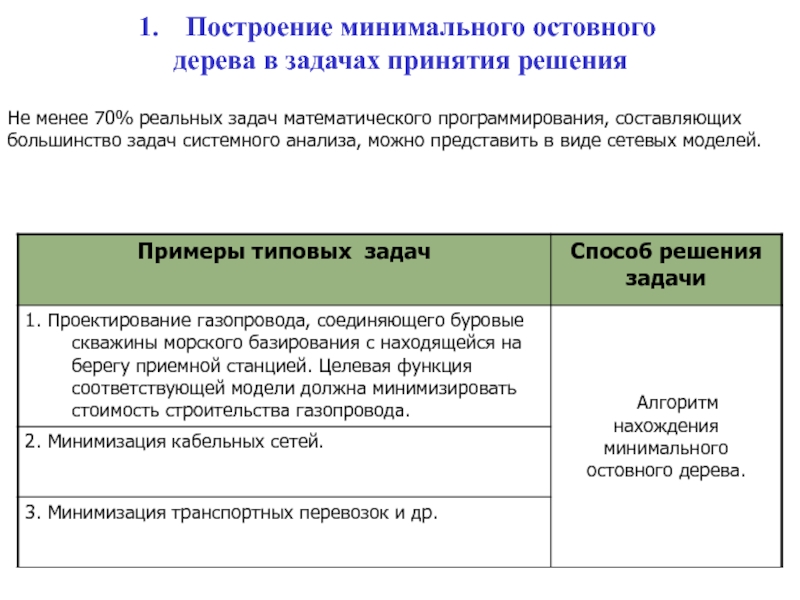
«Системный анализ и управление»
Слайд 2Не менее 70% реальных задач математического программирования, составляющих большинство задач
системного анализа, можно представить в виде сетевых моделей.
Построение минимального остовного
дерева в задачах принятия решения
Слайд 31.1 Основные понятия и определения
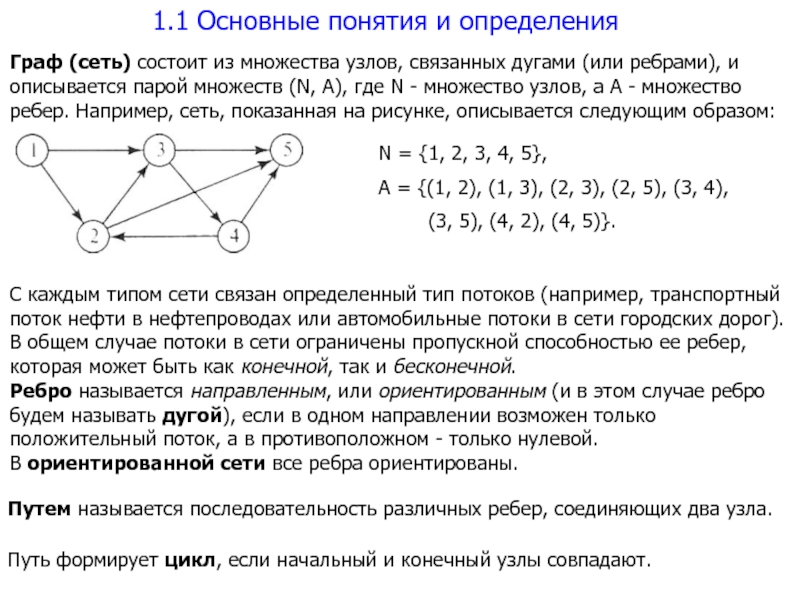
Граф (сеть) состоит из множества
узлов, связанных дугами (или ребрами), и описывается парой множеств (N,
А), где N - множество узлов, а А - множество ребер. Например, сеть, показанная на рисунке, описывается следующим образом:N = {1, 2, 3, 4, 5},
А = {(1, 2), (1, 3), (2, 3), (2, 5), (3, 4),
(3, 5), (4, 2), (4, 5)}.
С каждым типом сети связан определенный тип потоков (например, транспортный поток нефти в нефтепроводах или автомобильные потоки в сети городских дорог). В общем случае потоки в сети ограничены пропускной способностью ее ребер, которая может быть как конечной, так и бесконечной.
Ребро называется направленным, или ориентированным (и в этом случае ребро будем называть дугой), если в одном направлении возможен только положительный поток, а в противоположном - только нулевой.
В ориентированной сети все ребра ориентированы.
Путем называется последовательность различных ребер, соединяющих два узла.
Путь формирует цикл, если начальный и конечный узлы совпадают.
Слайд 4Ориентированный цикл - это цикл, в котором все дуги ориентированы
в определенном направлении.
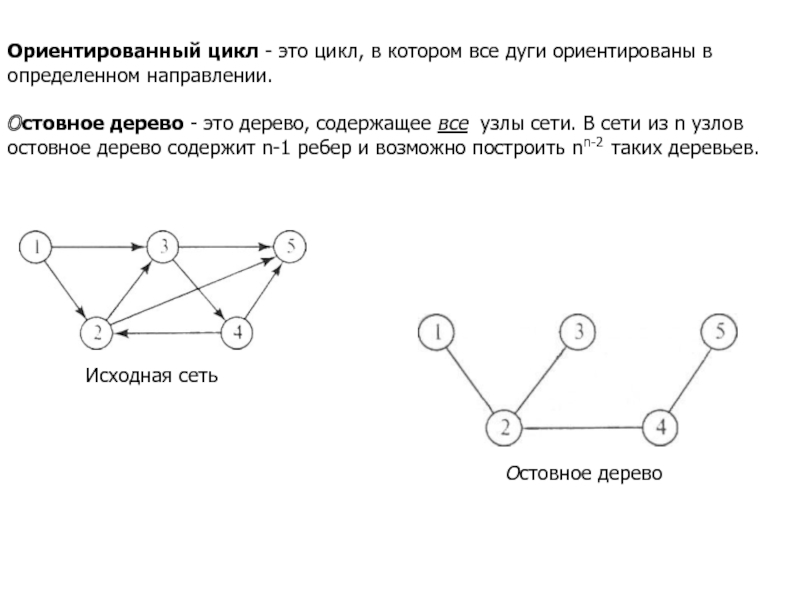
Остовное дерево - это дерево, содержащее все узлы
сети. В сети из n узлов остовное дерево содержит n-1 ребер и возможно построить nn-2 таких деревьев.Исходная сеть
Остовное дерево
Слайд 51.2 Алгоритм построения минимального остовного дерева
Алгоритм построения минимального остовного дерева
предполагает соединение всех узлов сети с помощью путей наименьшей длины.
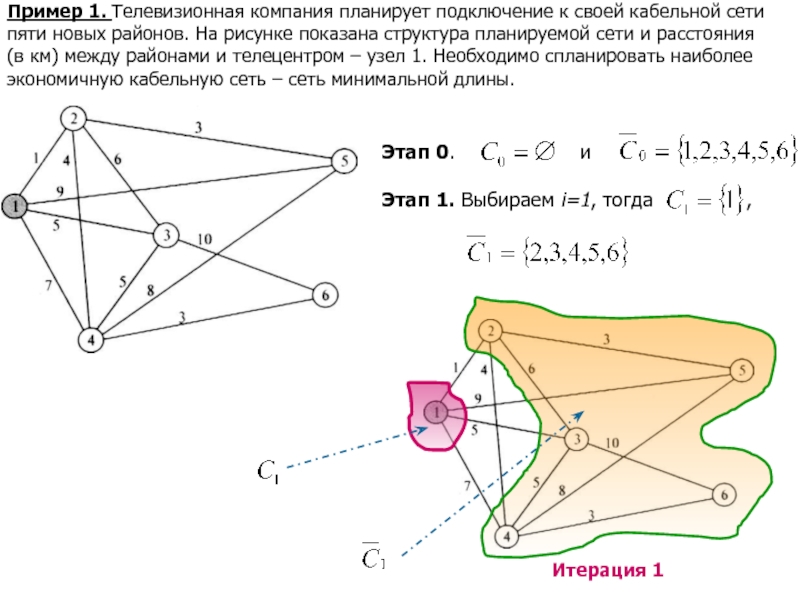
Слайд 7Пример 1. Телевизионная компания планирует подключение к своей кабельной сети
пяти новых районов. На рисунке показана структура планируемой сети и
расстояния (в км) между районами и телецентром – узел 1. Необходимо спланировать наиболее экономичную кабельную сеть – сеть минимальной длины.Этап 0. и
Этап 1. Выбираем i=1, тогда ,
Итерация 1
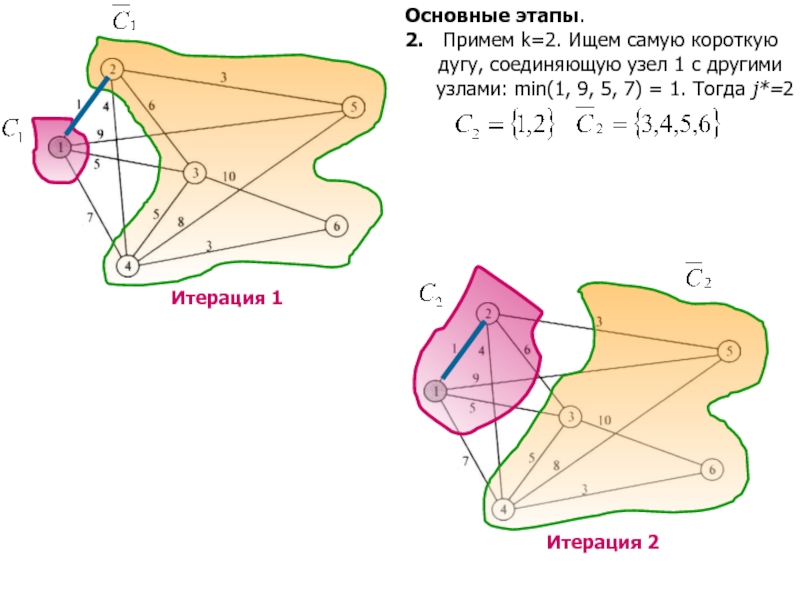
Слайд 8Основные этапы.
2. Примем k=2. Ищем самую короткую
дугу,
соединяющую узел 1 с другими
узлами: min(1,
9, 5, 7) = 1. Тогда j*=2 
Слайд 9Основные этапы.
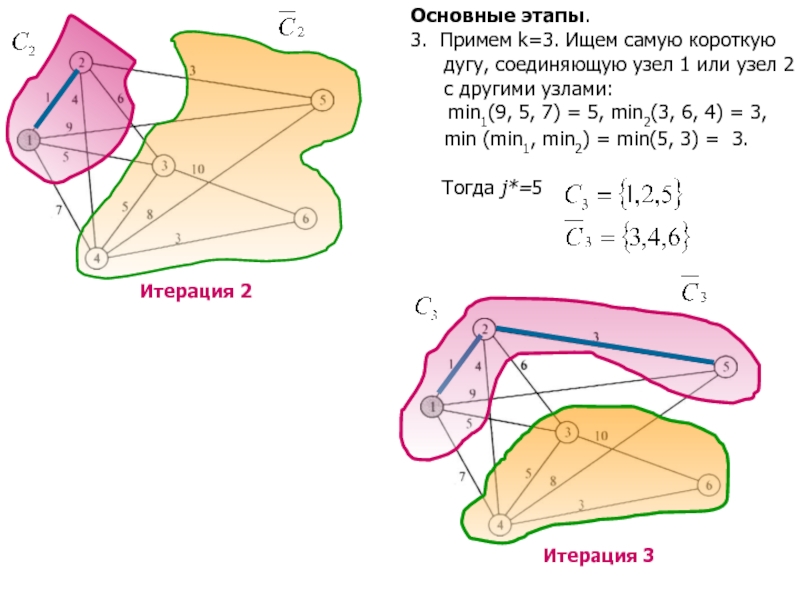
3. Примем k=3. Ищем самую короткую
дугу, соединяющую
узел 1 или узел 2
с другими узлами:
min1(9, 5, 7) = 5, min2(3, 6, 4) = 3,
min (min1, min2) = min(5, 3) = 3. Тогда j*=5
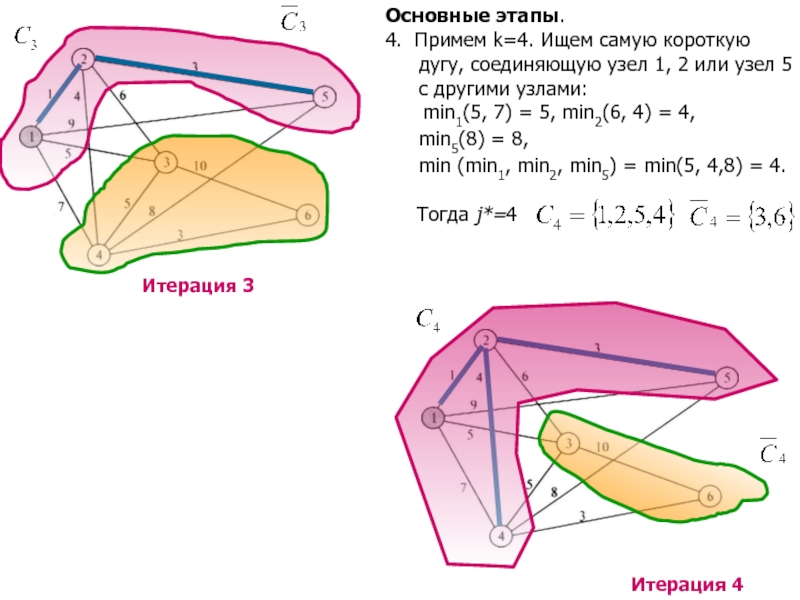
Слайд 10Основные этапы.
4. Примем k=4. Ищем самую короткую
дугу, соединяющую
узел 1, 2 или узел 5
с другими узлами:
min1(5, 7) = 5, min2(6, 4) = 4,
min5(8) = 8,
min (min1, min2, min5) = min(5, 4,8) = 4. Тогда j*=4
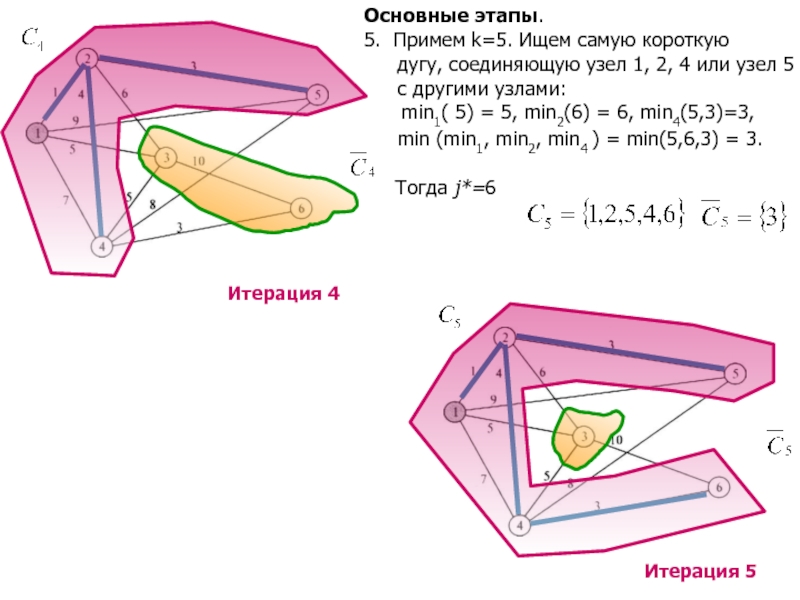
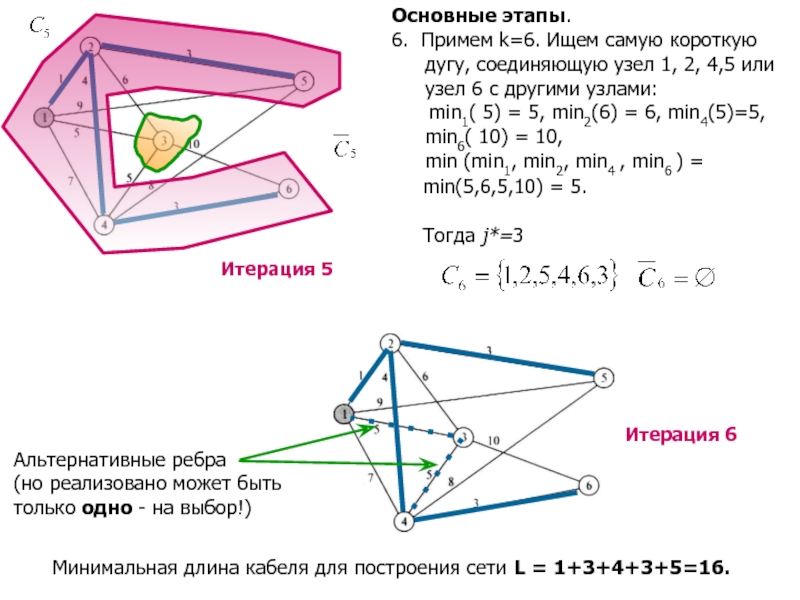
Слайд 11Основные этапы.
5. Примем k=5. Ищем самую короткую
дугу, соединяющую
узел 1, 2, 4 или узел 5
с другими узлами:
min1( 5) = 5, min2(6) = 6, min4(5,3)=3,
min (min1, min2, min4 ) = min(5,6,3) = 3. Тогда j*=6
Слайд 12Альтернативные ребра
(но реализовано может быть
только одно - на выбор!)
Минимальная длина
кабеля для построения сети L = 1+3+4+3+5=16.
Слайд 132. Задание для самостоятельной работы
2.1. Решить задачу из Примера 1
при следующих условиях:
а) узлы 1 и 2 связаны кабелем длиной
8 км;б) узлы 3 и 5 связаны кабелем длиной 2 км;
в) узлы 2 и 6 связаны кабелем длиной 4 км;
г) узлы 5 и 6 связаны кабелем длиной 2 км;
д) узлы 2 и 5 не связаны.
