Задачи на переливание

Содержание

1. Задачи на переливание
2. Задачи на переливание – это задачи, в
3. Разминка задача 1Отмерить 3 л, имея сосуд
4. Решение:1.Наливаем в кастрюлю 4литра. 2.Переливаем воду из
5. Способ перебора возможных вариантов не совсем
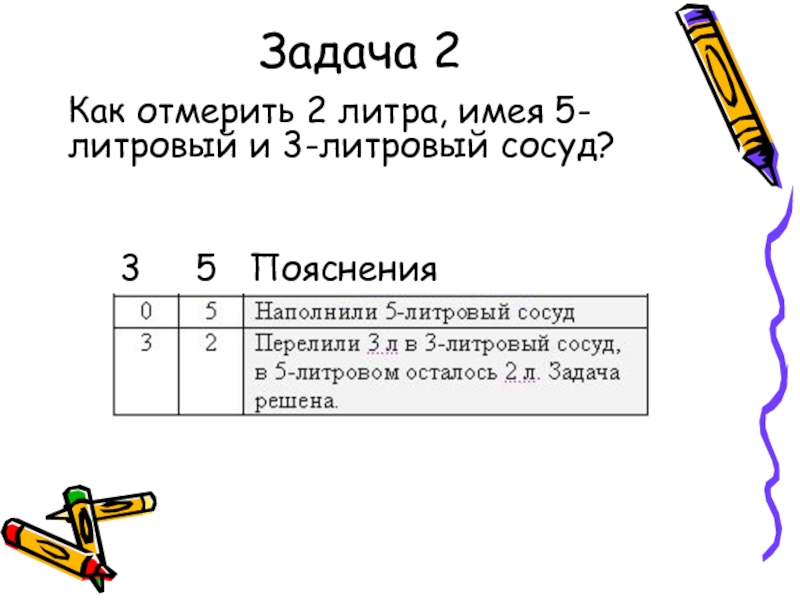
6. Задача 2Как отмерить 2 литра, имея 5-литровый
7. задача 3Бэтмен и Человек-Паук никак не
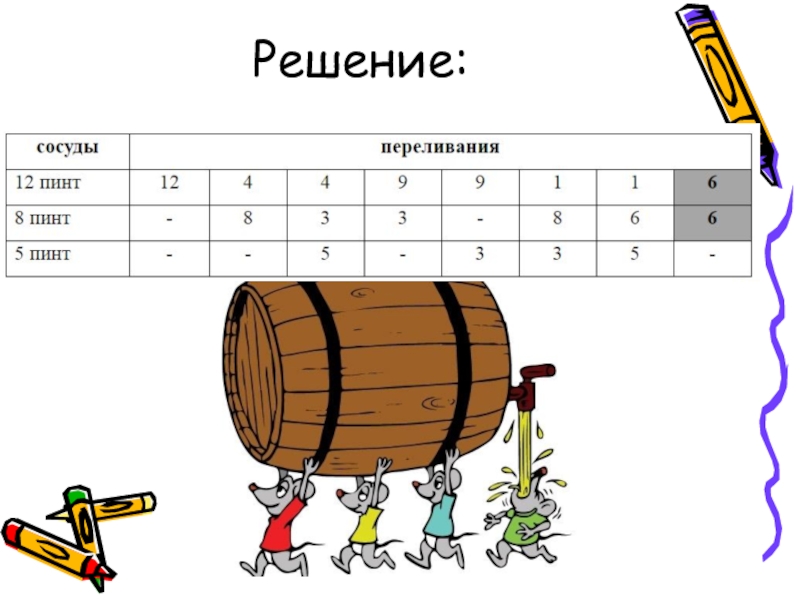
8. Решение:
9. Задача4Дядя Федор собрался ехать к родителям в
10. Решение:
11. Задача 5Для приготовления компота маме нужно налить
12. Решение.Нальём в 3-литровую банку воду и перельём
13. (задача 6Пуассона) Известному французскому математику Симону Пуассону(1981-1840)
14. Решение:
15. Задача 7 Есть два ведра: одно ёмкостью
16. Решение:
17. Задача 8а) Можно ли, имея две банки
18. Решение:
19. Решение:б) Ответ: нельзя.Решение. Так как и
20. Задача 9Отлейте из цистерны 13 литров воды, пользуясь бидонами в 5 л и 17 л.
21. Решение:
22. Задача 10Можно ли набрать из реки 8
23. Решение:
24. Задача 11Есть три кастрюли: 8 л −
25. Решение:
26. Задача 12Можно ли разлить 50 литров бензина
27. Решение:Если бы это было возможно, то
28. Задача 13 Есть двое песочных часов: на
29. Решение:Переворачиваем и те, и другие часы.
30. Задача 14 Есть две одинаковые чашки: одна
31. Ответ: одинаково.Решение. Во время второго переливания
32. Задача 15 Есть три сосуда 3л, 4л
33. Решение:
34. Спасибо за внимание
35. Скачать презентанцию

Задачи на переливание – это задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости. Простейший прием решения задач этого класса состоит в переборе возможных вариантов.

Главная
Разное
Задачи на переливание

Слайды и текст этой презентации

Слайд 1Задачи на переливание

Слайд 2Задачи на переливание – это задачи, в которых с помощью

сосудов известных емкостей требуется отмерить некоторое количество жидкости. Простейший прием

решения задач этого класса состоит в переборе возможных вариантов.

Задачи на переливание – это задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество

Слайд 3Разминка задача 1
Отмерить 3 л, имея сосуд 5 л. Можно ли

в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить

3 литра воды?

Разминка задача 1Отмерить 3 л, имея сосуд 5 л. Можно ли в четырехлитровую кастрюлю с помощью крана

Слайд 4Решение:1.Наливаем в кастрюлю 4литра. 2.Переливаем воду из кастрюли в банку.

3.Наливаем в кастрюлю 4 литра. 3.Доливаем полную банку, и в

кастрюле
остается 3 литра

Решение:1.Наливаем в кастрюлю 4литра. 2.Переливаем воду из кастрюли в банку. 3.Наливаем в кастрюлю 4 литра. 3.Доливаем полную

Слайд 5 Способ перебора возможных вариантов не совсем удачный, в нем

трудно выделить какой-либо общий подход к решению других подобных задач.

Более систематический подход к решению задач "на переливание" заключается в использовании отдельных таблиц, в которые заносят количество жидкости в каждом из имеющихся сосудов.

Способ перебора возможных вариантов не совсем удачный, в нем трудно выделить какой-либо общий подход к решению

Слайд 6Задача 2
Как отмерить 2 литра, имея 5-литровый и 3-литровый сосуд?

3 5 Пояснения

Задача 2Как отмерить 2 литра, имея 5-литровый и 3-литровый сосуд? 3 5

Слайд 7 задача 3
Бэтмен и Человек-Паук никак не могли определить, кто

из них главный супергерой. Так и не разрешив свой спор,

отправились они к мудрецу. Он подумал и сказал: «Самый главный супергерой – это не тот, кто сильнее, а тот, кто сообразительнее! Вот, кто решит задачу, тот и будет самым-самым! Имеются два сосуда вместимостью 8 л и 5 л.
Как с помощью этих
сосудов налить из источника
7л воды?

задача 3Бэтмен и Человек-Паук никак не могли определить, кто из них главный супергерой. Так и не

Слайд 8Решение:

Слайд 9Задача4
Дядя Федор собрался ехать к родителям в гости и попросил

у кота Матроскина 4 л простоквашинского молока. А у Матроскина

только 2 пустых бидона: трехлитровый и пятилитровый. И восьмилитровое ведро, наполненное молоком.
Как Матроскину отлить 4 литра
молока с
помощью имеющихся сосудов?

Задача4Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока.

Слайд 10Решение:

Слайд 11Задача 5
Для приготовления компота маме нужно налить в 5-литровую кастрюли

4 литра воды. Как маме справиться с этой задачей, если

у мамы есть кроме этой кастрюли ещё 3-литровая банка, водопроводный кран и раковина, куда можно выливать воду?

Задача 5Для приготовления компота маме нужно налить в 5-литровую кастрюли 4 литра воды. Как маме справиться с

Слайд 12Решение.
Нальём в 3-литровую банку воду и перельём её в кастрюлю.

Затем еще раз наполним банку и выльём в кастрюлю, сколько

поместится. Тогда в кастрюле будет 5 литров и 1 литр в 3-литровой банке. Теперь выльем всю воду из кастрюли в раковину. Затем перельем литр из банки в кастрюлю и добавим ещё три литра, наполнив банку ещё раз. Теперь в кастрюле 1 + 3 = 4 литра, что и требовалось. Задача решена.

Решение.Нальём в 3-литровую банку воду и перельём её в кастрюлю. Затем еще раз наполним банку и выльём

Слайд 13(задача 6Пуассона) Известному французскому математику Симону Пуассону(1981-1840) в юности предложили

задачу. Заинтересовавшись ею, Пуассон затем увлекся математикой и посвятил этой

науке всю свою жизнь. Вот эта задача. Некто имеет 12 пинт вина и хочет отлить из этого количества половину, но у него нет сосуда в 6 пинт. Зато есть два других сосуда: в 8 пинт и 5 пинт. Спрашивается: каким образом налить 6 пинт в сосуд на 8 пинт?

(задача 6Пуассона) Известному французскому математику Симону Пуассону(1981-1840) в юности предложили задачу. Заинтересовавшись ею, Пуассон затем увлекся математикой

Слайд 14Решение:

Слайд 15Задача 7
Есть два ведра: одно ёмкостью 4 л, другое

− 9 л. Можно ли только с их помощью набрать

из реки ровно 6 литров воды?

Задача 7 Есть два ведра: одно ёмкостью 4 л, другое − 9 л. Можно ли только с

Слайд 16 Решение:

Слайд 17Задача 8
а) Можно ли, имея две банки ёмкостью 3 л

и 5 л, набрать из водопроводного крана 4 литра воды?
б)

Тот же вопрос, если есть только банки ёмкостью 6 л и 9 л?

Задача 8а) Можно ли, имея две банки ёмкостью 3 л и 5 л, набрать из водопроводного крана

Слайд 18 Решение:

Слайд 19 Решение:
б) Ответ: нельзя.
Решение. Так как и 6, и 9

делятся на 3, то после любого количества переливаний объём воды

(в литрах) в каждой из банок будет делиться на 3. Но 1 на 3 не делится.

Решение:б) Ответ: нельзя.Решение. Так как и 6, и 9 делятся на 3, то после любого количества

Слайд 20Задача 9
Отлейте из цистерны 13 литров воды, пользуясь бидонами в

5 л и 17 л.

Слайд 21 Решение:

Слайд 22Задача 10
Можно ли набрать из реки 8 литров воды с

помощью двух ведёр, вместимостью 15 л и 16 л?

Задача 10Можно ли набрать из реки 8 литров воды с помощью двух ведёр, вместимостью 15 л и

Слайд 23 Решение:

Слайд 24Задача 11
Есть три кастрюли: 8 л − с компотом, 3

л и 5 л − пустые. Как разделить компот пополам?

(Компот, в отличие от воды, выливать нельзя.)

Задача 11Есть три кастрюли: 8 л − с компотом, 3 л и 5 л − пустые. Как

Слайд 25 Решение:

Слайд 26Задача 12
Можно ли разлить 50 литров бензина по трём бакам

так, чтобы в первом баке было на 10 литров больше,

чем во втором, а во втором на 21 литр больше, чем в третьем?

Задача 12Можно ли разлить 50 литров бензина по трём бакам так, чтобы в первом баке было на

Слайд 27 Решение:

Если бы это было возможно, то во втором баке

должно было бы быть не меньше 21 л бензина (так

как иначе в нём не могло бы быть на 21 литр больше, чем в третьем). Значит, в первом баке должно быть не меньше 31 л, так как в нём на 10 литров больше, чем во втором. Но тогда только в первом и втором должно быть не меньше 21 + 31 = 52 литров. Противоречие.