Задание выполняем письменно все вместе в течение сегодняшних упражнений Будут

задачи и далее задание по идеям проектирования

Листок подписываем сверху и

им. М.В. Ломоносова.

средств?


Возможность реализации в действующих рыночных условиях?


Вопрос о распределении имеющихся в

финансовых потоков
основные способы начисления износа оборудования
методы оценки инвестиций в

вклада лучше всего выбрать? Положить ли деньги в банк или

Проценты – I
Процентная ставка
Исходная инвестированная сумма – Р
Наращенная сумма - S
S = Р + I.
Коэффициент наращения - k
k = S/P.

Период начисления
Интервал начисления

каждого интервала начисления. ставка называется ссудном процентом.

антисипативный (предварительный) способ -

помещена в банк под і процентов годовых (проценты простые).
Прошел 1

Задача 1. Первоначальная сумма Р = 7000 руб. помещена в банк на n = 0,5 года под і = 10% годовых (проценты простые). Найти наращенную сумму

S = 4500 руб., і = 20% годовых (проценты простые).

Задача 2. Первоначальная сумма Р = 6000 руб., наращенная сумма S = 7200 руб., і = 10% годовых (проценты простые). Найти период начисления.

S = 2200 руб., период начисления п = 0,5 года.

Задача 3. Первоначальная сумма Р = 3000 руб., наращенная сумма S = 3300 руб., период начисления п = 0,5 года. Найти простую процентную ставку.

начисления n и простой процентной ставке і нужно определить первоначальную

Пример 4. Наращенная сумма S = 7000 руб., период начисления n = 0,25 года (один квартал), простая процентная ставка і = 12% годовых. Тогда первоначальная сумма

Задача 4. Наращенная сумма S = 6000 руб., период начисления n = 0,5 года, простая процентная ставка і — 15% годовых. Найти первоначальную сумму.

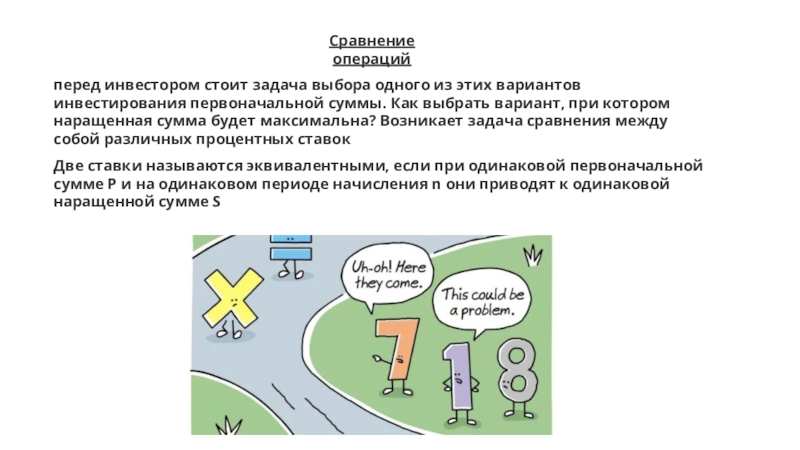
измеряется в годах.

период начисления может быть меньше года =>

В немецкой практике начисления процентов один полный месяц равен 30 дням, продолжительность года К = 360 дней.
Во французской практике период начисления процентов равен фактическому сроку, продолжительность года К = 360 дней.
В английской практике период начисления процентов равен фактическому сроку, продолжительность года К = 365 дней (невисокосный год) или 366 дней (високосный год).

Пример 5. Первоначальная сумма Р = 3000 руб. помещена в банк под і = 12% годовых (проценты простые) на срок с 18 марта 2003 года по 20 октября 2003 года. Найдем наращенную сумму в каждой из практик начисления процентов.

В немецкой практике

t = 14 (март) + 6X30 (апрель, май, июнь, июль, август, сентябрь) + 20 (октябрь) -— 1 (день открытия и день закрытия счета всегда считаются за один день) = 213 дней.

Во французской практике t = 14 (март) + 30 (апрель) + 31 (май) + 30 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 20 (октябрь) - 1 = 216 дней. S = 3000 Х(1 + 0,12X216/360) = 3216 руб.

Задача 5. Первоначальная сумма Р = 2000 руб. помещена в банк под і = 15% годовых (проценты простые) на срок с 19 февраля 2003 года по 27 ноября 2003 года. Найти наращенную сумму по английской практикe начисления процентов

= 3000 руб. В первой половине года применялась простая процентная

Задача 6 Первоначальная сумма Р = 4000 руб. В первой половине года применялась простая процентная ставка i1 = 11% годовых, во второй половине года применялась простая процентная ставка i2 = 14 % годовых. Найти наращенную сумму.

процентов годовых (проценты сложные).
Прошел 1 год.

Пример 7. Первоначальная сумма Р = 5000 руб. помещена в банк на n = 2 года под і = 15% годовых (проценты сложные).

Задача 7. Первоначальная сумма Р = 7000 руб. помещена в банк на n= 3 года под і = 10% годовых (проценты сложные). Найти наращенную сумму.

ставку i, можно определить период начисления n (в годах):
Пример 8.

Задача 8. Первоначальная сумма Р = 6000 руб., наращенная сумма S = 7200 руб., і = 10% годовых (проценты сложные). Найти период начисления.

(в годах), можно определить сложную годовую процентную ставку і
Пример 9

Задача 9. Первоначальная сумма Р = 3000 руб., наращенная сумма S = 4000 руб., период начисления n = 2 года. Найти сложную процентную ставку.

периоду начисления п и сложной процентной ставке і нужно определить

Пример 10. Наращенная сумма S = 7000 руб., период начисления n = 2 года, сложная процентная ставка і = 12% годовых. Тогда первоначальная сумма: 

Задача 10. Наращенная сумма S = 6000 руб., период начисления п = 3 года, сложная процентная ставка і = 15% годовых. Найти первоначальную сумму.

п не является целым числом, то формула S = Р(1

Определение. Целая часть [n] числа n — это наибольшее целое число, не превосходящее n.

Пример 11. [1,6] = 1, [-2,5] = -3, [0,7] = 0, [5] = 5.

Задача 11. Чему равны целые части чисел -3,5 и 2,9?

Определение. Дробная часть {n} числа n — это разность между числом n и его целой частью: {n} = n — [n]. Всегда 0 < {n} < 1

Пример 12. {1,6} = 0,6; {-2,3} = 0,7; {0,7} = 0,7; {5} = 0.

Задача 12. Чему равны дробные части чисел -3,5 и 2,9?

= [n] + {n}
Пример 13. Первоначальная сумма Р =

Задача 13. Первоначальная сумма Р = 8000 руб. помещена в банк на n = 2,25 года под і = 15% годовых (проценты сложные). Найти наращенную сумму двумя способами.

(в годах) применялись разные сложные процентные ставки соответственно
Пример 14. Первоначальная

Задача 14. Первоначальная сумма Р = 4000 руб., n = 3 года применялась сложная процентная ставка i1 = 11% годовых, затем n2 = 2 года применялась сложная процентная ставка i2 = 14% годовых. Найти наращенную сумму.

сложных процентов может происходить несколько раз в году. В этом

Если в году m интервалов начисления, то на каждом из них процентная ставка равна j/m. Тогда наращенная сумма

Пример 15. Первоначальная сумма Р = 7000 руб., период начисления n = 2 года, сложная процентная ставка j = 12% годовых ежеквартально. Найдем наращенную сумму.

Задача 15. Первоначальная сумма Р = 6000 руб., период начисления n = 3 года, сложная процентная ставка j = 12% годовых ежемесячно. Найти наращенную сумму.

Первоначальная сумма P = 7000 руб., период начисления п =

Задача 16. Найти наращенную сумму в задаче 15 при непрерывном начислении процентов. Сравнить с результатом задачи 15.

инвестирования первоначальной суммы. Как выбрать вариант, при котором наращенная сумма

Две ставки называются эквивалентными, если при одинаковой первоначальной сумме Р и на одинаковом периоде начисления n они приводят к одинаковой наращенной сумме S

Какой вариант инвестирования первоначальной суммы на n = 3 года

Задача 17. Какой вариант инвестирования первоначальной суммы на n = 2 года лучше: под простую процентную ставку 17% годовых или под сложную процентную ставку 15,5% годовых?

18. Какой вариант инвестирования первоначальной суммы на n = 3

Задача 18. Какой вариант инвестирования первоначальной суммы на n = 2 года лучше: под простую процентную ставку 19% годовых или под сложную процентную ставку 14% годовых ежемесячно?

ЭФФЕКТИВНАЯ СЛОЖНАЯ ПРОЦЕНТНАЯ СТАВКА
Эта формула определяет эффективную годовую ставку сложных

Пример 19. Найдем эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке i = 10% годовых ежеквартально.

Вместо начисления каждый квартал 2,5% можно один раз в год начислять 10,4%. От этого наращенная сумма не изменится.

Задача 19. Найти эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке i = 12% годовых ежемесячно

20. Найдем годовую номинальную сложную процентную ставку (проценты начисляются каждый

Вместо начисления один раз в год 15% можно начислять каждый месяц 14,1%/12 = 1,175%. От этого наращенная сумма не изменится

Задача 20. Найти годовую номинальную сложную процентную ставку (проценты начисляются каждые полгода), эквивалентную сложной процентной ставке ісл = 20% годовых.