Функции одного порядка. Символ «О-большое»
Эквивалентные функции
Функция, бесконечно малая по
сравнению с другой функцией. Символ «о-малое»Асимптотическое представление функций


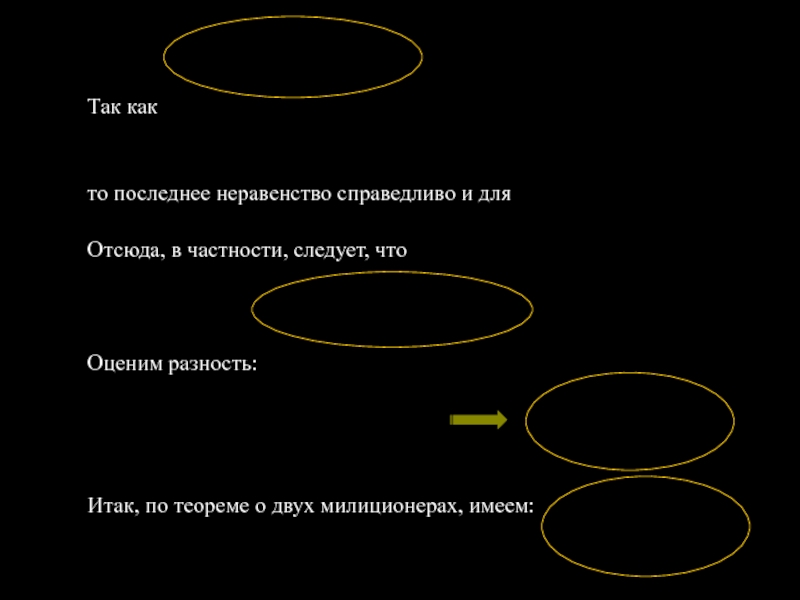
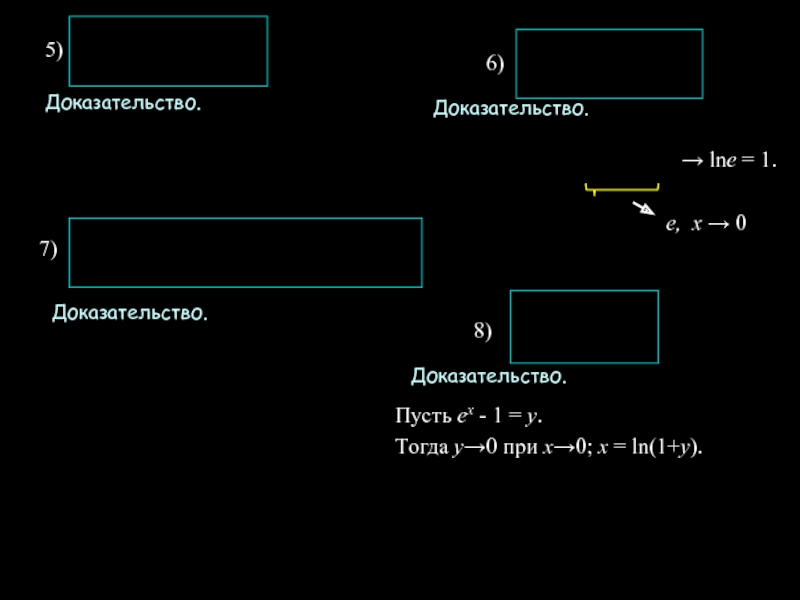
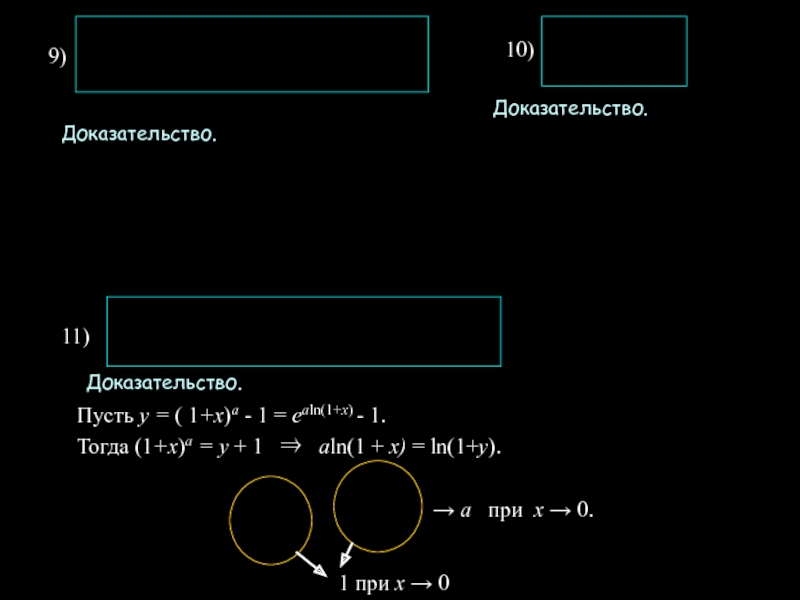
![Замечательные пределы и следствия из них Второй замечательный предел Напомним, что Далее покажем, что Пусть х >1. Положим Второй замечательный предел Напомним, что Далее покажем, что Пусть х >1. Положим n = [х]. Тогда х =](/img/thumbs/2c41d5929161832d350e158819cbe336-800x.jpg)