не меняется (или почти не меняется), так как он не
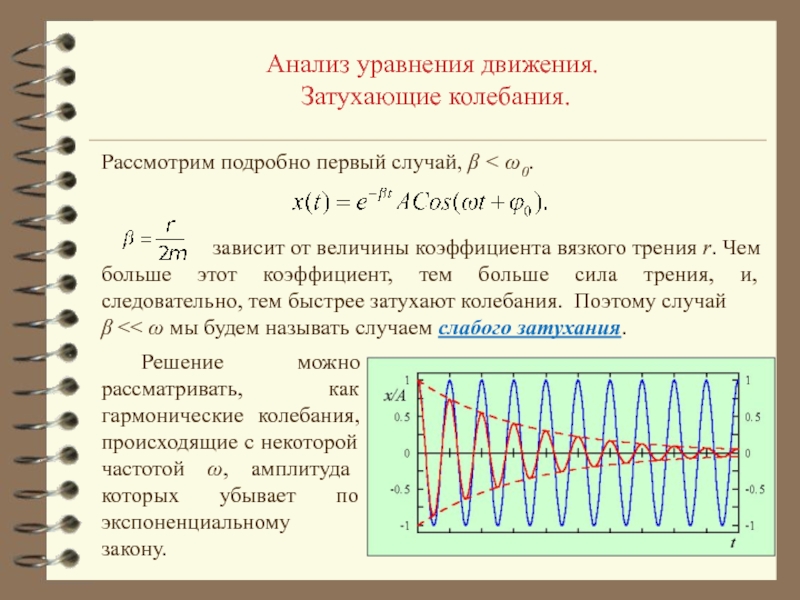
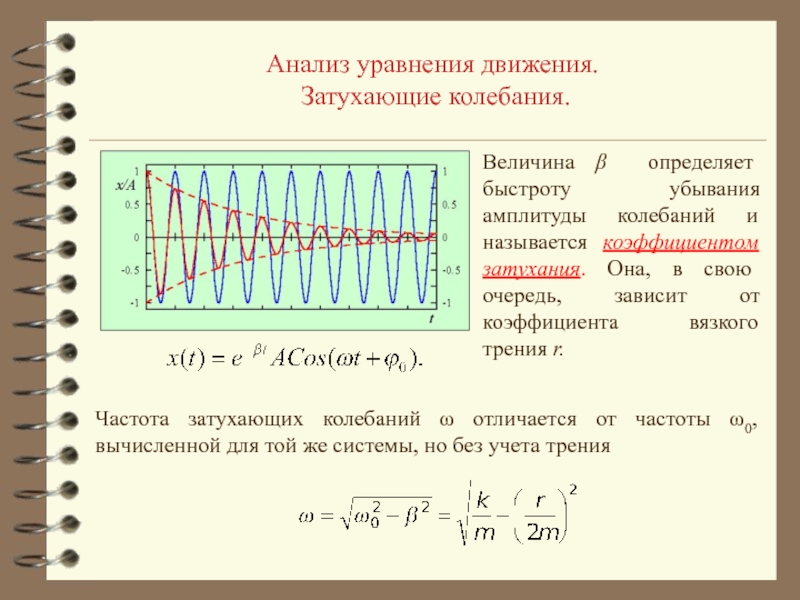
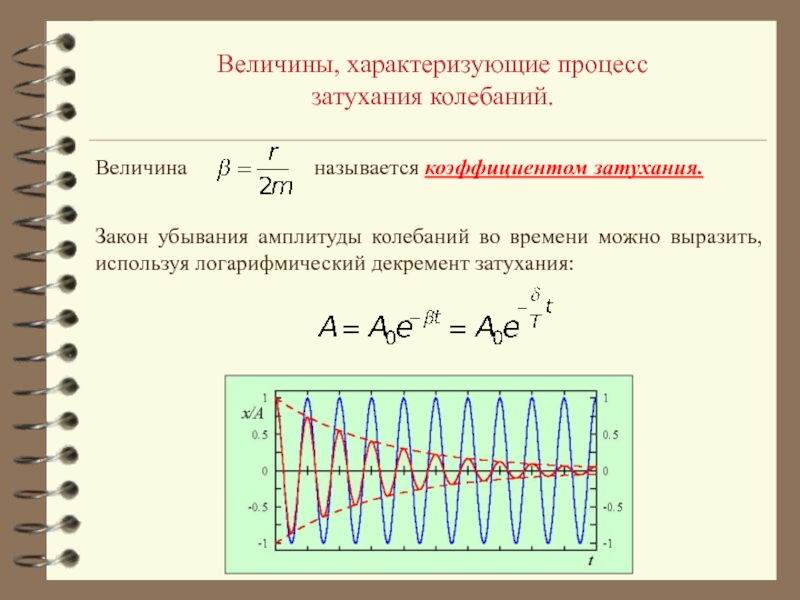
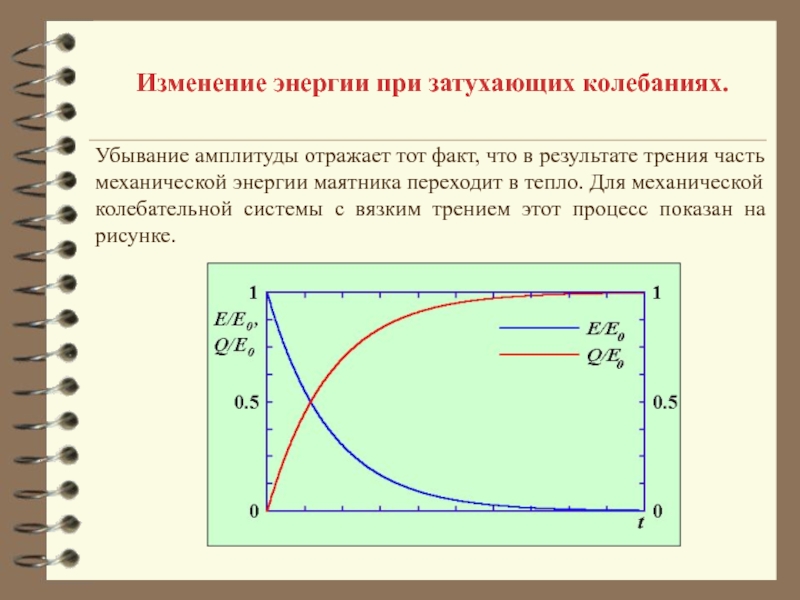
зависит от массы маятника, а, следовательно, от количества высыпавшегося песка.2. Амплитуда колебаний уменьшается с течением времени.
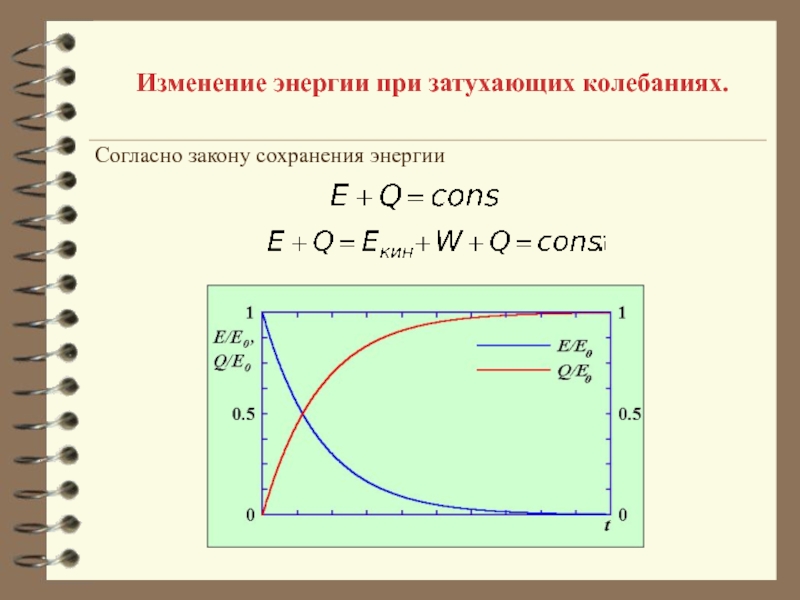
Колебания, амплитуда которых уменьшается с течением времени, называются затухающими колебаниями.