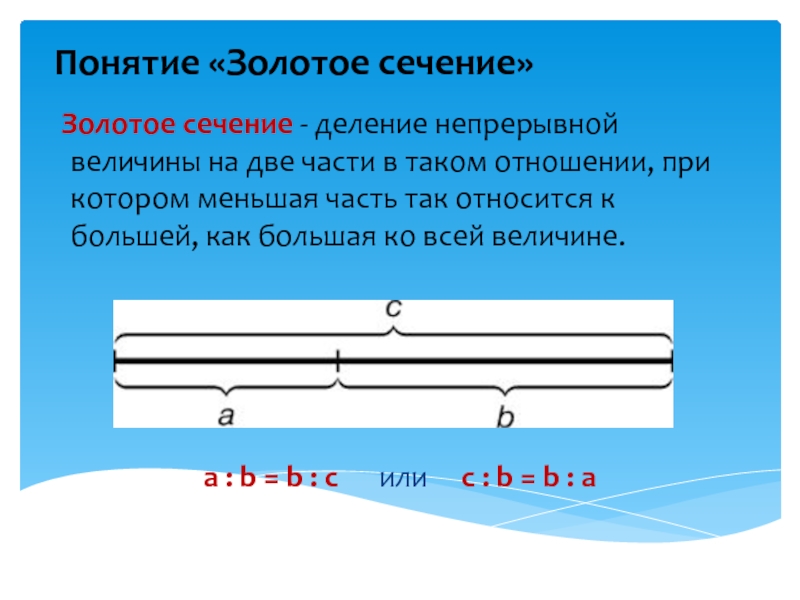
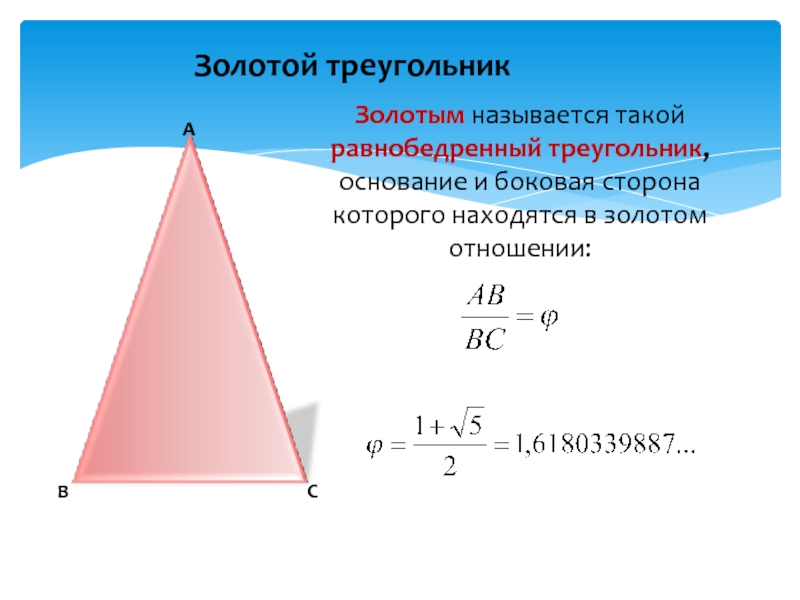
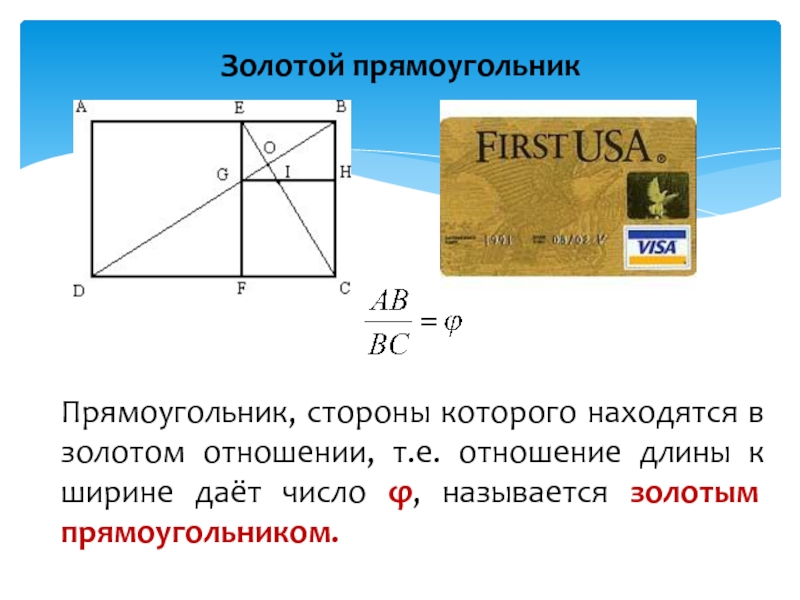
ГОРОДА-КУРОРТА ЖЕЛЕЗНОВОДСКА СТАВРОПОЛЬСКОГО КРАЯ
IX ОТКРЫТАЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ КОНФЕРЕНЦИЯ ШКОЛЬНИКОВ
Секция: Математика
«Золотое
сечение вокруг нас»Выполнил: Черников Евгений,
ученик 7 “б” класса
Научный руководитель: Ермуратина Татьяна Викторовна
учитель математики высшей категории
п.Иноземцево
2013