Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция у = kx?, ее свойства и график
Содержание
- 1. Функция у = kx?, ее свойства и график
- 2. Вспомнить свойства функций у = kx +b
- 3. 06.07.2011Кравченко Г. М.Внимание!Независимая переменная х имеет степени
- 4. 06.07.2011Кравченко Г. М.у = -3х, k =
- 5. у = х², где k = 1;
- 6. у = х², где k = 1;
- 7. Свойства функции y = - kx²у =
- 8. 06.07.2011Кравченко Г. М.Рассмотрим пример 1. Решить графически
- 9. Необходимо построить на одной координатной плоскости графики
- 10. 06.07.2011Кравченко Г. М.Решение Необходимо построить на одной
- 11. Ответить на вопросы:01.07.2011Кравченко Г. М.Назвать свойства функций
- 12. Скачать презентанцию
Вспомнить свойства функций у = kx +b и у = х², их графики.Изучить свойства функции у = kx², у = - kx² и научиться строить график.Научиться по графику определять свойства данных
Слайды и текст этой презентации
Слайд 2Вспомнить свойства функций у = kx +b и у =
х², их графики.
Изучить свойства функции у = kx², у =
- kx² и научиться строить график.Научиться по графику определять свойства данных функций.
Ввести правила решения уравнений графическим способом.
Изучить способ построения графиков функций, заданных несколькими условиями.
Цели:
06.07.2011
Кравченко Г. М.
Слайд 306.07.2011
Кравченко Г. М.
Внимание!
Независимая переменная х имеет степени не выше первой.
Свойства!
График
у = kx + b – прямая.
Свойства зависят от
коэффициента k (определяет наклон графика, при k = 0 прямая параллельна оси абсцисс или совпадает).Точка (o; b) – является точкой пересечения графика с осью ординат.
Слайд 406.07.2011
Кравченко Г. М.
у = -3х,
k = -3, b =
0.
Точки (0; 0), (2; -6).
у = 3х;
k =
3, b = 0.Точки (0; 0), (2; 6).
у = 3х + 4;
k = 3, b = 4.
Точки (0; 4) (-2; -2).
2
6
у = 3х;
4
у = 3х + 4;
у = -3х
-2
-2
-6
3
1
.
.
.
.
.
у = kx + b
Вывод:
график – прямая
K>1, 0 < k < 1, k < 0.
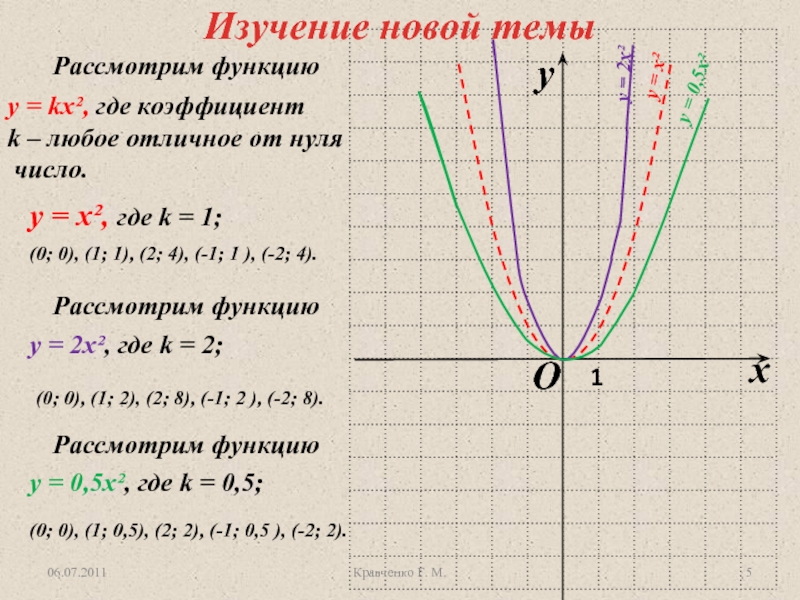
Слайд 5у = х², где k = 1;
у = х²
Изучение
новой темы
Рассмотрим функцию
у = 2х², где k =
2; Рассмотрим функцию
у = 0,5х², где k = 0,5;
(0; 0), (1; 2), (2; 8), (-1; 2 ), (-2; 8).
(0; 0), (1; 1), (2; 4), (-1; 1 ), (-2; 4).
(0; 0), (1; 0,5), (2; 2), (-1; 0,5 ), (-2; 2).
у = 2х²
у = 0,5х²
06.07.2011
Кравченко Г. М.
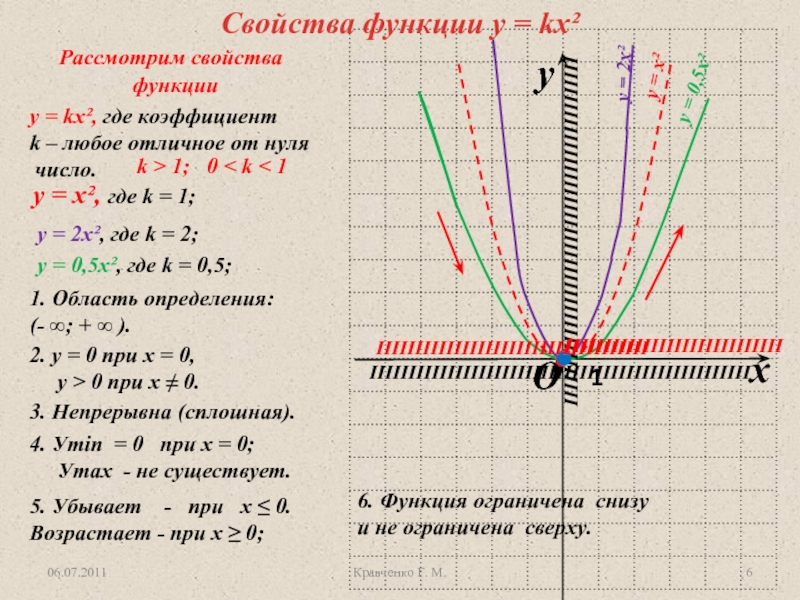
Слайд 6у = х², где k = 1;
у = х²
Свойства
функции y = kx²
у = 2х², где k
= 2; у = 0,5х², где k = 0,5;
у = 2х²
у = 0,5х²
k > 1; 0 < k < 1
5. Убывает - при х ≤ 0.
Возрастает - при х ≥ 0;
1. Область определения:
(- ∞; + ∞ ).
2. у = 0 при х = 0,
у > 0 при х ≠ 0.
3. Непрерывна (сплошная).
4. Уmin = 0 при х = 0;
Уmax - не существует.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
.
.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIIIIIIIIII
6. Функция ограничена снизу
и не ограничена сверху.
06.07.2011
Кравченко Г. М.
Слайд 7Свойства функции y = - kx²
у = - х², где
k = - 1;
у = - 2х²,
где k = - 2; у = - 0,5х², где k = - 0,5;
k < 0
Графики у = f(x) и у = - f(x)
симметричны относительно
оси ох.
1. Область определения:
(- ∞; + ∞ ).
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
2. у = 0 при х = 0,
у < 0 при х ≠ 0.
.
3. Непрерывна (сплошная).
4. Уmax = 0 при х = 0;
Уmin - не существует.
5. Возрастает - при х ≤ 0.
убывает - при х ≥ 0;
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
6. Функция ограничена сверху
и не ограничена снизу
06.07.2011
Кравченко Г. М.
Слайд 806.07.2011
Кравченко Г. М.
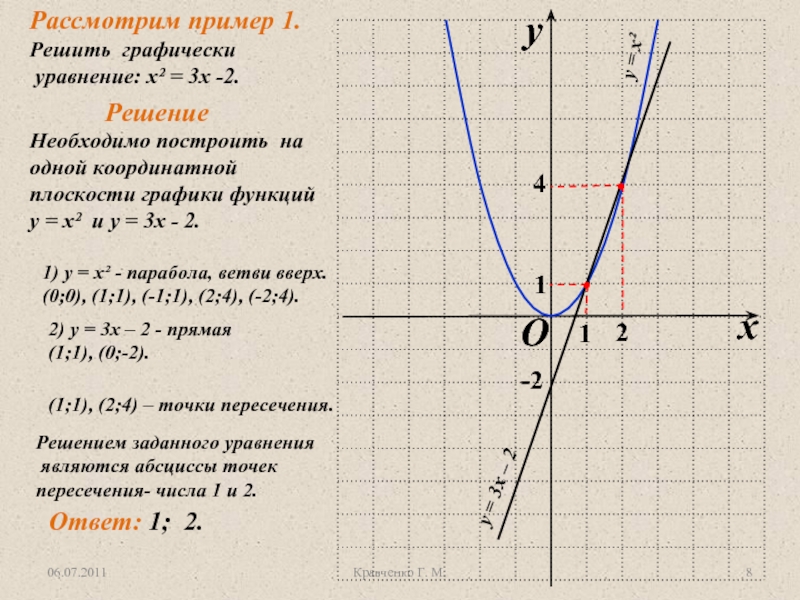
Рассмотрим пример 1.
Решить графически
уравнение: х² =
3х -2.
Решение
Необходимо построить на одной координатной плоскости графики функций
у = х² и у = 3х - 2.1) у = х² - парабола, ветви вверх.
(0;0), (1;1), (-1;1), (2;4), (-2;4).
2) у = 3х – 2 - прямая
(1;1), (0;-2).
1
-2
.
2
4
(1;1), (2;4) – точки пересечения.
Решением заданного уравнения
являются абсциссы точек
пересечения- числа 1 и 2.
Ответ: 1; 2.
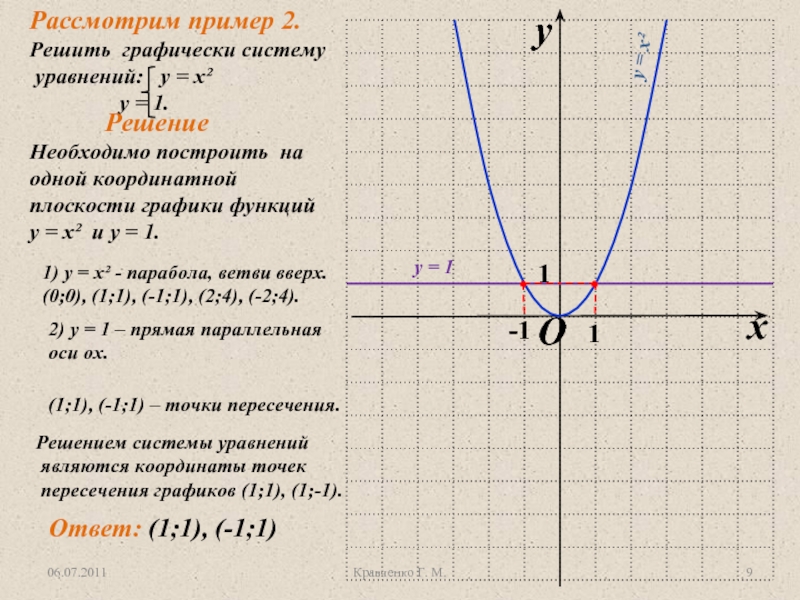
Слайд 9Необходимо построить на одной координатной плоскости графики функций у =
х² и у = 1.
Решение
1) у = х² -
парабола, ветви вверх.(0;0), (1;1), (-1;1), (2;4), (-2;4).
2) у = 1 – прямая параллельная
оси ох.
1
-1
(1;1), (-1;1) – точки пересечения.
Решением системы уравнений
являются координаты точек
пересечения графиков (1;1), (1;-1).
Ответ: (1;1), (-1;1)
06.07.2011
Кравченко Г. М.
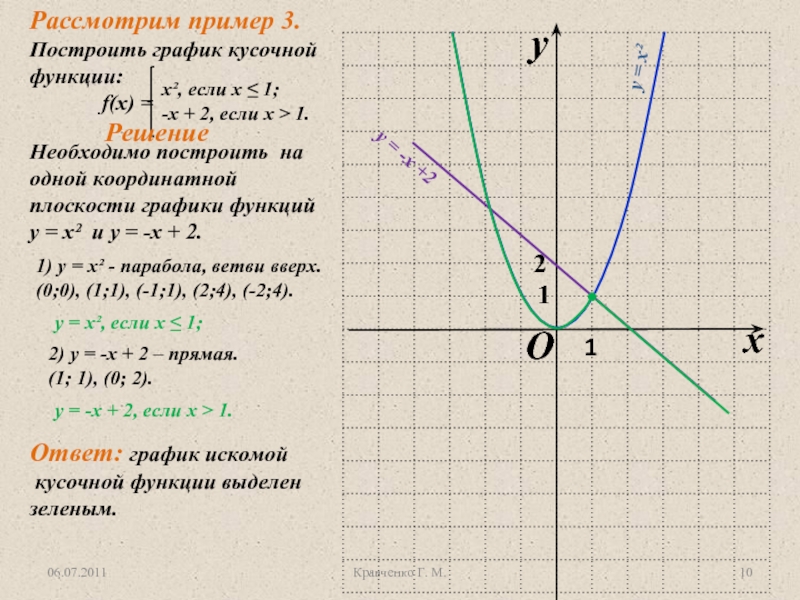
Слайд 1006.07.2011
Кравченко Г. М.
Решение
Необходимо построить на одной координатной плоскости графики
функций у = х² и у = -x + 2.
1)
у = х² - парабола, ветви вверх.(0;0), (1;1), (-1;1), (2;4), (-2;4).
y = x², если х ≤ 1;
2) у = -x + 2 – прямая.
(1; 1), (0; 2).
2
1
y = -х + 2, если х > 1.
Ответ: график искомой
кусочной функции выделен
зеленым.
Слайд 11Ответить на вопросы:
01.07.2011
Кравченко Г. М.
Назвать свойства функций у = kx
+ b, у = х².
Назвать свойства функции у =
kx², если k>1, 0Назвать порядок решения уравнений графическим способом.
Как графически решить систему уравнений?
Способ построения графиков функций, заданных несколькими условиями (кусочная функция).
Теги
