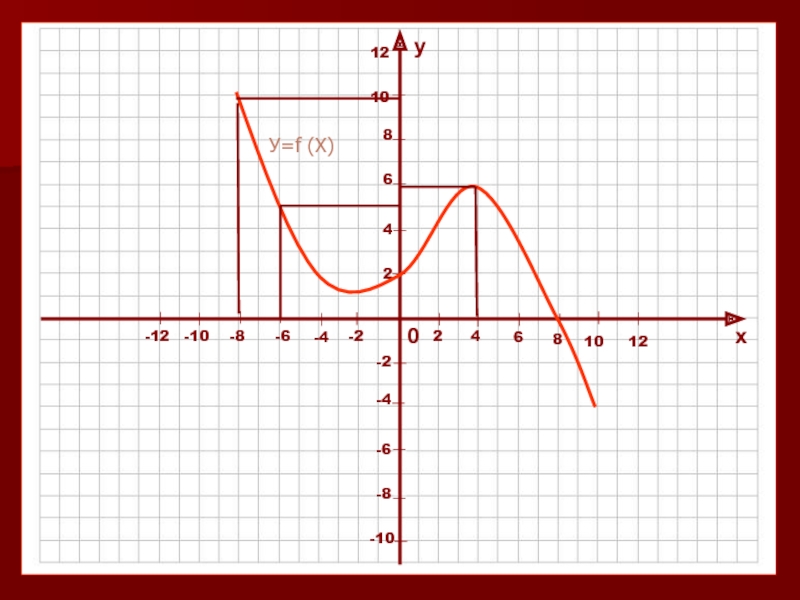
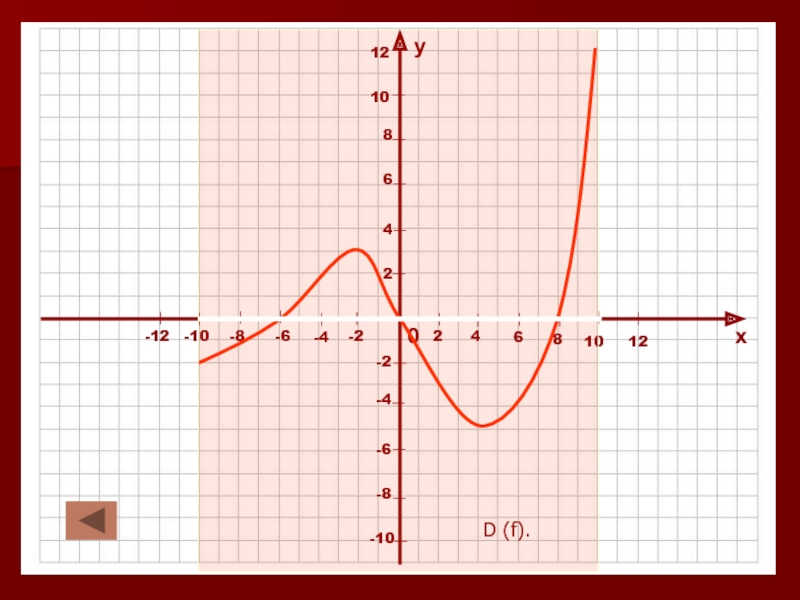
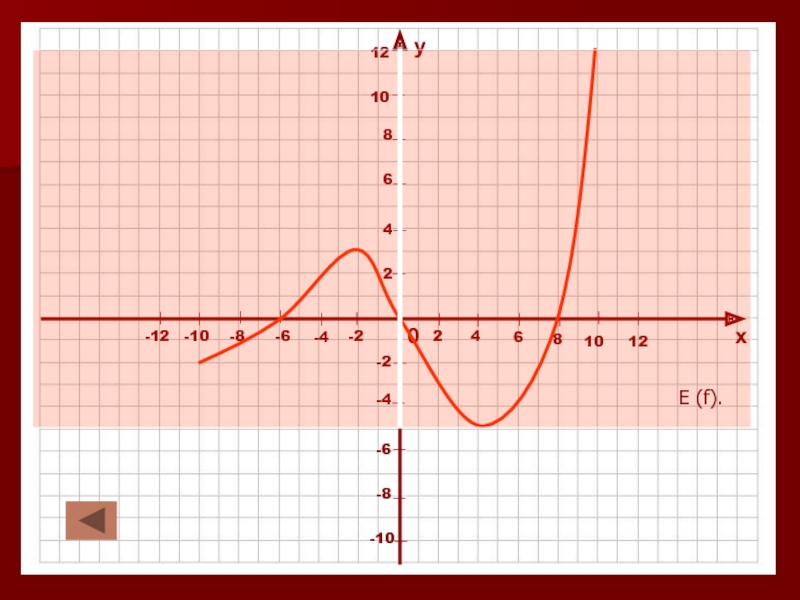
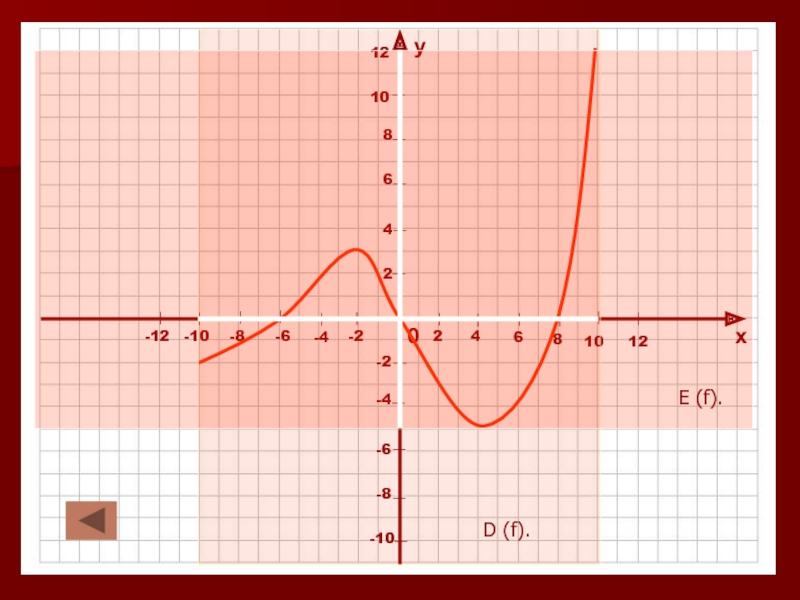
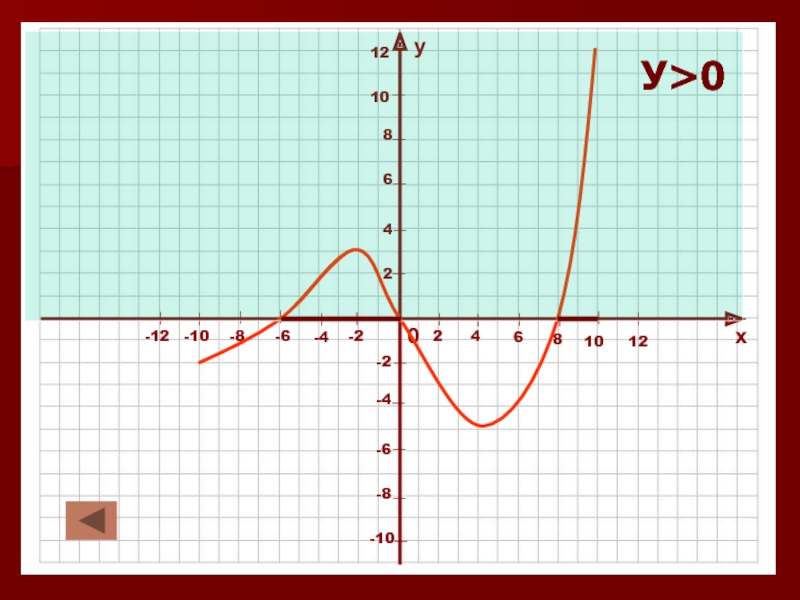
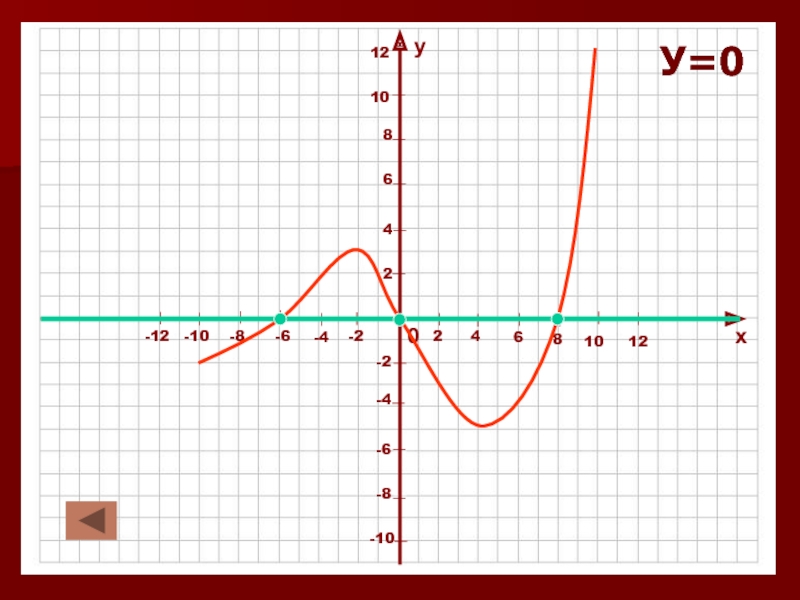
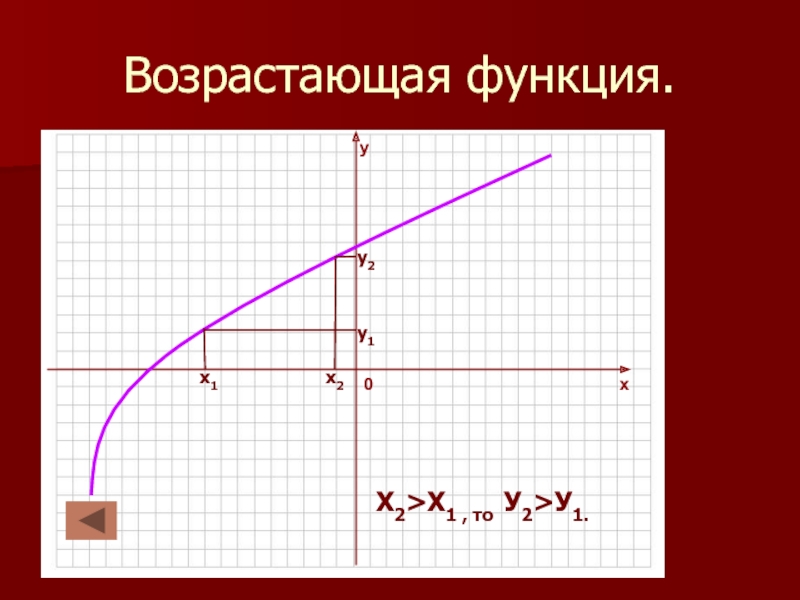
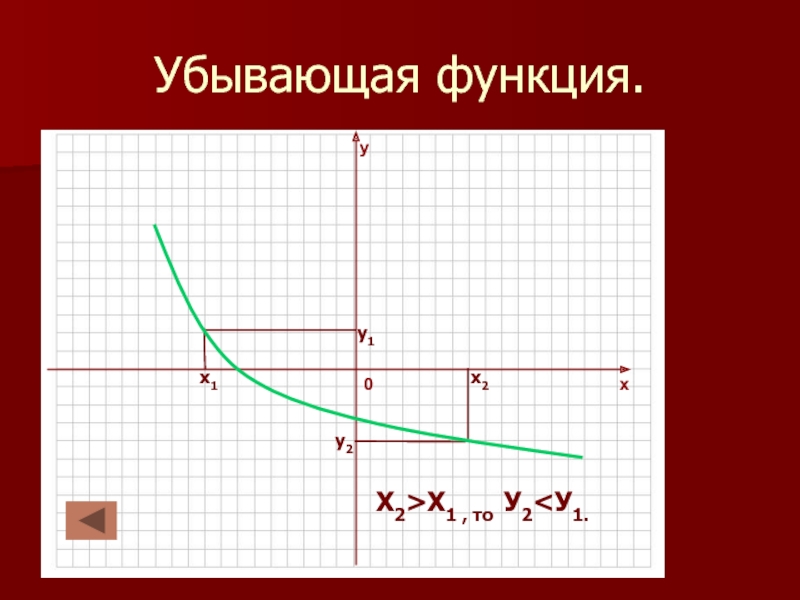
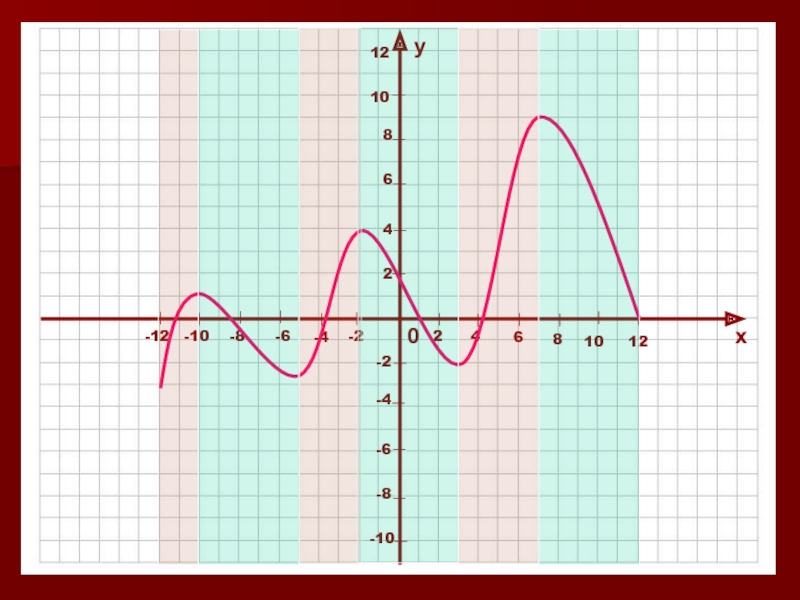
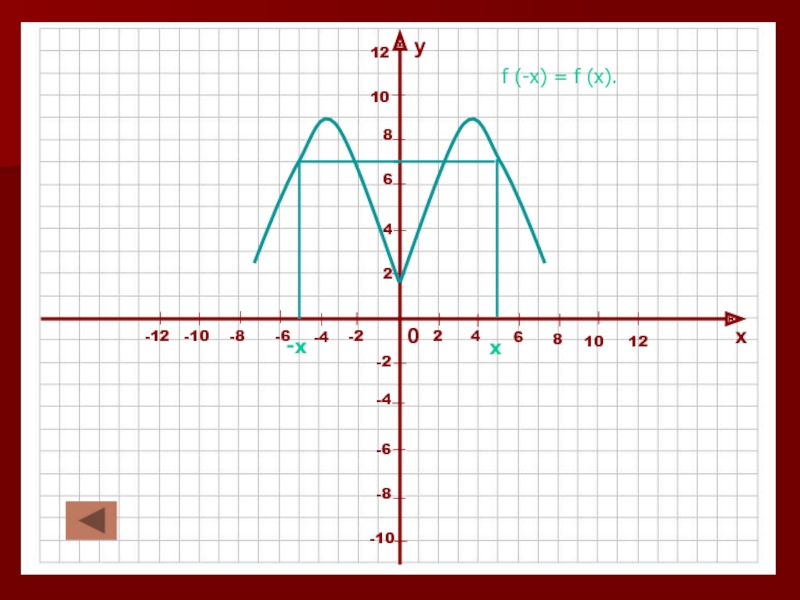
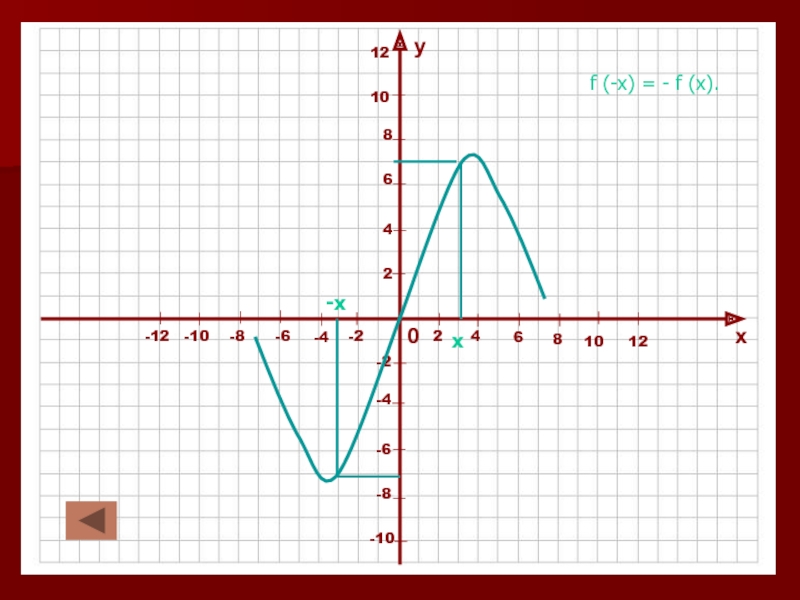
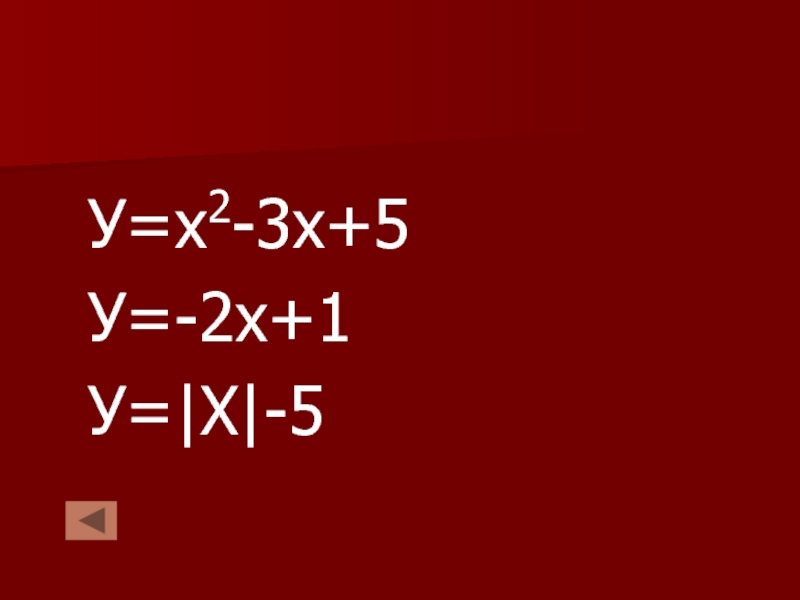Разделы презентаций

Функции и их свойства. Алгебра 9 класс

Содержание

Что такое «функция»?

Слайды и текст этой презентации

Слайд 1Функции и их свойства.
Алгебра 9 класс.

Функции и их свойства.Алгебра 9 класс.

Слайд 2Что такое «функция»?

Что такое «функция»?

Слайд 3
У=f (X)

У=f (X)

Слайд 4Определение функции.
Функцией называется зависимость между двумя переменными (У и Х)

в которой каждому значению независимой переменной (Х) соответствует единственное значение

зависимой переменной (У).

Независимую переменную называют - аргумент.

Значения зависимой переменной называют значениями функции.

Запись У=f (X) читается: У – функция от Х.
Определение функции.Функцией называется зависимость между двумя переменными (У и Х) в которой каждому значению независимой переменной (Х)

Слайд 5Способы задания функции.
Графически.

С помощью формулы.

Таблицей.

Словесный.

Рекуррентный.

Способы задания функции.Графически.С помощью формулы.Таблицей.Словесный.Рекуррентный.

Слайд 7У=х2-3х+5
У=-2х+1
У=|X|-5


У=х2-3х+5У=-2х+1У=|X|-5

Слайд 9Каждому натуральному числу поставим в соответствие его квадрат.

Каждому натуральному числу поставим в соответствие его квадрат.

Слайд 10а1=3, аn+1= 2аn-1.

а1=3, аn+1= 2аn-1.

Слайд 11Область определения и множество значений функции.
Все значения независимой переменной образуют

область определения функции -D (f).

Все значения, которые принимает зависимая переменная,

образуют область значений функции – E (f).
Область определения и множество значений функции.Все значения независимой переменной образуют область определения функции -D (f).Все значения, которые

Слайд 14



D (f).
E (f).

D (f).E (f).

Слайд 15 Если функция задана формулой и не указана ее

область определения, то считают, что область определения функции состоит из

всех значений аргумента, при которых формула имеет смысл.

Укажите область определения функций:


Если функция задана формулой и не указана ее область определения, то считают, что область определения

Слайд 16Промежутки знакопостоянства и нули функции.
1. Значения функции положительны. У>0

2. Значения

функции отрицательны. У

Промежутки знакопостоянства и нули функции.1. Значения функции положительны. У>02. Значения функции отрицательны. У

Слайд 20Монотонность функции.
Функция называется возрастающей на некотором промежутке, если большему значению

аргумента из этого промежутка соответствует большее значение функции.
Функция называется убывающей

на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Монотонность функции.Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение

Слайд 21Возрастающая функция.

х1
х2
у1
у2
Х2>Х1 , то У2>У1.

Возрастающая функция.х1х2у1у2Х2>Х1 , то У2>У1.

Слайд 22Убывающая функция.
х1
х2
у1
у2
Х2>Х1 , то У2

Убывающая функция.х1х2у1у2Х2>Х1 , то У2

Слайд 24Четные и нечетные функции.
Функция у = f (x) называется четной,

если для всех х из области определения функции выполняется равенство

f (-x) = f (x).

Функция у = f (x) называется нечетной, если для всех х из области определения функции выполняется равенство f (-x) = - f (x).


Четные и нечетные функции.Функция у = f (x) называется четной, если для всех х из области определения

Слайд 25-х
х
f (-x) = f (x).



-ххf (-x) = f (x).

Слайд 26-х
х
f (-x) = - f (x).



-ххf (-x) = - f (x).

Слайд 27Ограниченность функции.
Функция y=f (x) называется ограниченной снизу, если для любого

х из области определения функции выполняется условие

f (x)>a, где а – некоторое число.
Функция y=f (x) называется ограниченной сверху, если для любого х из области определения функции выполняется условие
f (x)< a, где а – некоторое число.
Функция называется ограниченной, если она ограничена и снизу, и сверху.




Ограниченность функции.Функция y=f (x) называется ограниченной снизу, если для любого х из области определения функции выполняется условие

Похожие презентации

Системы уравнений. Метод сложения 9 класс Системы уравнений. Метод сложения 9 класс 399
Элементы алгебры Элементы алгебры 520
Степенная функция Её свойства и график Степенная функция Её свойства и график 477
Свойства степени с натуральным показателем Свойства степени с натуральным показателем 391
Решение дробных рациональных уравнений Решение дробных рациональных уравнений 493
Метод интервалов решения неравенств Метод интервалов решения неравенств 354
Повторение курса алгебры 7 класса Повторение курса алгебры 7 класса 549
Преобразование графиков функций Преобразование графиков функций 447
Системы двух линейных уравнений с двумя переменными Системы двух линейных уравнений с двумя переменными 913
Метод введения новой переменной 9 класс Метод введения новой переменной 9 класс 460
Числовая окружность Числовая окружность 657
Описательная статистика Описательная статистика 405
Арифметическая прогрессия — презентация 9 класс Арифметическая прогрессия — презентация 9 класс 511
методы решения логарифмических уравнений методы решения логарифмических уравнений 537
Урок алгебры Урок алгебры "Теорема Виета" 8 класс 361
Введение в вычислительную математику Введение в вычислительную математику 619
Процентные вычисления в жизненных ситуациях Процентные вычисления в жизненных ситуациях 659
Решение заданий В9 Решение заданий В9 654
Презентация урока алгебры Презентация урока алгебры "Квадратные уравнения" 8 класс 365
Линейная функция и ее применение в физике Линейная функция и ее применение в физике 494

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика