Квадратичная функция и ее свойства

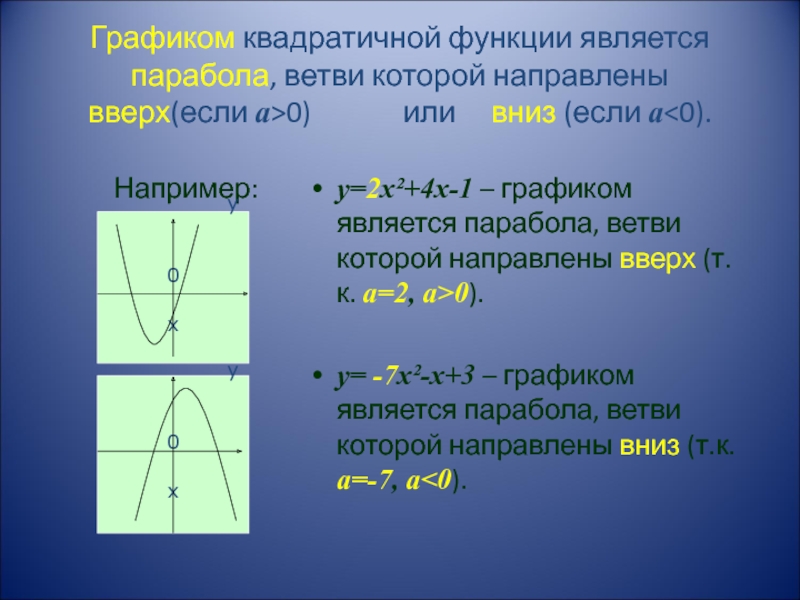
– заданные числа, а≠0,
х – действительная переменная, называется квадратичной функцией.
Примеры:
1)

или вниз

Например:

у=2х²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а>0).

у= -7х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а<0).

у


0
х

у


0
х

функции,
куда направлены ветви параболы.


Пример: у = х²-2х-3 –

координаты вершины параболы:

ах2+bх+с=0
С осью Оу: х=0

направление ветвей параболы.
2.
Найти координаты вершины параболы
(т; п).
3.
Провести ось симметрии.
4.
Определить

5.

Составить таблицу значений функции
с учетом оси симметрии параболы.

y = -х2-6х-8

Ось параболы х =-3
Таблица значений функции

промежутке
Функция убывает на промежутке
Наибольшее значение функции равно
(-4;-2)
(-∞;-4);(-2;∞)
(-∞;-3]
[-3;∞)
1, при х=-3

х=0 х=2

(0;1) (1;+∞)