Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция y=ax2. Её график и свойства. 9 класс
Содержание
- 1. Функция y=ax2. Её график и свойства. 9 класс
- 2. Сегодня на уроке:введем понятие квадратичной функциинаучимся строить график функции y=ax2изучим свойства функции y=ax2
- 3. Устная работа1 заданиеПрямая , параллельная ОхГиперболаПараболаПрямая, проходящая через (0;0)Прямая, параллельная оси Оу
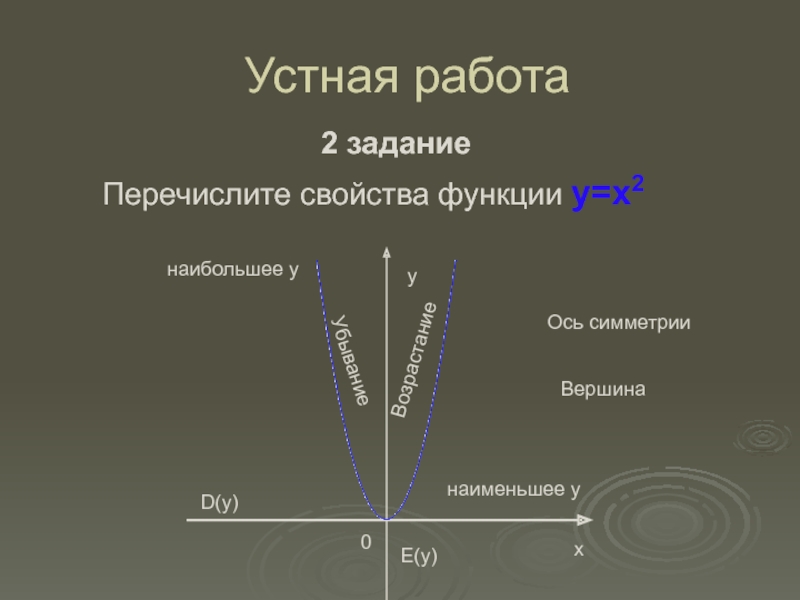
- 4. Устная работа2 заданиеПеречислите свойства функции y=x20ухD(y)E(y)ВозрастаниеУбываниенаименьшее унаибольшее уОсь симметрииВершина
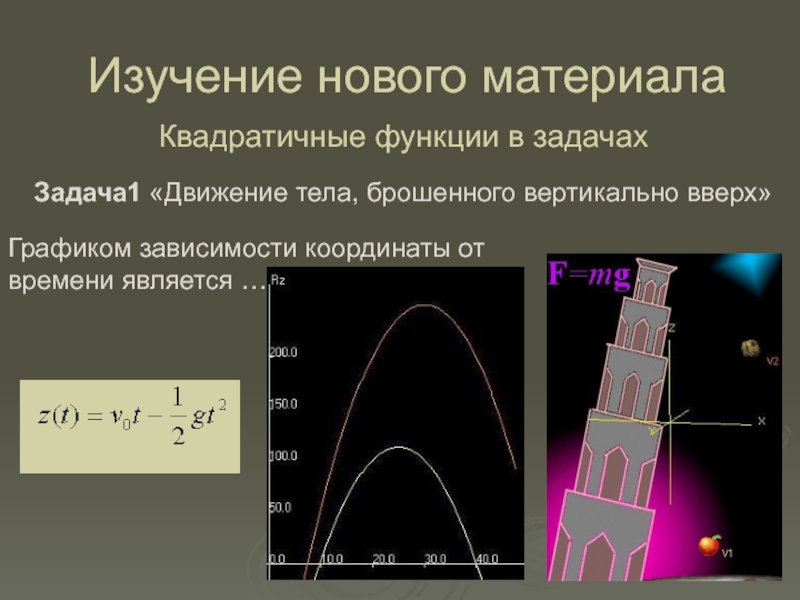
- 5. Изучение нового материалаКвадратичные функции в задачахЗадача1 «Движение
- 6. Выразим площадь дна коробки (х – глубина коробки)Квадратичные функции в задачахЗадача2 «Коробка из прямоугольного листа 30х40»S(x)=4x2-140x+1200
- 7. Примем боковую сторону куба за аКвадратичные функции в задачахЗадача3 «Площадь боковой поверхности куба»S(a)=4a2
- 8. Квадратичная функцияy=ax2+bx+ca, b, c – некоторые числаa = 0, x – независимая переменная
- 9. График и свойства функции у=ах2y(x)=2x2 y(x)=½x2 Начертите графики и запишите свойства функций
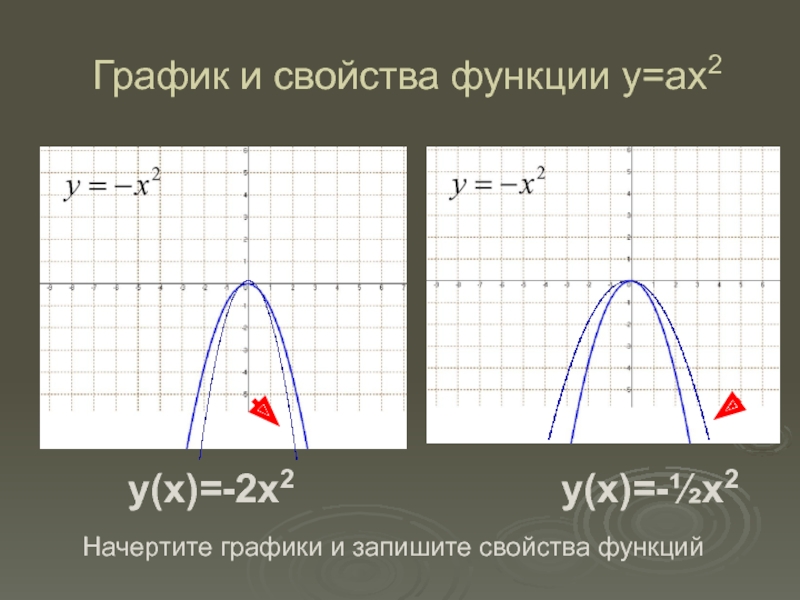
- 10. График и свойства функции у=ах2y(x)=-2x2 y(x)=-½x2 Начертите графики и запишите свойства функций
- 11. Тренировочные упражнения№ 90 – на доске и
- 12. Закрепим изученное: «Вопрос – ответ»
- 13. Что произойдёт с графиком функции у=х2, если функция изменится на у=-3х2?
- 14. Какую функцию называют квадратичной?
- 15. Назовите область значения функции у=-5х2
- 16. ОЦЕНКА «5»
- 17. Что произойдёт с графиком функции у=х2, если функция изменится на у=3,5х2?
- 18. Назовите промежутки возрастания и убывания функции у=ах2, если -1
- 19. Какое значение параметра а должно быть, чтобы функция у=ах2 не имела наибольшего значения?
- 20. Будет ли прямая у=9 пресекать график функции у=-3х2? Ответ обоснуйте.
- 21. Как называется точка пересечения параболы с её осью симметрии?
- 22. Домашнее заданиеп.5 (стр.28)№№ 91, 92, 96 (устно), 103заполнить таблицуСпасибо
- 23. Скачать презентанцию
Сегодня на уроке:введем понятие квадратичной функциинаучимся строить график функции y=ax2изучим свойства функции y=ax2
Слайды и текст этой презентации
Слайд 1Функция y=ax2.
Её график и свойства.
9 класс
Составила: Икрянова А.С.
Муниципальное общеобразовательное
учреждение - средняя общеобразовательная школа № 8 г.Армавир
Слайд 2Сегодня на уроке:
введем понятие квадратичной функции
научимся строить график функции y=ax2
изучим
свойства функции y=ax2
Слайд 3
Устная работа
1 задание
Прямая , параллельная Ох
Гипербола
Парабола
Прямая, проходящая через (0;0)
Прямая, параллельная
оси Оу
Слайд 4Устная работа
2 задание
Перечислите свойства функции y=x2
0
у
х
D(y)
E(y)
Возрастание
Убывание
наименьшее у
наибольшее у
Ось симметрии
Вершина
Слайд 5Изучение нового материала
Квадратичные функции в задачах
Задача1 «Движение тела, брошенного вертикально
вверх»
Графиком зависимости координаты от времени является …
.
Слайд 6Выразим площадь дна коробки (х – глубина коробки)
Квадратичные функции в
задачах
Задача2 «Коробка из прямоугольного листа 30х40»
S(x)=4x2-140x+1200
Слайд 7Примем боковую сторону куба за а
Квадратичные функции в задачах
Задача3 «Площадь
боковой поверхности куба»
S(a)=4a2
Слайд 9График и свойства функции у=ах2
y(x)=2x2
y(x)=½x2
Начертите графики и запишите
свойства функций
Слайд 10График и свойства функции у=ах2
y(x)=-2x2
y(x)=-½x2
Начертите графики и запишите
свойства функций
Слайд 11Тренировочные упражнения
№ 90 – на доске и в тетрадях
(на
миллиметровой бумаге)
№ 94 – самостоятельно с последующей проверкой
№ 97 –
устноУпражнение для повторения
№ 104 – по вариантам с последующей проверкой