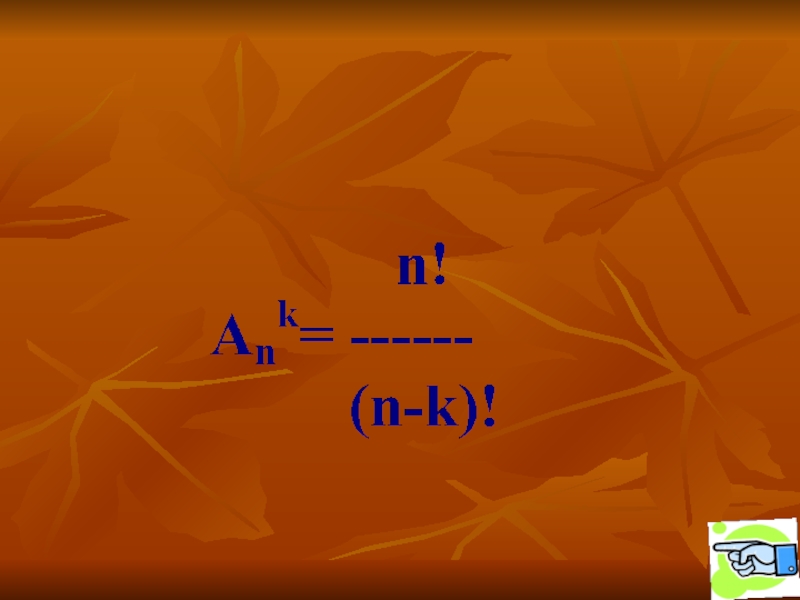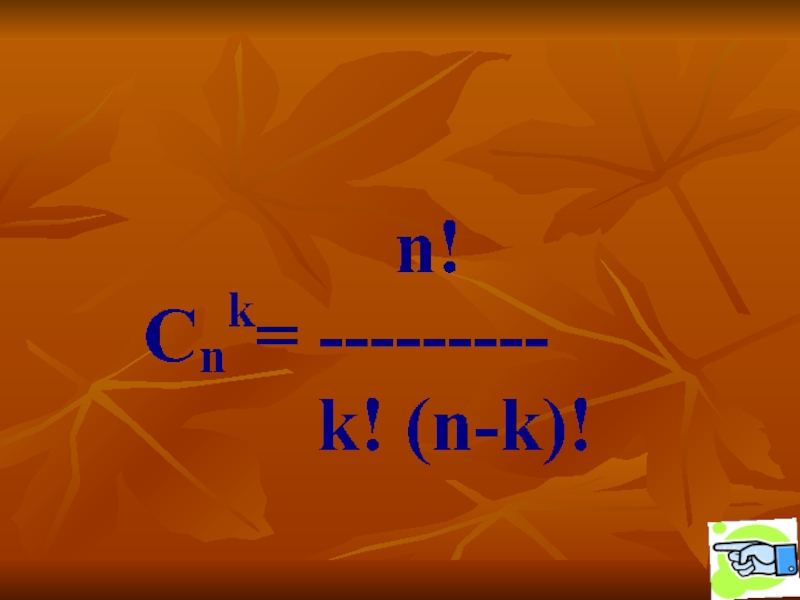Элементы комбинаторики

различные виды комбинаторных задач

перестановки?
Записать формулу для нахождения числа перестановок?
Что такое факториал?
Что такое размещения?
Записать

формулуформулу для нахождения числа размещений?
Что такое сочетания?
Записать формулу для нахождения числа сочетаний?
В чём различие между перестановками, размещениями и сочетаниями?

на перемене к теннисному столу, за которым уже шла игра.

Сколькими способами подбежавшие к столу восьмиклассники могут занять очередь для игры в настольный теннис? (решение)
№2 Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках? (решение)
№3 Учащиеся 2 класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета? (решение)
№4 Из набора, состоящего из 15 красок, надо выбрать 3 краски для окрашивания шкатулки. Сколькими способами можно сделать этот выбор? (решение)
Далее
Устал - отдохни

вторым – любой из оставшихся трёх, третьим – любой из

оставшихся двух и четвёртым - последний. По правилу произведения :4*3*2*1=24 способа.
№2 Число способов равно числу перестановок из 8 элементов : Р8=8!=1*2*3*4*5*6*7*8=40 320
№3 Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо набором предметов, либо порядком их следования. Имеем размещения из 9 по 4:


№4 Каждый набор трёх красок отличается от другого хотя бы одной краской. Имеем сочетания из 15 по 3 :.

тренер может выбрать из них для предстоящего турнира : а)

команду из четырёх человек; б) команду из четырёх человек, указав при этом, кто из членов команды будет играть на первой, второй, третьей и четвёртой досках?

№2 У Антона 6 друзей. Он может пригласить в гости одного или несколько из них. Определите общее число возможных вариантов.
№3 В 9 «а» классе учатся 25 учащихся, в 9 «б» - 20 учащихся, а в 9 «в» - 18 учащихся. Для работы на пришкольном участке надо выделить трёх учащихся из 9 «а», двух -из 9 «б» и одного – из 9 «в». Сколько существует способов выбора учащихся для работы на пришкольном участке?

С №1 Пять мальчиков и четыре девочки хотят сесть на девятиместную скамейку так, чтобы каждая девочка сидела между двумя мальчиками. Сколькими способами они могут это сделать?
№2 Из 12 солдат, в число которых входят Иванов и Петров, надо отправить в наряд трёх человек. Сколькими способами это можно сделать, если: а) Иванов и Петров должны пойти в наряд обязательно; б) Иванов и Петров должны остаться; в)Иванов
должен пойти в наряд, а Петров –остаться?
(Ответы)
Устал - отдохни

43 680 способов.
№2 63 способа,
указание:С61+С62+С63+С64+С65+С66.
№3 7 866

000 способов,
указание:С253*С202*С181 .
С №1 2880 способов,
указание:Р5*Р4 .
№2 а)10 способов;
б)120 способов;
в)45 способов.

сколько различных комбинаций (всевозможных объединений элементов), подчиненных тем или иным

условиям, можно составить из элементов, принадлежащих данному множеству.
Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать».

один за другим некоторые k элементов. Если первый элемент можно

выбрать способами, после чего второй элемент можно выбрать из оставшихся элементов способами, затем третий элемент – способами и т.д., то число способов, которыми могут быть выбраны все k элементов, равно произведению:

в них элементов, называются перестановками из n элементов.
Перестановки из

n элементов обозначают Pn и вычисляют по формуле: Pn=n!
n!=1*2*3*4*…*n (n факториал)
Свойство: 0!=1
Задача: Сколькими способами могут разместиться 5 пассажиров в пятиместной каюте?
Решение: P5=5!=1*2*3*4*5=120

множество, состоящее из k элементов, взятых в определённом порядке из

данных n элементов.
Число размещений из n элементов по k обозначаются (читается: «А из n по k»)

из k элементов, выбранных из данных n элементов (не имеет

значения, в каком порядке указаны элементы).
Число сочетаний из n элементов по k обозначают (читается: «С из n по k»).

МОЛОДЦЫ!

СПАСИБО ЗА УРОК!