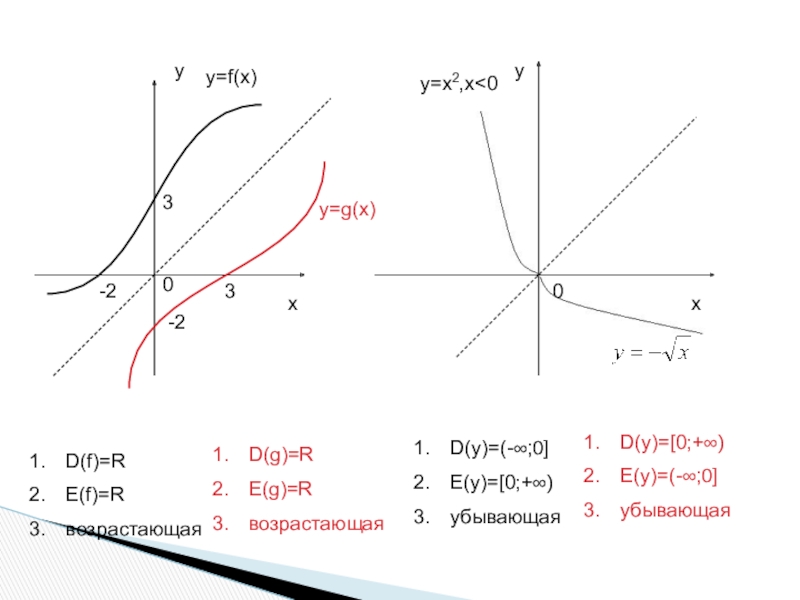
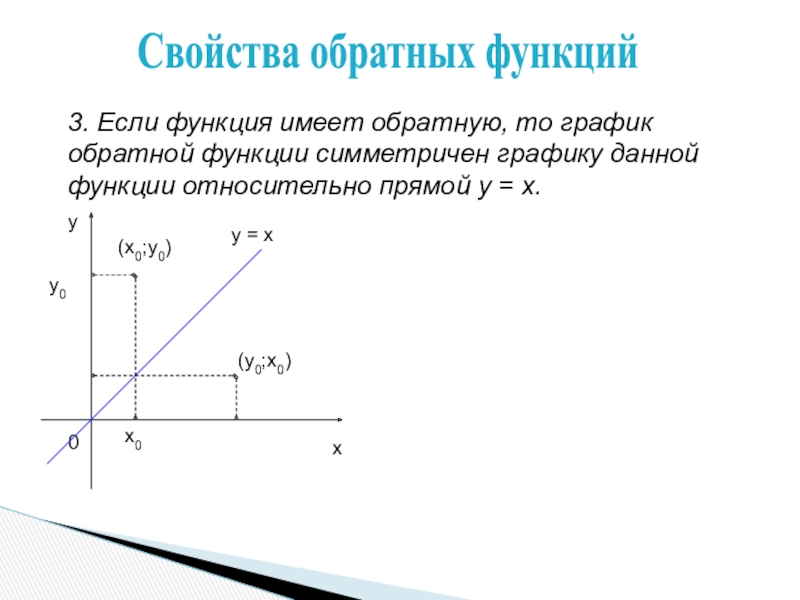
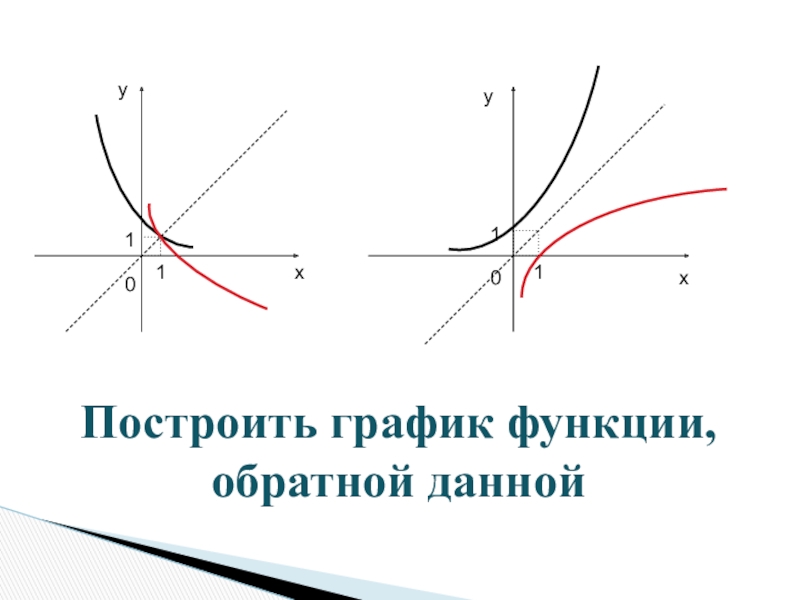
изучать свойства обратимости функции и нахождение функции обратной данной.
Развивающая:
овладеть понятием
обратной функции и усвоить методы нахождения обратной функции;развивать навыки самоконтроля, предметную речь.
Воспитательная:
формировать коммуникативную компетентность.
Цель урока: