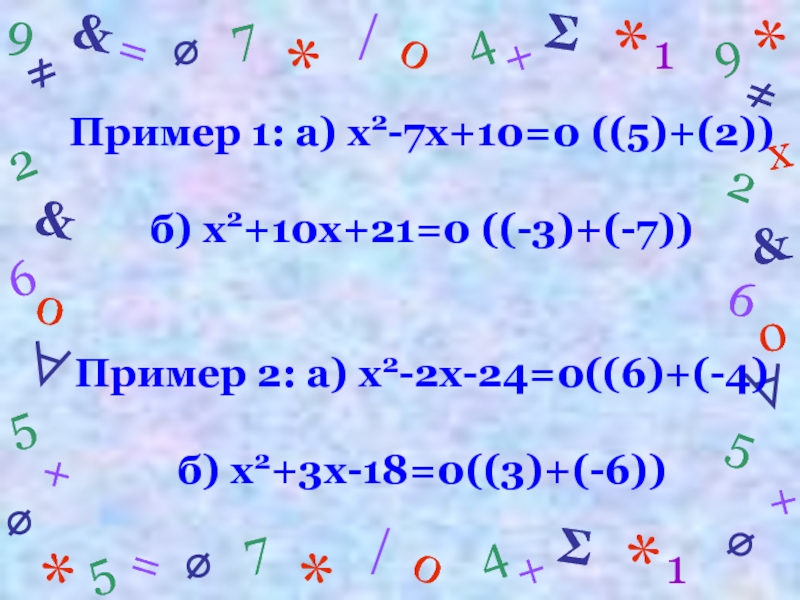Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нестандартные приемы решения квадратных уравнений
Содержание
- 1. Нестандартные приемы решения квадратных уравнений
- 2. Нестандартные приёмы решения квадратных уравнений х2+4х-5=0 у2+bу+са=05х2+7х+2=0(b+d)x-x2=bd
- 3. Актуальность темы исходит из особенности нашего времени
- 4. Тема «Квадратные уравнения» занимает в математике одно
- 5. Поэтому, проблема решения квадратных уравнений нестандартными методами,
- 6. Объект исследования - процесс обучения учащихся 8
- 7. Гипотеза – обучение, подготовка и сдача конкурсных
- 8. Практическая значимость: материал данной работы может использоваться
- 9. Слайд 9
- 10. Слайд 10
- 11. «Предмет математики настолько
- 12. Приведённые квадратные уравнения можно решать устно по
- 13. ∅Σ∀≠&56147092+=*/∅∀≠&56х092+0*∅5+*Σ147=/0*∅+*&* Пример
- 14. Не каждое приведённое уравнение можно решать устноНапример,
- 15. Слайд 15
- 16. Метод введения новой переменной Пример: (5х
- 17. Слайд 17
- 18. Метод «переброски» старшего коэффициентаах2 + bx +
- 19. Пример: 2х2 - 11 + 15 =0
- 20. Пример:Х2 + 1,5х - 2,5 =
- 21. Решение квадратных уравнений с применением циркуля и линейки
- 22. Пример1: Х2 – 2х + 1 =
- 23. История развития квадратных уравнений: Квадратные
- 24. Слайд 24
- 25. Квадратные уравнения в Древнем Вавилоне:
- 26. Квадратные уравнения в Европе в 13
- 27. Квадратные уравнения в Индии: Задачи
- 28. Квадратные уравнения в Древней Греции:Квадратные уравнения также
- 29. Знаменитый физик Альберт
- 30. Спасибо за внимание
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1МКОУ – Савкинская СОШ Презентация по теме: «Нестандартные приемы решения квадратных
уравнений»
Учителя математики первой квалификационной категории
Штабрат Ольги Анатольевны
Слайд 3Актуальность темы исходит из особенности нашего времени – это потребность
в предприимчивых, деловых, компетентных специалистах в той или иной сфере
деятельности. Необходимо быть грамотным, чтобы нормально «функционировать в сложном и требовательном обществе». А быть грамотным в быстро меняющемся мире означает быть просто лучше образованным. Чем выше уровень образованности, тем выше профессиональная и социальная мобильность. Кроме того, анализ единого государственного экзамена показывает, что не менее 50% предлагаемых задач с параметрами так или иначе связано с нахождением корней квадратного трехчлена.Слайд 4Тема «Квадратные уравнения» занимает в математике одно из центральных мест.
Разнообразие задач относящихся к теме работы, очень велико. Они часто
входят в состав решения более сложных задач математики и физики. Недаром среди математиков популярна такая фраза «Во многих задачах торчат уши квадратного уравнения». Вот эти «уши» и надо заметить, чтобы сообразить, как получить ответ.Слайд 5Поэтому, проблема решения квадратных уравнений нестандартными методами, которые недостаточно освещены
в общем курсе школьной математики и совершенно необходимы каждому ученику,
желающему хорошо подготовиться для успешной сдачи конкурсных экзаменов, а также для успешных выступлений на математических олимпиадах, будет существовать.Слайд 6Объект исследования - процесс обучения учащихся 8 класса . Предмет исследования
– формирование умений и навыков учащихся 8 класса по решению
квадратных уравнений нестандартными методами в процессе обучения их по данной теме.Слайд 7Гипотеза – обучение, подготовка и сдача конкурсных экзаменов, выступление на
математических олимпиадах будет проходить успешнее, если в процессе обучения научить
школьников нестандартным приемам решения квадратных уравнений.Слайд 8Практическая значимость: материал данной работы может использоваться как на уроках
математики в 8-9 классах, так и на занятиях кружков. Он
способствует развитию познавательных интересов, мышления учащихся, предоставляет возможность подготовиться к сознательному выбору профиля обучения и дальнейшей специализации.Слайд 9
расширить
и углубить представления о решение
квадратных уравнений через применение нестандартных методов ЦЕЛЬ РАБОТЫ -
Слайд 10
Задачи:
Проанализировать
методическую и специальную литературу по данной теме.
Научить учащихся решать квадратные
уравнения более высокой, по сравнению с обязательным уровнем, сложности. Слайд 11 «Предмет математики настолько серьёзен, что
нужно не упускать случая делать его немного занимательным».
Блез Паскаль «Уравнение – это золотой ключ, открывающий все математические сезамы».
С. Коваль
Слайд 12Приведённые квадратные уравнения можно решать устно по обратной теореме Виета:
Произведение корней приведённого квадратного уравнения равно свободному члену с тем
же знаком, а сумма корней-второму коэффициенту с противоноложным знаком.Слайд 13∅
Σ
∀
≠
&
5
6
1
4
7
0
9
2
+
=
*
/
∅
∀
≠
&
5
6
х
0
9
2
+
0
*
∅
5
+
*
Σ
1
4
7
=
/
0
*
∅
+
*
&
*
Пример 1: а) х2-7х+10=0 ((5)+(2))
б) х2+10х+21=0 ((-3)+(-7)) Пример 2: а) х2-2х-24=0((6)+(-4) б) х2+3х-18=0((3)+(-6))
Слайд 14Не каждое приведённое уравнение можно решать устно
Например, х2 + 3х
+1 =0
х1,2 = или х2 – 2х + 5 = 0
D = 4 – 20 = -16
Слайд 15
Метод разложения на множители
Пример: 3х2 + 2х – 1 = 0
3х2 + 3х – х – 1 = 0
3х(х + 1) – (х + 1) = 0
(х + 1) (3х – 1) = 0
х + 1 = 0 или 3х – 1 = 0
х = -1 или х =
ответ: -1;
Слайд 16Метод введения новой переменной
Пример: (5х + 3)2 =
3(5х + 3) – 2
Пусть 5х + 3 = t, тогда t2 = 3t – 2
t2 - 3t + 2 = 0
D > 0, то t1 = 1 t 2 = 2
Если t = 1, то 5х + 3 = 1; х = -0,4
Если t = 2, то 5х + 3 = 2; х = -0,2
Ответ: -0,4; -0,2
Слайд 17
Использование свойства коэффициентов квадратного уравнения
х2 + 4х – 5 = 0 х2 + 6х + 5 = 0
а = 1, b =4, c =-5 a = 1, b = 6, c = 5
a + b + c = 0 a + c = b
x1 = 1, x2 = -5 x1 = -1, x2 = -5
ax2 + bx + c = 0 (a ≠ 0)
Если а + b + c = 0, то х1 = 1; х2 =
Если а + с = b, то х1 = -1; х2 = -
Например, 5х2 + 7х + 2 = 0 х1 = -1; х2 = -
или 5х2 + 7х =0 х1 = -1; х2 =
Слайд 18Метод «переброски» старшего коэффициента
ах2 + bx + c = 0;
a2x2 + bax + ca = 0
Пусть ах = у,
тогда у2 + bу + са = 0
Так как ах1 = у1 , ах2 = у2 , то
х1 = , х2 =
Слайд 19Пример: 2х2 - 11 + 15 =0 22 · х2 -
2 · 11х + 30 =0 Пусть 2х = у ,
тогда у2 - 11у + 30=0 у1 = 5 , у2 = 6 Тогда 2х1 = 5 , 2х2 = 6; х1 = 2,5 , х2 = 3 Ответ: 2, 5 ; 3Слайд 20
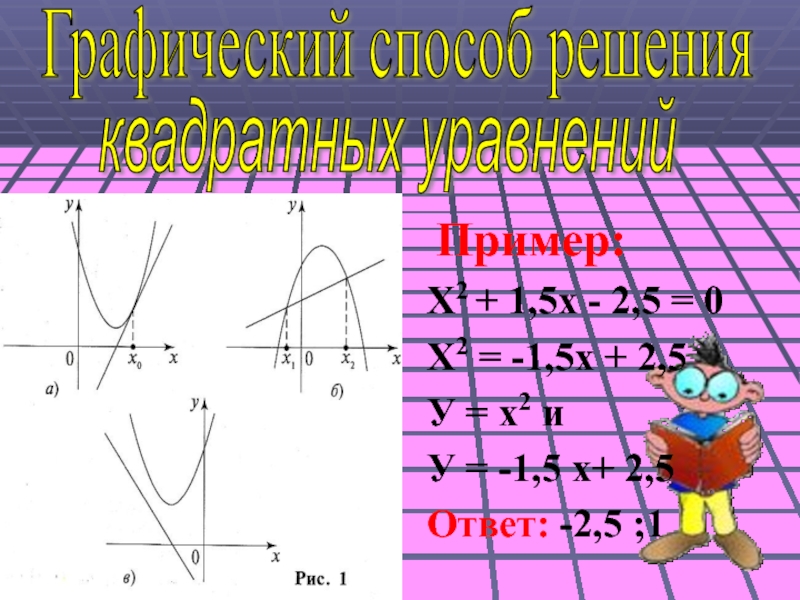
Пример:
Х2 + 1,5х - 2,5 = 0
Х2 = -1,5х
+ 2,5
У = х2 и
У = -1,5 х+ 2,5
Ответ:
-2,5 ;1 Графический способ решения
квадратных уравнений
Слайд 22Пример1: Х2 – 2х + 1 = 0
Ответ: 1 Пример2: Х2 + 4х – 5 = 0 Ответ: -5 ; 1 Пример3: Х2 – 4х + 5 = 0 Ответ: нет корней
Слайд 23
История развития квадратных уравнений:
Квадратные уравнения в
Багдаде(9 век)
Квадратные уравнения в Древнем Вавилоне.
Квадратные
уравнения в Индии.Квадратные уравнения в Европе 13-17 в.в.
Квадратные уравнения в Древней Греции.
X2+bx+c=0
Слайд 24
Квадратные уравнения в Багдаде(9 век):
Впервые квадратные уравнения появились в городе Багдаде, их вывел приглашённый математик из города Хорезм(Ныне территория Узбекистана) Мухаммед бен-Муса Ал-Хорезми. В отличие от греков, решавших квадратные уравнения геометрическим путём, он мог решить любые квадратные уравнения по общему правилу (найти положительные корни). Если у греков было геометрическое решение, то метод ал-Хорезми почти алгебраический.
Слайд 25
Квадратные уравнения в Древнем Вавилоне:
Необходимость решать уравнения
не только первой, но и второй степени ещё в древности
была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а так же с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне.Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратных уравнений.
Слайд 26
Квадратные уравнения в Европе в 13 - 17 веках:
Формулы решения квадратных уравнений в Европе были впервые изложены
в 1202 году итальянским математиком Леонардо Фибоначчи.Общее правило решения квадратных уравнений, приведённых к единому каноническому виду ax2+bx+c=0, было сформулировано в Европе лишь в 1544 году Штифелем .
Слайд 27Квадратные уравнения в Индии:
Задачи на квадратные уравнения
встречались уже в 499 году.
В Древней Индии
были распространены публичные соревнования в решении трудных задач.В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звёзды, так учёный человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи.»
Слайд 28Квадратные уравнения в Древней Греции:
Квадратные уравнения также решали и в
Древней Греции. Среди математиков Древней Греции было принято выражать
алгебраические утверждения в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, произведение истолковали как площадь прямоугольника, а произведение трёх чисел-как объём прямоугольного параллепипеда. Например, говорили, что площадь квадрата, построенного на сумме двух отрезков, равна сумме площадей квадратов, построенных на этих отрезках, увеличенной на удвоенную площадь прямоугольника. С того времени идут термины «квадрат числа», «куб числа». Квадратные уравнения греки также решали геометрически. Примеры решения уравнений без обращения к геометрии даёт Диофант. Особое внимание уделял неопределённым уравнениям, теория которых называетсятеперь «диофантовым анализом».