Площадь криволинейной трапеции ИНТЕГРАЛ

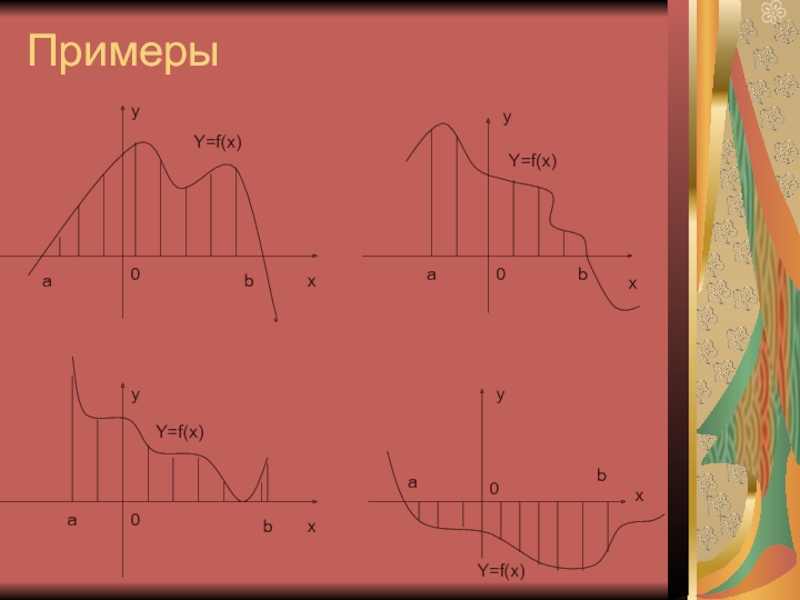
фигуры ограниченной линиями
Формулы для нахождения площади различных фигур
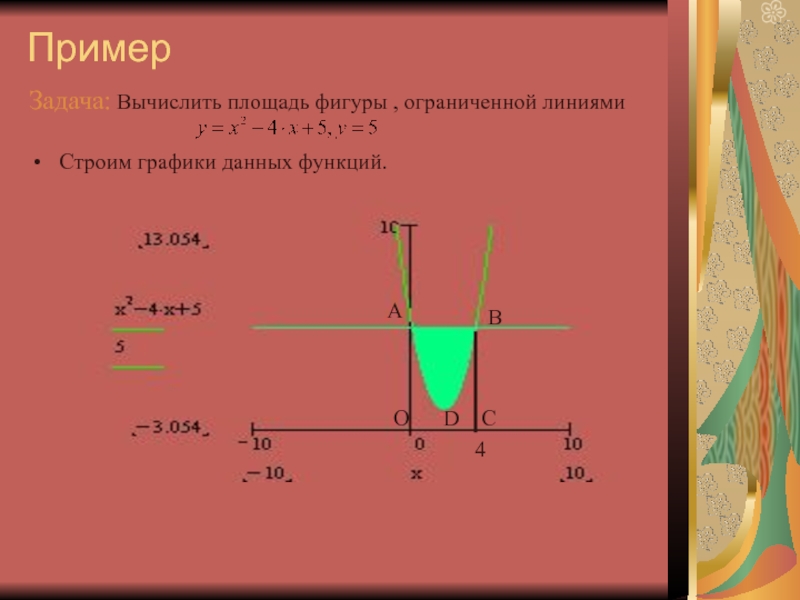
Пример вычисления площади

фигуры, ограниченной линиями
Дифференцированные задания для самоконтроля

f(x), не имеющая на нем знака. Фигуру, ограниченную графиком этой

функции, отрезком [а;b] и прямыми x = а и x=b, называют криволинейной трапецией.

x=а

x=b

Y=f(x)

x

y

и y=g(x).
1. Строим (точно) график данных функций.
2.Найдём абсциссы

точек их пересечения (границы интегрирования) из уравнения: f(x)=g(x).
Решаем его, находим x1=a,x2=b.
3.Выделяем свою фигуру. Выясняем, является ли данная фигура криволинейной трапецией.
4.Ищем площадь данной фигуры:
Площадь криволинейной трапеции находим по формуле Ньютона-Лейбница:


где F(x) – первообразная для f(x).

x

y

a

b

A

C

B

n

Y=f(x)

Y=g(x)

ниже оси Ох (f(x)

формуле :

2. Если фигура ограничена кривыми y=f(x) и y=g(x), прямыми x=a, x=b (при условии ),
то её площадь можно вычислить по формуле:


3.

x

y

a

b

F(x)

x

y

g(x)

f(x)

a

b

0

0

S1

S2

S3

a

b

y

x

следовательно, искомую площадь можно получить как разность площадей прямоугольника АBCO

и криволинейной трапеции АОCBD.

Варианты ответа: а) 2; б) 4; в) 3,1; г) 6,5.

2. y=5,
Варианты ответа: а) ; б) 6; в) 8,4; г) 6.
3. y=0, y=3,
Варианты ответа: а)2 ; б) 0,5; в) 3; г) 6,1.

Варианты ответа: а)2/3 ,б)8/3 ,в)4/3 ,г)4/3.
2.y=0, x=

π/2 ,
Варианты ответа: а) 2 ,б) 1 ,в) 1/2 ,г)3/2.
3.y=0, x=2,
Варианты ответа: а) 4 ,б) 8 ,в) 8/3 ,г)2.

y=cos x
Варианты ответа: а)

,б) 3/7, в)0,2, г)6.
2. ,
Варианты ответа: а)-5/2, б) 3/8, в) 0,4, г) 3.
в точке с абсциссой x0=1.
Варианты ответа: а)2 ,б) 8, в)0,6, г)37.

4. Осью Ох и
Варианты ответа: а)2 ,б) 6, в)0,5, г)50.