Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной к исследованию функций
Содержание
- 1. Применение производной к исследованию функций
- 2. Понятие «производная» возникло в XVII веке в
- 3. Используя методы дифференциального исчисления английский астроном, математик
- 4. Найти производную функцииРазминка
- 5. Признак возрастания и убывания функции=
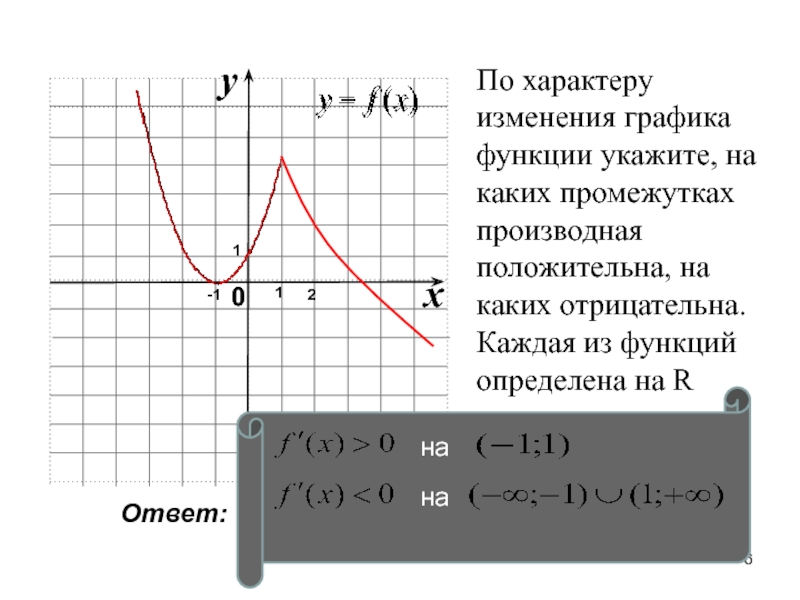
- 6. По характеру изменения графика функции укажите, на
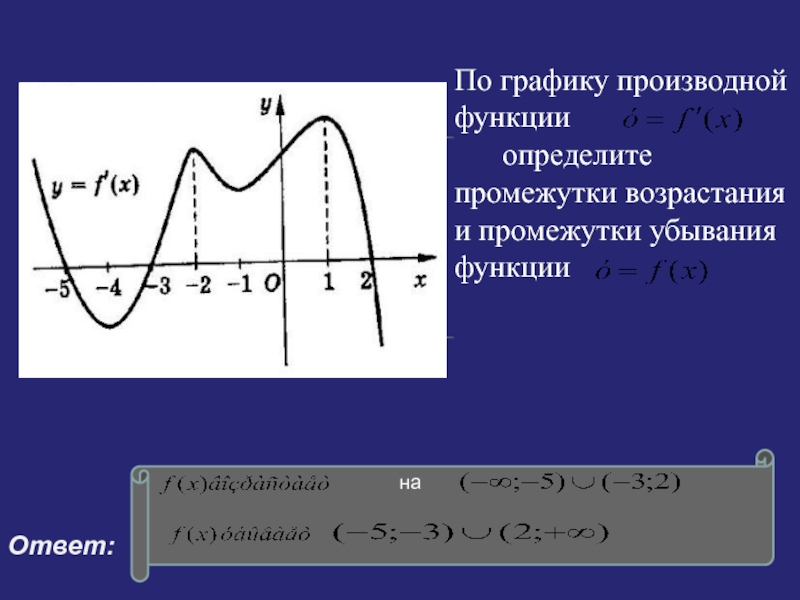
- 7. По графику производной функции определите промежутки возрастания и промежутки убывания функции Ответ:1
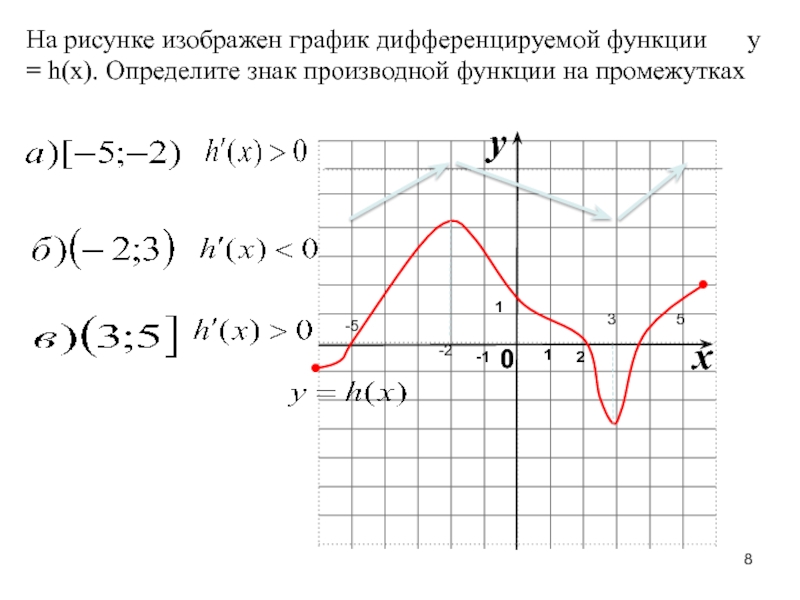
- 8. На рисунке изображен график дифференцируемой функции
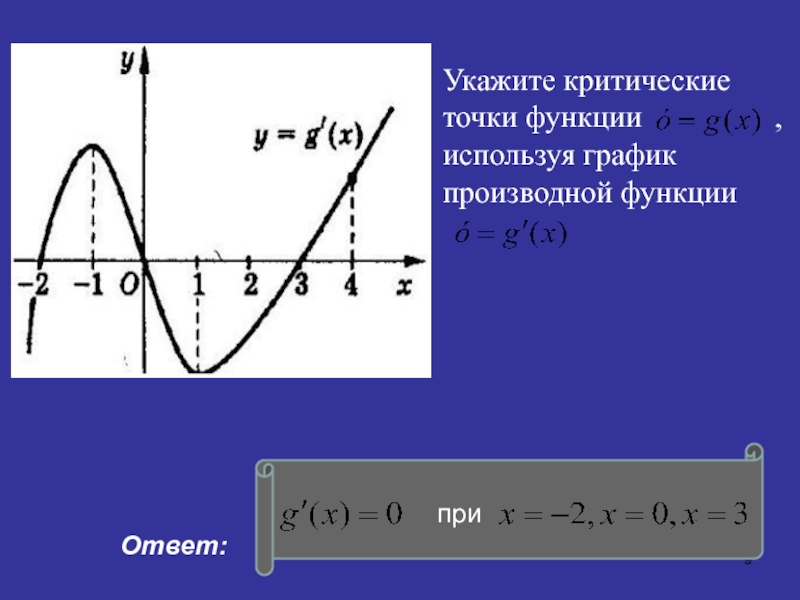
- 9. Укажите критические точки функции
- 10. 11-10ху-1ух10-11-1y=f(x)y=g(x) Касательная в таких точках графика
- 11. производная равна нулю(стационарные точки)критические точкипроизводная не существуетмаксимума«+»
- 12. Достаточное условие существования экстремума функции: Если при
- 13. Исследование функций с помощью производной и построение графиков функций.
- 14. Схема исследования функцииНайти область определения функции;Исследовать функцию
- 15. x12345-1-2-4-1-21-3-50возрастаетвозрастаетубываетПостроить эскиз графика функции, зная, чтоy-4
- 16. Образец выполнения работы.Оформление работы учеником.а)
- 17. Задачи на нахождение наибольшего и наименьшего значений
- 18. Правило нахождения наибольшего и наименьшего
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1презентация учителя математики
Верхнегерасимовской СШ І-ІІІ ступеней
Горбань Натальи Геннадиевны
Применение производной к исследованию функций
Слайд 2Понятие «производная» возникло в XVII веке в связи с необходимостью
решения ряда задач из физики, механики и математики.
Готфрид Вильгельм
фон ЛейбницИcаак Ньютон
25 декабря 1642 — 20 марта 1727
1 июля 1646 — 14 ноября 1716,
Слайд 3 Используя методы дифференциального исчисления английский астроном, математик Эдмон Галлей ещё
в XVII веке предсказал возвращение кометы Галлея.
(что, увы, было уже
после его смерти). Комета действительно возвратилась, как было предсказано, и позже была названа в его честь. Комета Галлея вернется во внутреннюю Солнечную систему в следующий раз в 2061 году.
В 1705 году Эдмонд Галлей предсказал, что комета, которую наблюдали в 1531, 1607 и 1682 годах, должна возвратиться в 1758 году
Слайд 6По характеру изменения графика функции укажите, на каких промежутках производная
положительна, на каких отрицательна. Каждая из функций определена на R
Ответ:
Слайд 7По графику производной функции
определите промежутки возрастания и промежутки
убывания функции
Ответ:
1
Слайд 8На рисунке изображен график дифференцируемой функции y =
h(x). Определите знак производной функции на промежутках
-2
3
-5
5
1
Слайд 101
1
-1
0
х
у
-1
у
х
1
0
-1
1
-1
y=f(x)
y=g(x)
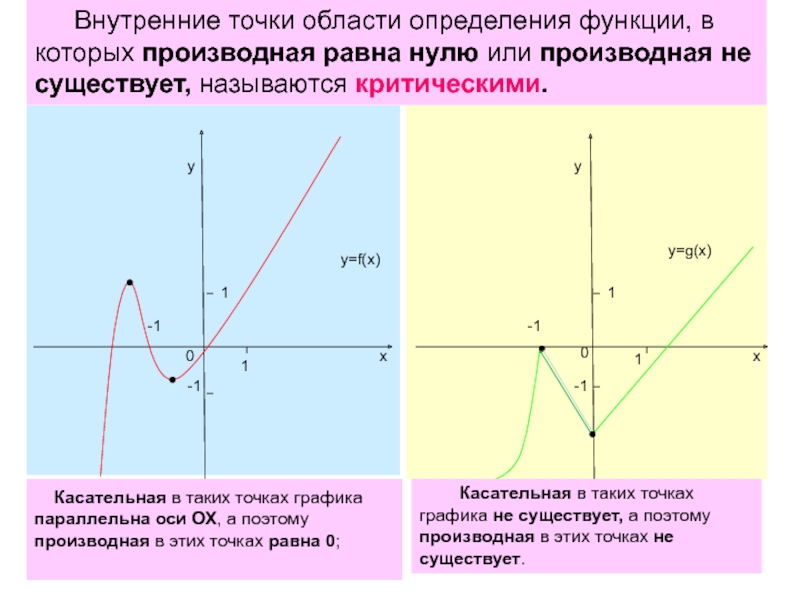
Касательная в таких точках графика параллельна оси ОХ,
а поэтому производная в этих точках равна 0;
Внутренние точки области
определения функции, в которых производная равна нулю или производная не существует, называются критическими. Касательная в таких точках графика не существует, а поэтому производная в этих точках не существует.
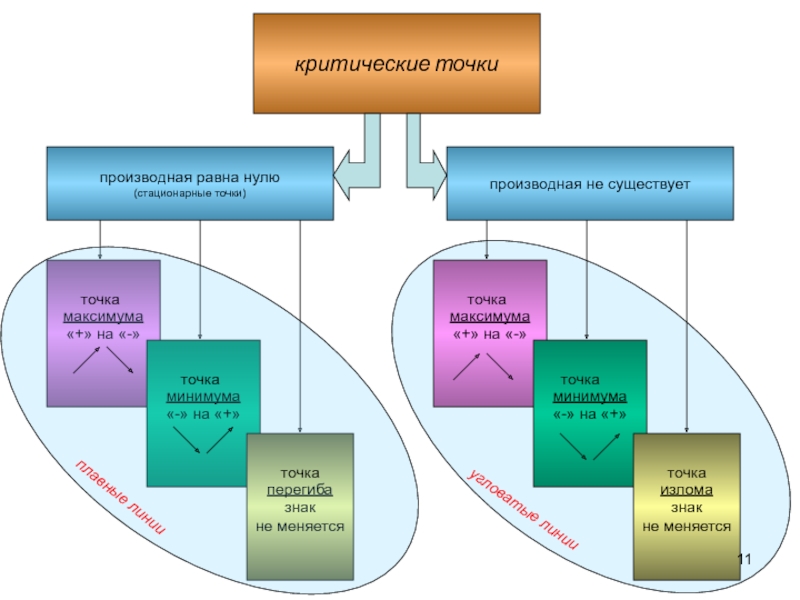
Слайд 11производная равна нулю
(стационарные точки)
критические точки
производная не существует
максимума
«+» на «-»
минимума
«-» на
«+»
перегиба
знак
не меняется
максимума
«+» на «-»
минимума
«-» на «+»
излома
знак
не меняется
плавные линии
угловатые
линииточка
точка
точка
точка
точка
точка
Слайд 12Достаточное условие существования экстремума функции:
Если при переходе через критическую
точку х0 функции f(x) ее производная меняет знак с «+»
на «-», то х0 – точка максимума функции f(x).Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «-» на «+», то х0 – точка минимума функции f(x).
3) Если при переходе через критическую точку х0 функции f(x) ее производная не меняет знака, то в точке х0 экстремума нет.
Слайд 14Схема исследования функции
Найти область определения функции;
Исследовать функцию на четность, нечетность,
периодичность;
Найти точки пересечения графика функции с осями координат;
Исследовать функцию на
монотонность, то есть найти промежутки возрастания и убывания функции;Найти точки экстремума и экстремальные значения функции;
Построить график функции.
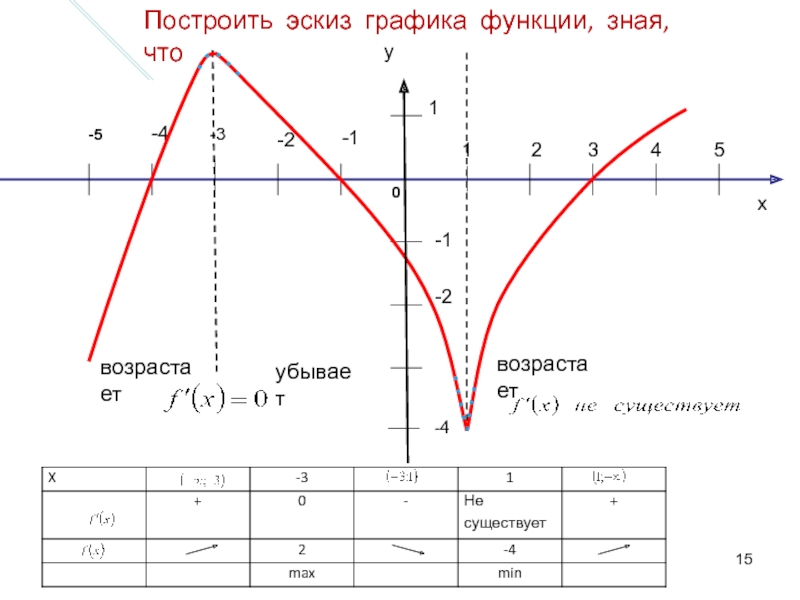
Слайд 15x
1
2
3
4
5
-1
-2
-4
-1
-2
1
-3
-5
0
возрастает
возрастает
убывает
Построить эскиз графика функции, зная, что
y
-4
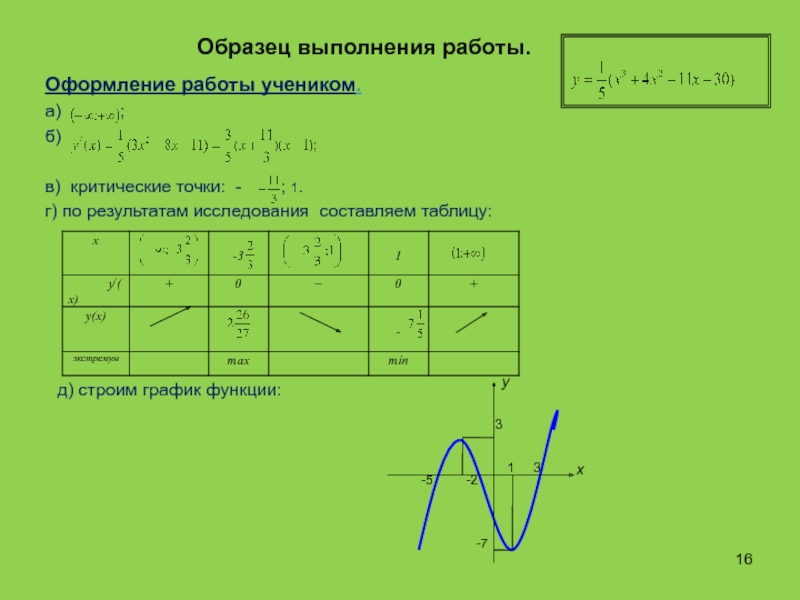
Слайд 16Образец выполнения работы.
Оформление работы учеником.
а)
;
б)
в) критические точки: - ; 1.
г)
по результатам исследования составляем таблицу:д) строим график функции:
1 3
х
у
-5 -2
3
-7
Слайд 18Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке
[a;b]
Чтобы найти наибольшее и наименьшее значения непрерывной функции f(x) на
промежутке [a;b], нужно вычислить её значения f(a) и f(b) на концах данного промежутка
вычислить её значения в критических точках, принадлежащих этому промежутку
выбрать из них наибольшее и наименьшее.
Записывают так: max f(x) и min f(x)
[a;b] [a;b]








![Применение производной к исследованию функций Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке [a;b] Чтобы Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке [a;b] Чтобы найти наибольшее и наименьшее](/img/thumbs/082c92fa3793c9c4c54f41400e9882b9-800x.jpg)



















