познакомить учащихся с квадратными уравнениями в общем виде;
- выработать умение
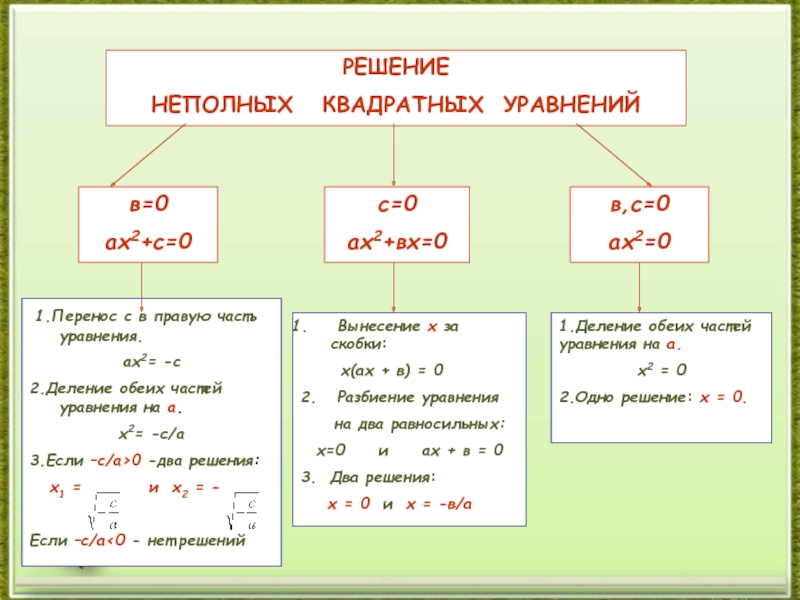
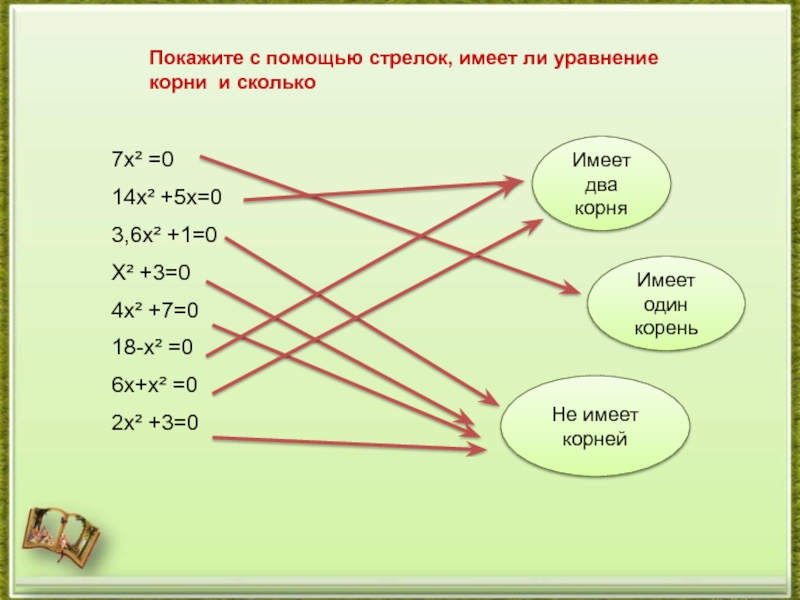
решать неполные квадратные уравнения;- способствовать выработке у школьников желания и потребности обобщения изучаемых фактов;
- развивать самостоятельность и творчество