Слайд 2 §3
Свойства
функции
Монотонность:
Возрастание;
убывание
нули функции
(значения аргумента,
в которых значение
Функции равно нулю)
непрерывность
периодичность
четность
нечетность
Экстремумы:
точка максимума,
точка минимума
выпуклость
Наибольшее и
наименьшее
значения
функции
Промежутки
знакопостоянства
(промежутки, в которых функция
принимает только положительные
или только отрицательные значения)
Слайд 3ОПРЕДЕЛЕНИЕ № 1
Функцию у = f(x) называют возрастающей на множестве
X Є D(f), если для любых двух элементов x1
и х2 множества Х, таких, что x1 < x2 , выполняется неравенство
f(x1) < f(x2).
Слайд 5ОПРЕДЕЛЕНИЕ № 2
Функцию у = f(x) называют убывающей на множестве
X Є D(f), если для любых двух элементов x1
и х2 множества Х, таких, что x1 < x2 , выполняется неравенство
f(x1) > f(x2).
Слайд 7Функция возрастает (убывает), если большему значению аргумента соответствует большее(меньшее) значение
функции.
Слайд 8Термины «возрастающая» и «убывающая» функции объединяют общим названием монотонная функция.
Исследование
функции на возрастание или убывание называют исследованием функции на монотонность.
Слайд 9ПРИМЕР № 1.
Исследовать на монотонность функцию
у = – 3х
+ 7.
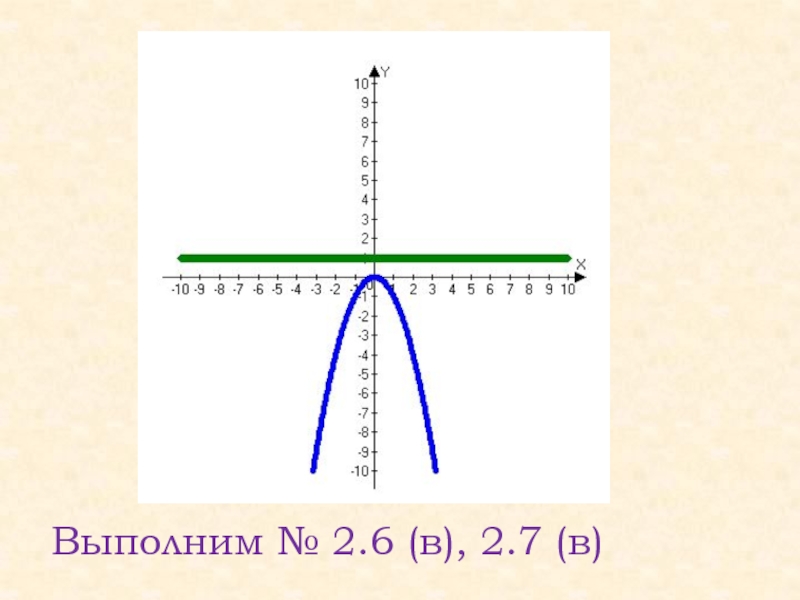
Выполним № 2.2(в,г), 2.4(в,г), 2.5(а,в)
Слайд 10ОПРЕДЕЛЕНИЕ № 3
Функция называется ограниченной снизу на множестве X Є
D(f), если существует такое число m, что для любого значения
х Є D(f) выполняется неравенство f(x) > m.
Слайд 12ОПРЕДЕЛЕНИЕ № 4
Функция называется ограниченной сверху на множестве X Є
D(f), если существует такое число m, что для любого значения
х Є D(f) выполняется неравенство f(x) < m.
Слайд 14ОПРЕДЕЛЕНИЕ № 5
Число m называется наименьшим значением функции у =
f(x) на множестве X Є D(f), если:
Существует число x0 Є
D(f) такое, что f(x0) = M;
Для любого значения х Є Х выполняется неравенство f(x) ≥ f(x0).
Слайд 15ОПРЕДЕЛЕНИЕ № 6
Число m называется наибольшим значением функции у =
f(x) на множестве X Є D(f), если:
Существует число x0 Є
D(f) такое, что f(x0) = M;
Для любого значения х Є Х выполняется неравенство f(x) ≤ f(x0).
Выполним № 2.8 – 2.10 (г)
Слайд 16СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
1. Область определения функции D(f).
2. Промежутки возрастания и
убывания (монотонность) функции.
3. Ограниченность функции.
4. Наибольшее и наименьшее значения функции.
5.
Непрерывность функции.
6. Область значений функции Е(f).
7. Выпуклость функции.
Слайд 17Линейная функция
функция вида y = k х + b
графиком функции является прямая
1. D( f ) = R;
E(
f ) = R;
k>0
k<0
k=0
Слайд 18Свойства функции
y=kx+b (k≠0)
1. Область определения D(f)
2. Монотонность
3. Ограниченность
4. Наибольшее и
наименьшее значения функции
5. Непрерывность
6. Область значений E(f)
7. Выпуклость
D(f)=(-∞;+∞).
Возрастает ,
если k>0 , убывает, если k<0.
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего ,ни наименьшего значения.
Функция непрерывна.
E(f) )=(-∞;+∞).
О выпуклости говорить не имеет смысла.
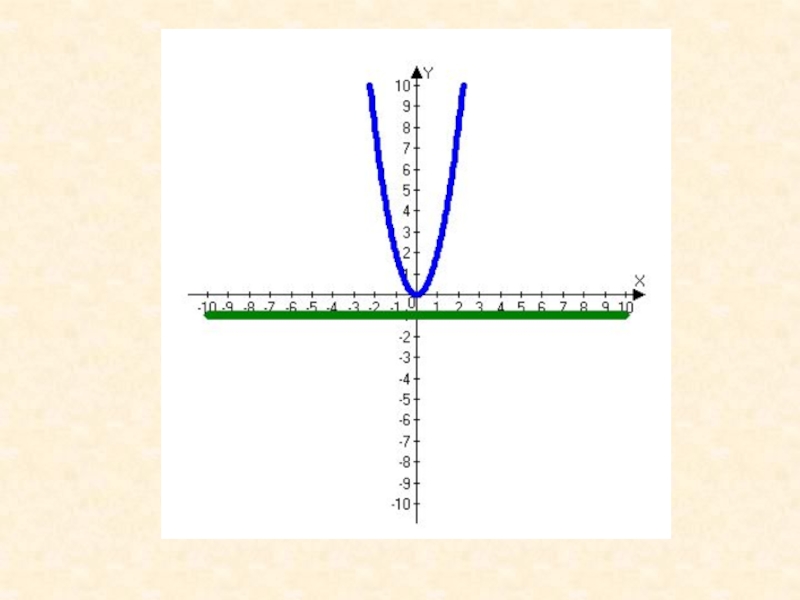
Слайд 19Квадратичная функция
функция вида y = kx², k>0; графиком функции
является парабола, ветви которой направлены вверх
Слайд 20Свойства функции
y=kx² (k>0)
1. Область определения
2. Монотонность
3. Ограниченность
4. Наибольшее и
наименьшее значения функции
5. Непрерывность
6. Область значений
7. Выпуклость
D(f)=(-∞;+∞).
Убывает
на луче (-∞;0], возрастает на луче[0;+∞).
Ограничена снизу, не ограничена сверху.
Yнаим.=0; Yнаиб. не существует.
Функция непрерывна.
E(f) )= [0;+∞).
Выпукла вниз.
Слайд 21Обратная пропорциональность
функция вида y = ; графиком
функции является гипербола
k
x
k>0
k
Слайд 22Свойства функции
y=k/x (k
наименьшее значения функции
5. Непрерывность
6. Область значений
7. Выпуклость
D(f)=(-∞;0)U(0;+∞).
Возрастает
на всей области определения.
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего ,ни наименьшего значения.
Функция непрерывна на открытом луче (-∞;0) и на открытом луче (0;+∞).
E(f) )=(-∞; 0)U(0;+∞).
Выпукла вверх при x>0 и выпукла вниз x<0.
Слайд 23Свойства функции
y=k/x (k>0)
1. Область определения
2. Монотонность
3. Ограниченность
4. Наибольшее и
наименьшее значения функции
5. Непрерывность
6. Область значений
7. Выпуклость
D(f)=(-∞;0)U(0;+∞).
Убывает на
всей области определения.
Не ограничена ни снизу, ни сверху.
Нет ни наибольшего ,ни наименьшего значения.
Функция непрерывна на открытом луче (-∞;0) и на открытом луче (0;+∞).
E(f) )=(-∞; 0)U(0;+∞).
Выпукла вверх при x<0 и выпукла вниз x>0.
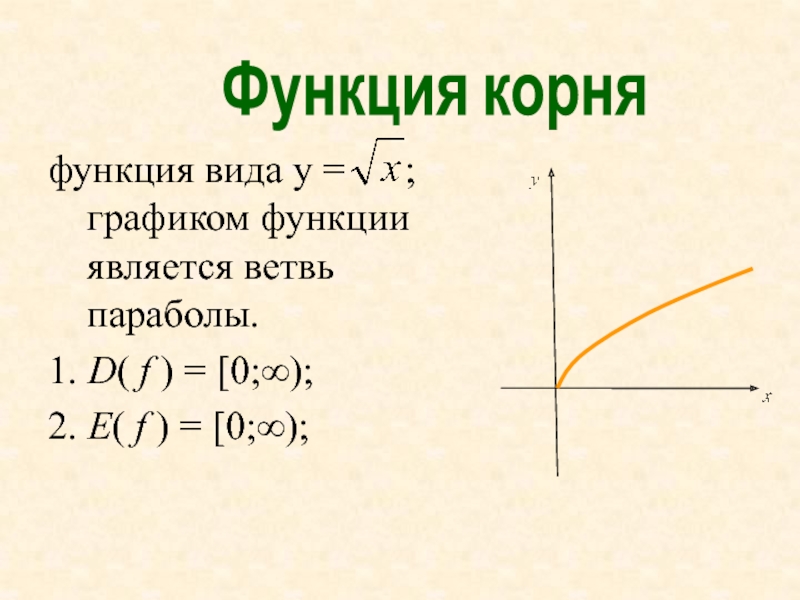
Слайд 24функция вида y = ; графиком функции является
ветвь параболы.
1. D( f ) = [0;∞);
2. E( f
) = [0;∞);
Функция корня
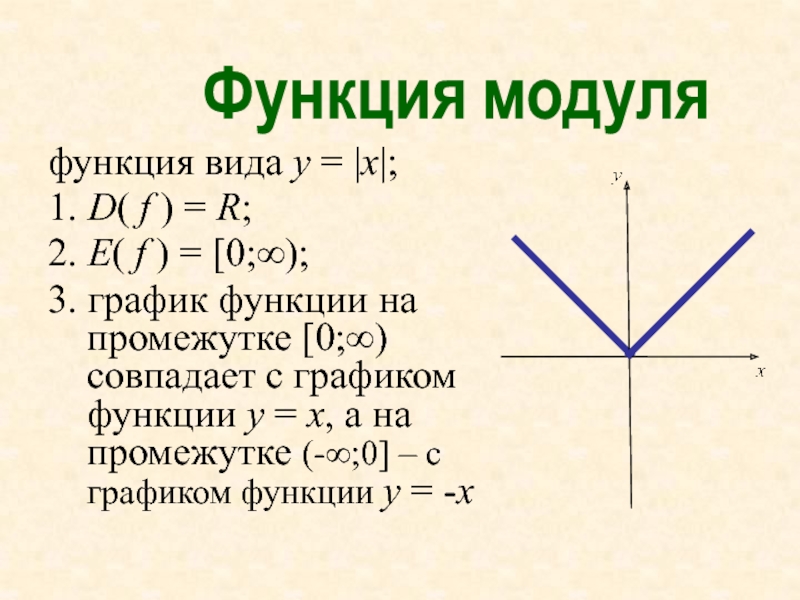
Слайд 25функция вида y = |x|;
1. D( f ) =
R;
2. E( f ) = [0;∞);
3. график функции
на промежутке [0;∞) совпадает с графиком функции у = х, а на промежутке (-∞;0] – с графиком функции у = -х
Функция модуля
Слайд 26Выполним № 2.13, 2.15
Домашнее задание
№ 2.2,2.4 – а
№
2.8 и 2.9 – а
№ 2.12
Слайд 28
Укажите область определения функции.
Слайд 29Укажите область определения функции
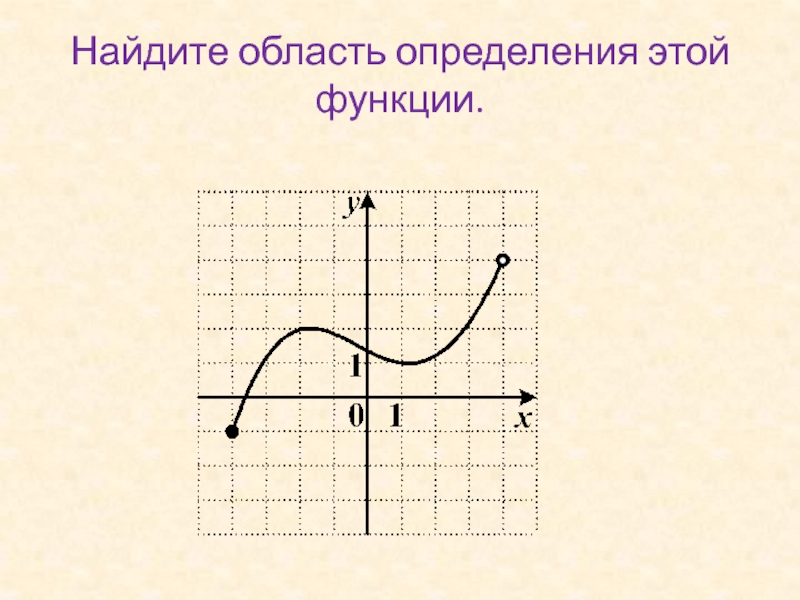
Слайд 30Найдите область определения этой функции.
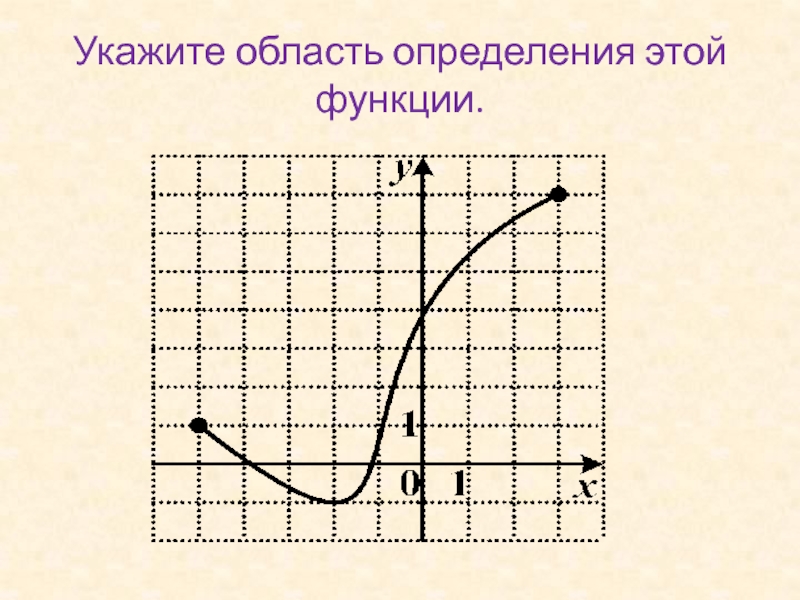
Слайд 31Укажите область определения этой функции.
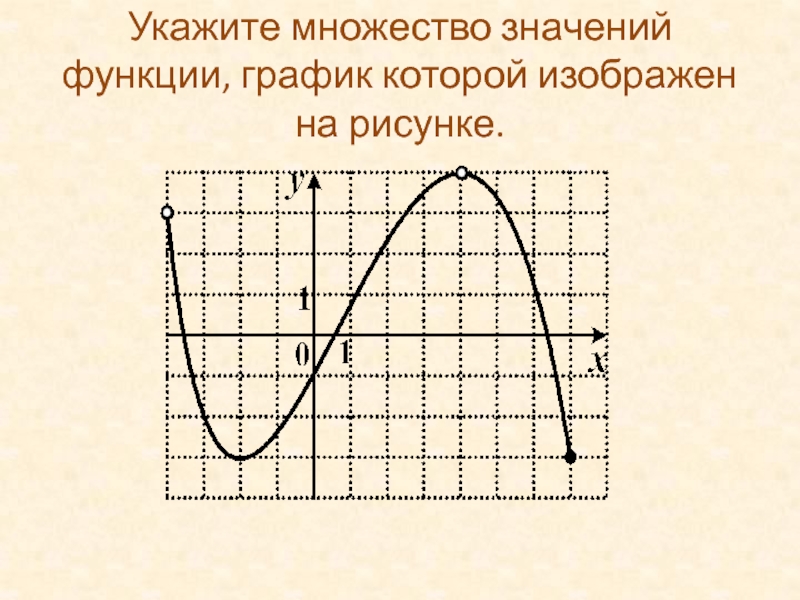
Слайд 32Укажите множество значений функции, график которой изображен на рисунке.
Слайд 33Укажите множество значений функции, график которой изображен на рисунке.
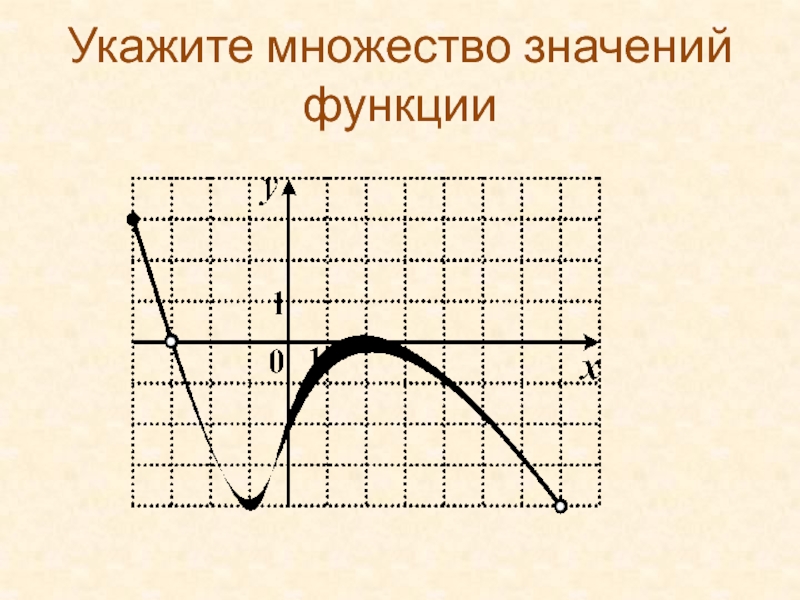
Слайд 34Укажите множество значений функции
Слайд 35Найдите множество значений этой функции.
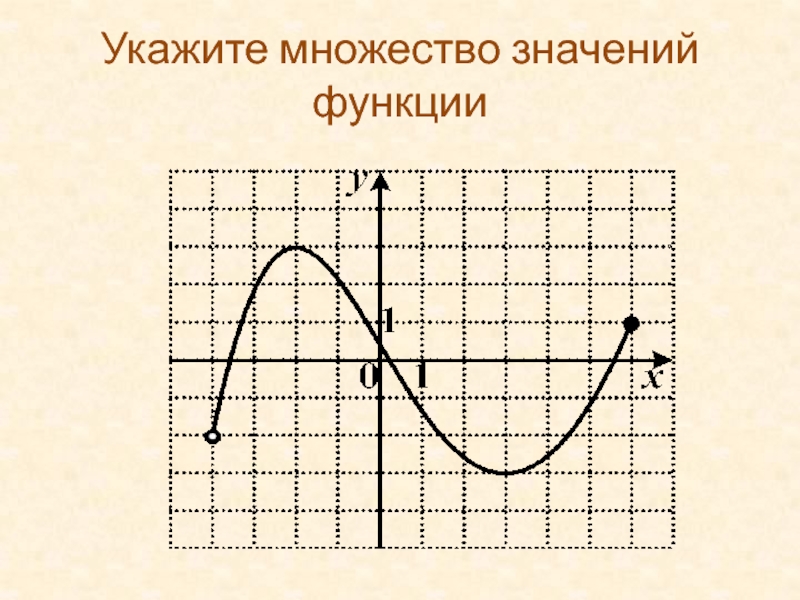
Слайд 36Укажите множество значений функции
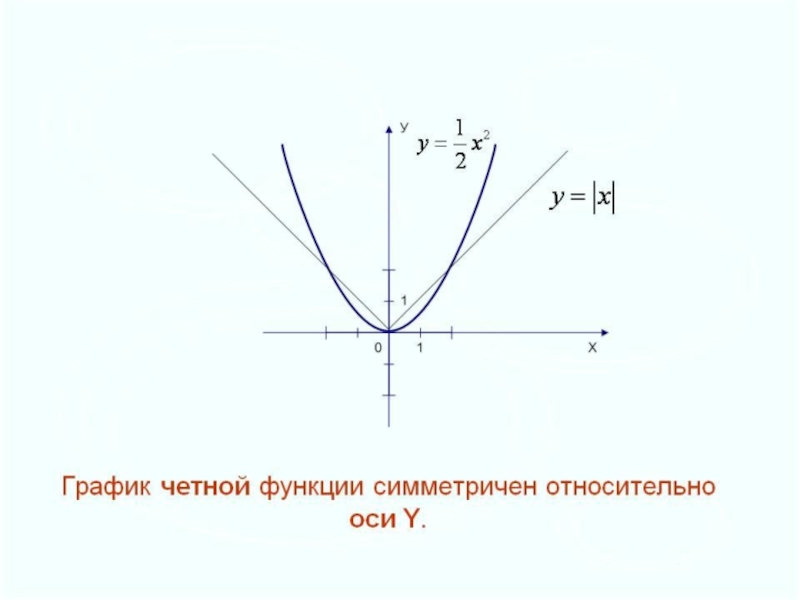
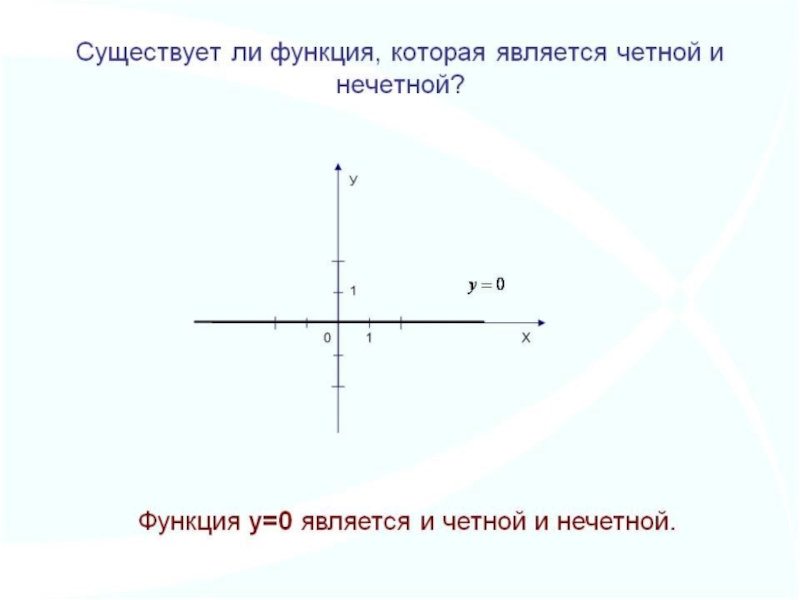
Слайд 37Функция у=f(x), называется чётной, если область её определения симметрична относительно
начала координат и выполняется равенство
f(-x)=f(x)
Функция у=f(x) называется нечётной, если область её определения симметрична относительно начала координат и выполняется равенство f(-x)=-f(x)
Четность и нечетность функций
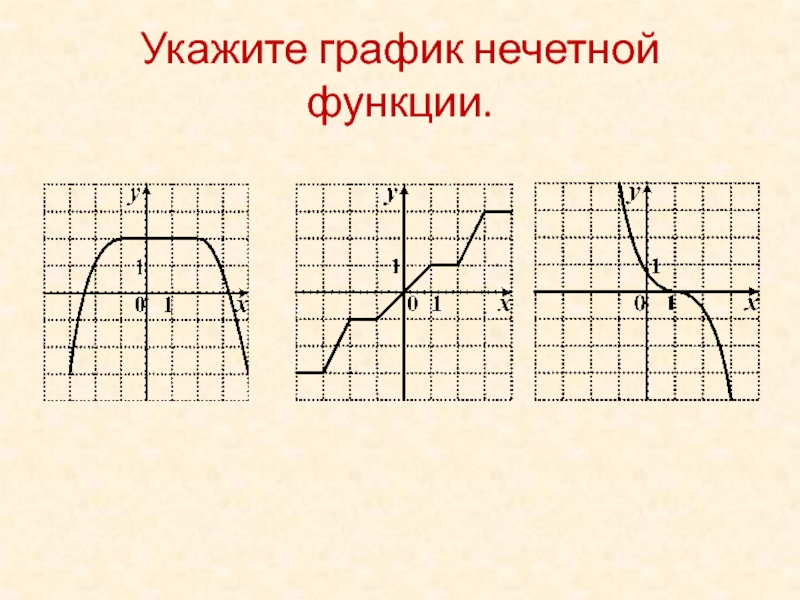
Слайд 41Укажите график нечетной функции.
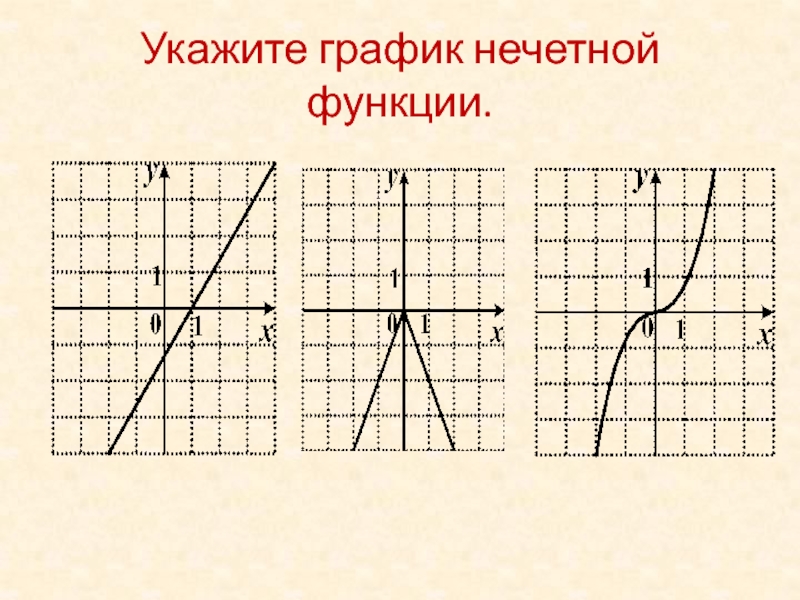
Слайд 42Укажите график нечетной функции.
Слайд 45Алгоритм исследования
Установить, симметрична ли область определения функции. Если нет,
то объяснить, что функция ни четная, ни нечетная. Если да,
то продолжить проверку.
Составить выражение f(-x).
Сравнить f(x) и f(-x)
Если f(x) = f(-x), то функция четная
Если f(-x) = -f(x), то функция нечетная
В другом случае функция является ни четной, ни нечетной.
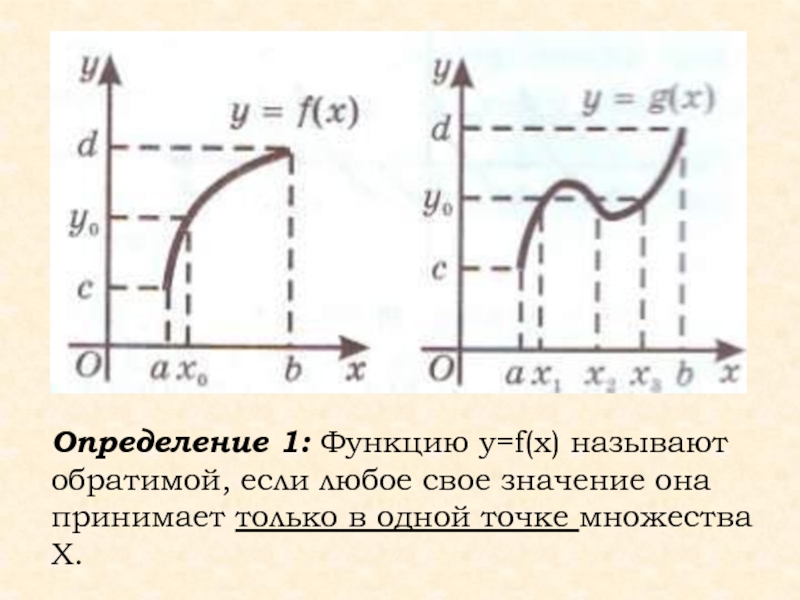
Слайд 47Определение 1: Функцию y=f(x) называют обратимой, если любое свое значение
она принимает только в одной точке множества X.
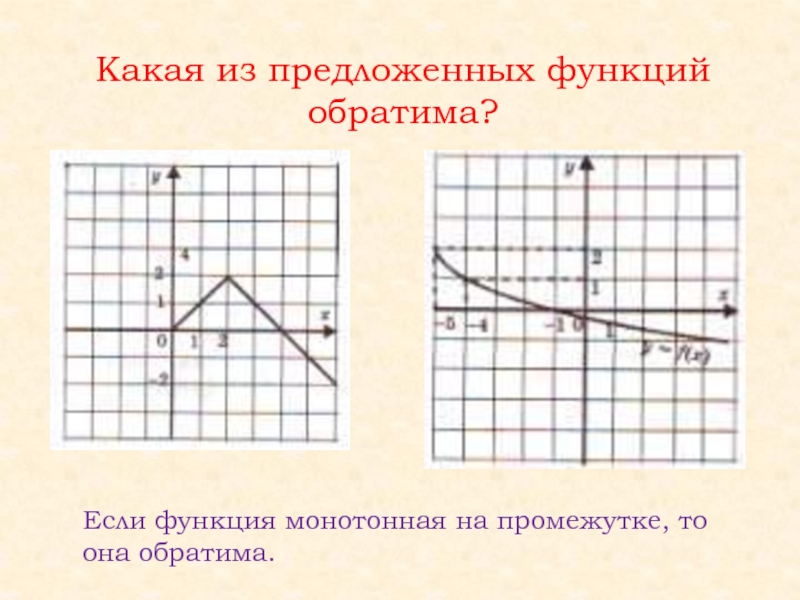
Слайд 48Какая из предложенных функций обратима?
Если функция монотонная на промежутке,
то она обратима.
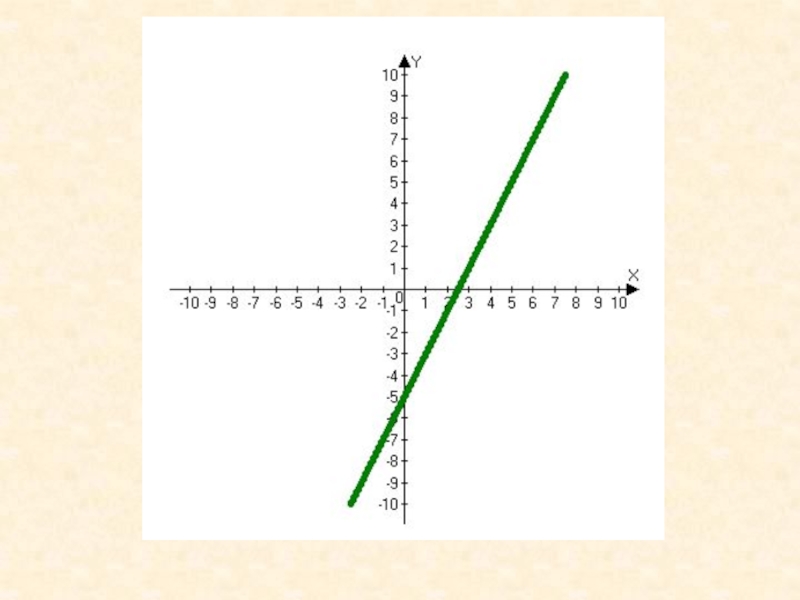
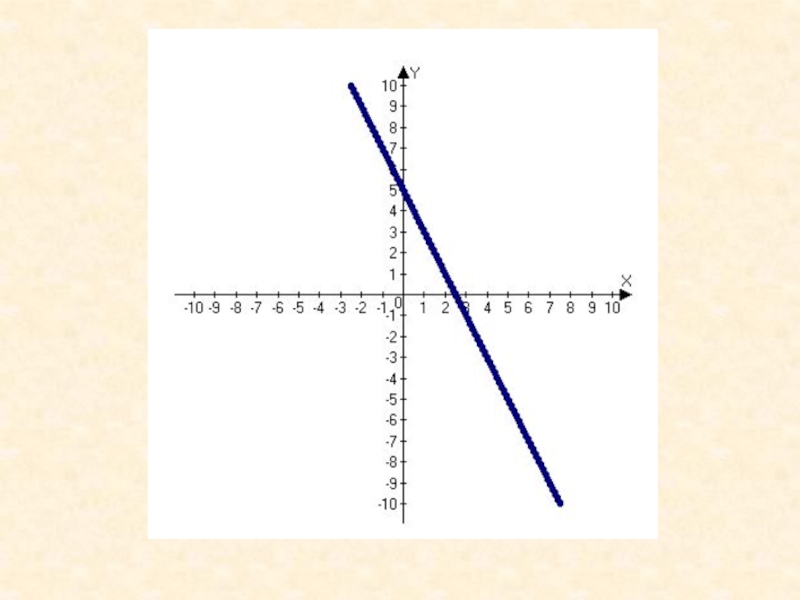
Слайд 49Пример 1:
Показать, что для функции y=5x-3 существует обратная функция,
и найти ее аналитическое выражение.
Решение. Линейная функция y=5x-3 определена на
R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R.
Чтобы найти ее аналитическое выражение, решим уравнение y=5x-3 относительно х; получим
Это и есть искомая обратная функция. Она определена и возрастает на R.
Слайд 50Пример 2: Показать, что для функции y=x2, х≤0 существует обратная
функция, и найти ее аналитическое выражение.
Функция непрерывна, монотонна в своей
области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, можно сделать вывод об аналитическом выражении для обратной функции.
0; графиком функции является парабола, ветви которой направлены вверх" alt="Квадратичная функция функция вида y = kx², k>0; графиком функции является парабола, ветви которой направлены вверх">
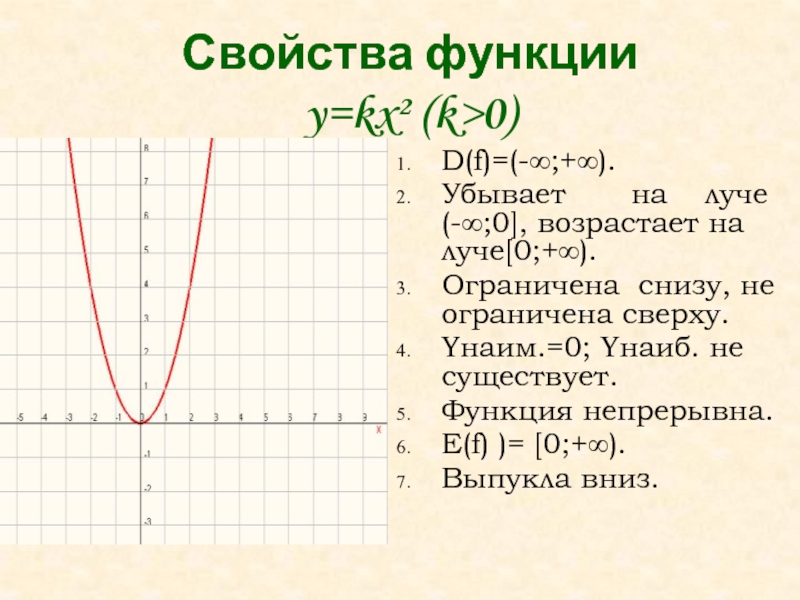0)1. Область определения 2. Монотонность3. Ограниченность4. Наибольшее и" alt="Свойства функции y=kx² (k>0)1. Область определения 2. Монотонность3. Ограниченность4. Наибольшее и наименьшее значения функции5. Непрерывность6. Область значений">
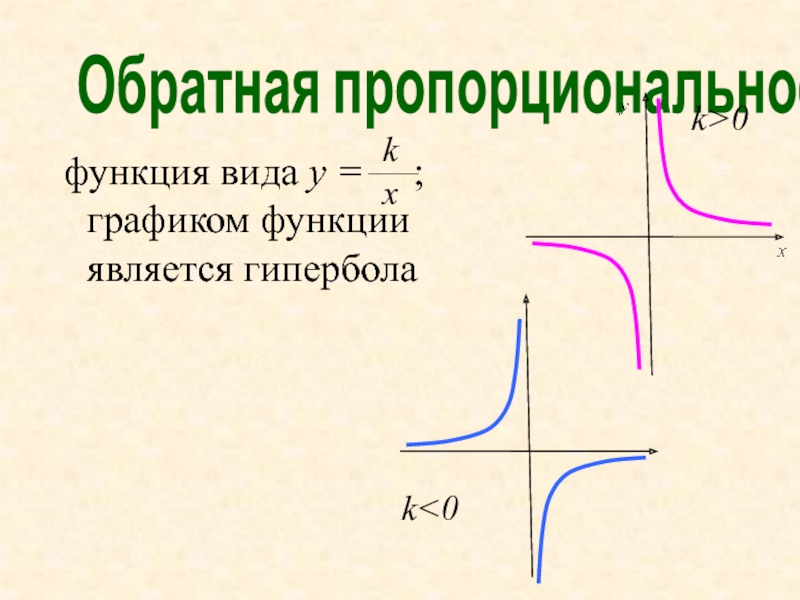0k" alt="Обратная пропорциональность функция вида y = ; графиком функции является гиперболаkxk>0k">
0)1. Область определения 2. Монотонность3. Ограниченность4. Наибольшее и" alt="Свойства функции y=k/x (k>0)1. Область определения 2. Монотонность3. Ограниченность4. Наибольшее и наименьшее значения функции5. Непрерывность6. Область значений">
