Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Знакомство с алгеброй. Числовые выражения 7 класс
Содержание
- 1. Знакомство с алгеброй. Числовые выражения 7 класс
- 2. Зарождение алгебры
- 3. Старинная задача о кроликах и фазанах
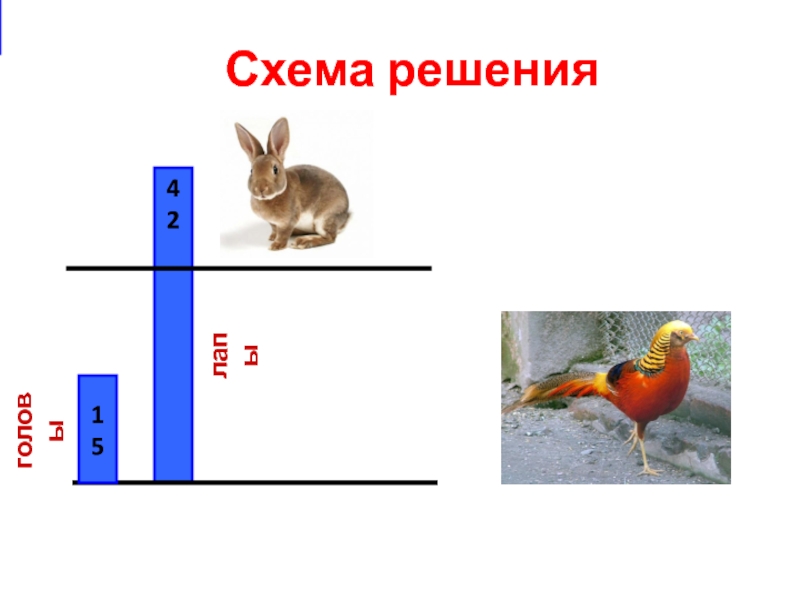
- 4. 15421512головылапыСхема решения
- 5. · 2=30 (лап)42-30=12 (лап лишних) – лапы кроликов12:2=6 (кроликов)15-6 = 9 (фазанов)Решение задачи
- 6. Решение задачи с помощью уравнения
- 7. Страницы историиПо-гречески «число» - арифмос.Почти все науки
- 8. Страницы историиДругой раздел математики посвящен различным фигурам
- 9. Страницы историиАбу Абдалах Мухаммед ибн Муса ал-Хорезми
- 10. Страницы историиПредполагают, что он родился в городе
- 11. Страницы историиАбу Абдалах Мухаммед ибн Муса ал-Хорезми
- 12. Аль-Хорезми первым написал книгу на арабском языке
- 13. Ал-джабра (восстановление)При решении уравненияЕсли в части одной,Безразлично
- 14. Ал-мукабала (противопоставление)Дальше смотрим в уравненье,Можно ль сделать
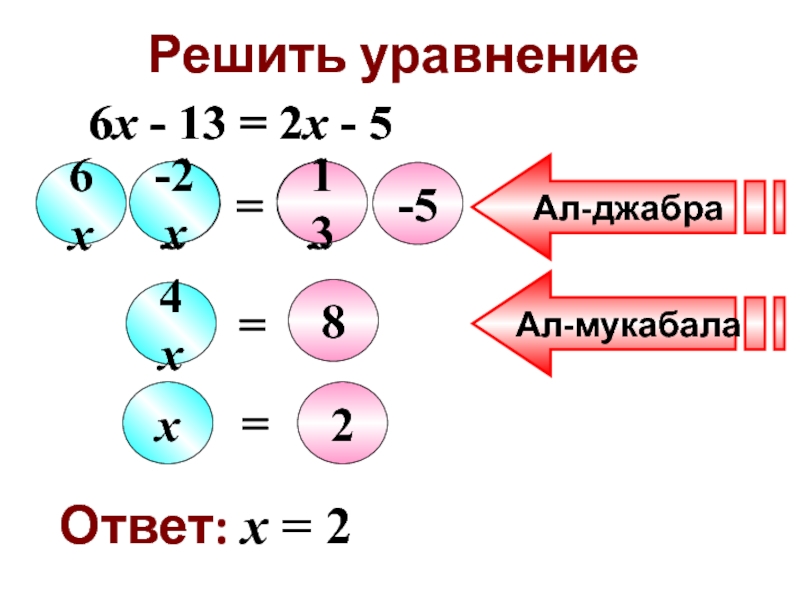
- 15. 6х-132х-5=13-2х4х=82=хАл-джабраАл-мукабалаРешить уравнение6х - 13 = 2х -
- 16. Отец алгебрыСам он слово «алгебра» не применял.
- 17. Отец алгебрыВиет четко разграничивал числа, величины и отношения, собрав их в некую систему "видов".
- 18. Отец алгебрыВ эту систему входили переменные, их
- 19. В процессе развития алгебра из
- 20. В основе алгебраического языка лежит непривычный «алфавит»1.
- 21. «Люди, незнакомые с алгеброй, не могут представить
- 22. Числовые выражения
- 23. Числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий (составленную со смыслом)
- 24. Числовое выражение – запись, включающая: 1)
- 25. То число, которое получается в результате упрощений числового выражения, называют значением числового выражения
- 26. Задание 1. Найдите значение числового выраженияЗначение числового выражения
- 27. 1. Порядок арифметических действий2. Переместительный закон сложения:
- 28. 6. Понятие обыкновенной дроби11. Понятие отрицательного числа12.
- 29. Дробь равна нулю, если числитель дроби равен нулю.
- 30. На ноль делить нельзя!Дробь не имеет смысла, если знаменатель дроби равен нулю.
- 31. Задание 2. Выясните, равна дробь нулю или она не имеет смысла?
- 32. Решение задачУстно:№ 1.1№ 1.2Письменно:№ 1.9 (а,б)№ 1.14
- 33. Домашнее заданиеПовторить правила действий с обыкновенными дробями, правила действий с положительными и отрицательными числами
- 34. Домашнее задание№ 1.3 (без вычислений)№ 1.5№ 1.10№
- 35. Список литературыМордкович, А. Г. Алгебра. 7 класс
- 36. Активные ссылки на использование изображения (URL –
- 37. Скачать презентанцию
Зарождение алгебры
Слайды и текст этой презентации
Слайд 1Знакомство с алгеброй
Числовые выражения
Учитель математики
МАОУ «Ангарский лицей №1»
Никифорова С.В.
г. Ангарск
Слайд 5 · 2=30 (лап)
42-30=12 (лап лишних) – лапы кроликов
12:2=6 (кроликов)
15-6
= 9 (фазанов)
Решение задачи
Слайд 6Решение задачи с помощью уравнения
Кролики
Фазаныкол-во х 15 - х
лапы 4х 2(15 – х)
4х+2(15-х)=42
4х+30-2х=42
4х-2х=42-30
2х=12
х=6 (кроликов)
Если х=6, то 15-х= 15-6=9 (фазанов)
Слайд 7Страницы истории
По-гречески «число» - арифмос.
Почти все науки зародились в Греции,
один из разделов математики получил греческое название «АРИФМЕТИКА»
Слайд 8Страницы истории
Другой раздел математики посвящен различным фигурам и их свойствам,
называется он ГЕОМЕТРИЕЙ
Гео – по-гречески
«Земля», а метрео - «меряю»А вот слово «АЛГЕБРА» не греческое
Слайд 9Страницы истории
Абу Абдалах Мухаммед ибн Муса ал-Хорезми
Выдающийся средневековый ученый,
внесший большой вклад в развитие математики, астрономии, математической географии.
Слайд 10Страницы истории
Предполагают, что он родился в городе Хиве.
Научной работой
аль-Хорезми в основном занимался в Багдаде.
Абу Абдалах Мухаммед ибн
Муса ал-Хорезми 
Слайд 11Страницы истории
Абу Абдалах Мухаммед ибн Муса ал-Хорезми
Его труды в
течение нескольких веков оказывали сильное влияние на ученых Востока и
Запада.
Слайд 12Аль-Хорезми первым написал книгу на арабском языке о решении уравнений
«Китаб мухтасар аль джебр ва-ал-мукабала»
Аль -
артикльКитаб - книга
Мухтасар – краткая
Джебр - восстановление
Ва – союз «и»
Ал - мукабала - противопоставление
Слайд 13Ал-джабра (восстановление)
При решении уравнения
Если в части одной,
Безразлично какой,
Встретится член отрицательный,
Мы
к обеим частям,
С этим членом сличив,
Равный член придадим,
Только с
знаком другим, - И найдем результат нам желательный
Слайд 14Ал-мукабала (противопоставление)
Дальше смотрим в уравненье,
Можно ль сделать приведенье,
Если члены в
нем подобны,
Сопоставить их удобно,
Вычтя равный член из них,
К одному приводим
их.
Слайд 156х
-13
2х
-5
=
13
-2х
4х
=
8
2
=
х
Ал-джабра
Ал-мукабала
Решить уравнение
6х - 13 = 2х - 5
6х - 13
= 2х - 5
Ответ: х = 2
Слайд 16Отец алгебры
Сам он слово «алгебра» не применял. И называл он
её «аналитическим искусством», то есть искусством исследования
Франсуа Виет
(1540-1603 гг.)
Слайд 17Отец алгебры
Виет четко разграничивал числа, величины и отношения, собрав их
в некую систему "видов".
Слайд 18Отец алгебры
В эту систему входили переменные, их корни, квадраты, кубы
и т. д.
Для этих видов Виет дал специальную символику,
обозначив их прописными буквами латинского алфавита. 
Слайд 19 В процессе развития алгебра из науки об уравнениях
преобразовалась в науку об операциях, более или менее сходных с
действиями над числами.Современная алгебра – один из разделов математики
Слайд 20В основе алгебраического языка лежит непривычный «алфавит»
1. Числа
2. Буквы латинского
и греческого алфавита
3. Знаки операций: + ,
-, ·, :4. Скобки ( , )
5. Знак равенства =
6. Знаки неравенств: <, > , ,
Вот его буквы:
Слайд 21«Люди, незнакомые с алгеброй, не могут представить себе тех удивительных
вещей, которых можно достигнуть … при помощи названной науки»
Г.В. Лейбниц
Слайд 23Числовым выражением называют всякую запись, составленную из чисел и знаков
арифметических действий (составленную со смыслом)
Слайд 24Числовое выражение – запись, включающая: 1) числа; 2) знаки арифметических действий; 3)
составлена со смыслом
Слайд 25То число, которое получается в результате упрощений числового выражения, называют
значением числового выражения
Слайд 271. Порядок арифметических действий
2. Переместительный закон сложения: а + b
= b + a
3. Переместительный закон умножения: аb =
ba 4. Сочетательный закон сложения: а + b + с = (а + b) + с = а + (b + с)
5. Сочетательный закон умножения: аbс = (аb)с = а(bс)
Слайд 286. Понятие обыкновенной дроби
11. Понятие отрицательного числа
12. Правила действий с
положительными и отрицательными числами
7. Арифметические операции с обыкновенными дробями
9. Понятие
десятичной дроби10. Арифметические операции с десятичными дробями
8. Основное свойство обыкновенной дроби
Слайд 32Решение задач
Устно:
№ 1.1
№ 1.2
Письменно:
№ 1.9 (а,б)
№ 1.14 (а,б)
№ 1.15 (а,б)
№
1.16 (а,б)
№ 1.18 (а)
№ 1.19 (а)
№ 1.51
Слайд 33Домашнее задание
Повторить правила действий с обыкновенными дробями, правила действий с
положительными и отрицательными числами
Слайд 34Домашнее задание
№ 1.3 (без вычислений)
№ 1.5
№ 1.10
№ 1.14 (в, г)
№
1.15 (в, г)
№ 1.16 (в, г)
№ 1.19 (б)
№ 1.20 (б)
Слайд 35Список литературы
Мордкович, А. Г. Алгебра. 7 класс : в 2
ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.
Г. Мордкович. - М. : Мнемозина, 2015.Алгебра. 7 класс : в 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович [и др.]; под ред. А. Г. Мордковича. - М.: Мнемозина, 2015.
Слайд 36Активные ссылки на использование изображения (URL – адреса).
Рисунок кролика http://krolikoved.ru/sites/default/files/images/0_0.jpg
Рисунок
фазана http://www.zoopark-rostov.ru/userfiles/image/zolotoi%20fazan.jpg
Изображение Абу Абдалаха Мухаммеда ибн Муса ал-Хорезми http://www.asia-travel.uz/images/uzbekistan/outstanding-people/al-horezmi.jpg
Изображение Франсуа
Виета http://to-name.ru/images/biography/viet-fransua.jpg
