Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Содержание
- 1. РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
- 2. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ: Какую функцию мы стали
- 3. Решение линейного неравенства 2х – 4 >0
- 4. «РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИС ОДНОЙ ПЕРЕМЕННОЙ»тема урока:
- 5. Изучить определение неравенства второй степени с одной
- 6. Слайд 6
- 7. РАБОТА С ЗЛЕКТРОННЫМИ ОБРАЗОВАТЕЛЬНЫМИ РЕСУРСАМИ: (по парам)Перейдите
- 8. - 2ПРИМЕР 1.
- 9. ПРИМЕР 2
- 10. ПРИМЕР 3.
- 11. ПРИМЕР 4. Решить неравенство:
- 12. Слайд 12
- 13. Итак, для решения неравенств вида ах² +
- 14. 3) Находят на оси Х промежутки, для
- 15. Работа с помощью программы
- 16. Слайд 16
- 17. Найдите по графику: а) нули функции;- 4
- 18. http://fcior.edu.ru/catalog/osnovnoe_obshee?class=9&discipline_oo=5&moduletypes%5B0%5D=&page=14 Решение неравенств второй степени с одной
- 19. Домашнее задание: 1 уровень – п. 14,
- 20. http://fcior.edu.ru/catalog/osnovnoe_obshee?class=9&discipline_oo=5&moduletypes%5B0%5D=&page=14 Решение неравенств второй степени с одной
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
Какую функцию мы стали изучать недавно?
Дайте определение
этой функции. (Запись на доске)
В каком виде ещё можно записать
эту функцию? (Запись на доске)Что является графиком этих функций?
Как найти вершины этих парабол?
От чего зависит направление ветвей параболы?
Что такое нули функции?
Как их найти по графику функции?
Как найти нули по формуле функции?
В какой части координатной плоскости находится график функции, если: а) f(x) > 0; б) f(x) < 0?
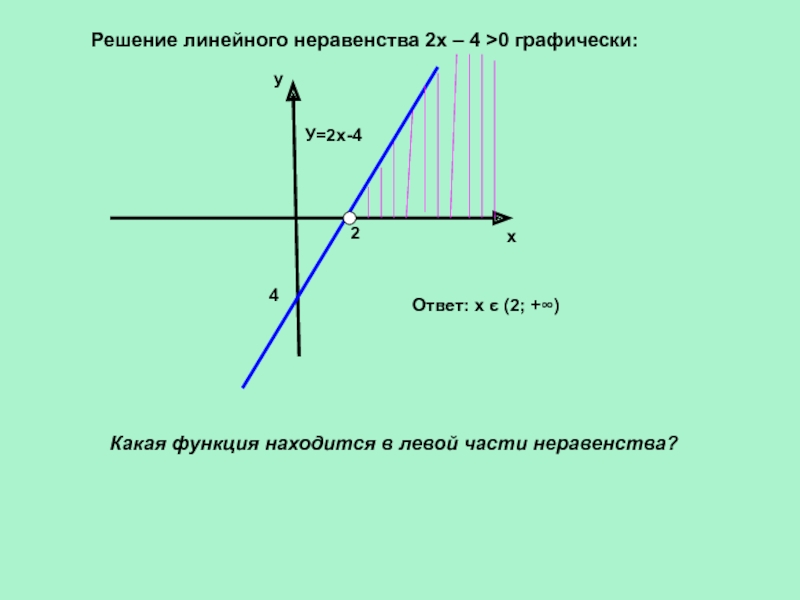
Слайд 3Решение линейного неравенства 2х – 4 >0 графически:
2
4
у
х
Ответ: х є
(2; +∞)
Какая функция находится в левой части неравенства?
У=2х-4
Слайд 5Изучить определение неравенства второй степени с одной переменной.
Ознакомиться с алгоритмом
решения неравенств второй степени с одной переменной.
цели урока:
Слайд 6
Неравенства вида
ах² + bx + c > 0 и
где х – переменная, а а, b и с – некоторые числа,
называются неравенствами второй степени
с одной переменной.
ах² + bx + c < 0
определение:
Слайд 7РАБОТА С ЗЛЕКТРОННЫМИ ОБРАЗОВАТЕЛЬНЫМИ РЕСУРСАМИ: (по парам)
Перейдите по данной гиперссылке:
http://fcior.edu.ru/catalog/osnovnoe_obshee?class=9&discipline_oo=5&moduletypes%5B0%5D=&page=14
Решение неравенств второй степени с одной переменной. И1
Выполните задания
№1, №2, №3 (решения заданий запишите в тетрадь)Слайд 8
- 2
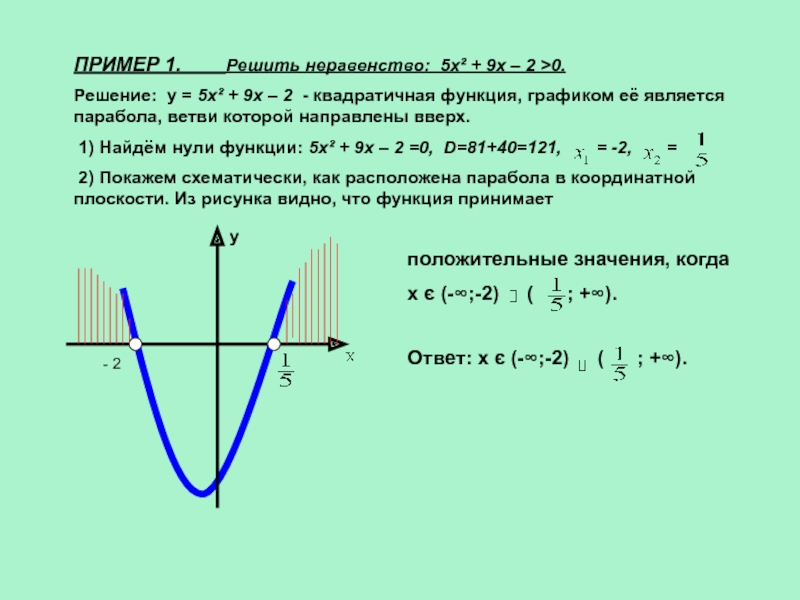
ПРИМЕР 1. Решить неравенство: 5x²
+ 9x – 2 >0.
Решение: у = 5x² + 9x
– 2 - квадратичная функция, графиком её является парабола, ветви которой направлены вверх.1) Найдём нули функции: 5x² + 9x – 2 =0, D=81+40=121, = -2, =
2) Покажем схематически, как расположена парабола в координатной плоскости. Из рисунка видно, что функция принимает
положительные значения, когда
х є (-∞;-2) ( ; +∞).
Ответ: х є (-∞;-2) ( ; +∞).
у
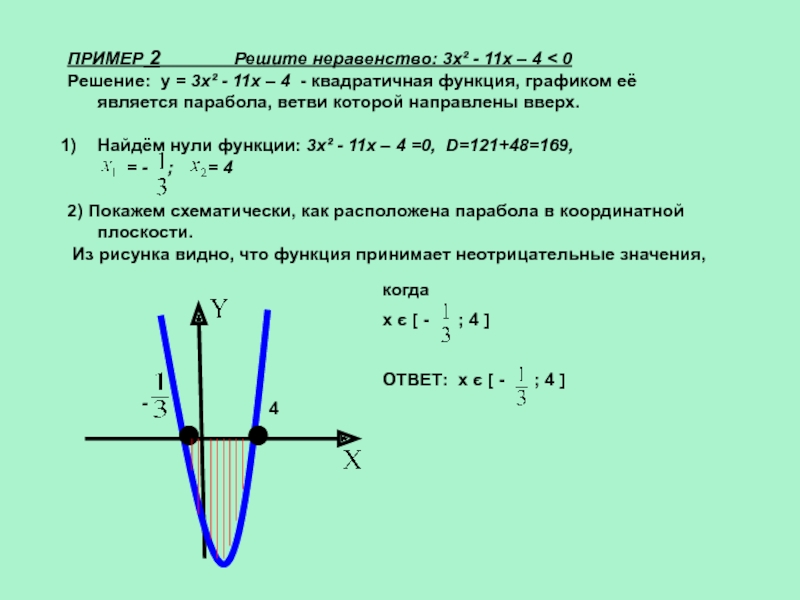
Слайд 9ПРИМЕР 2 Решите
неравенство: 3х² - 11х – 4 < 0
Решение: у
= 3x² - 11x – 4 - квадратичная функция, графиком её является парабола, ветви которой направлены вверх.Найдём нули функции: 3x² - 11x – 4 =0, D=121+48=169,
= - ; = 4
2) Покажем схематически, как расположена парабола в координатной плоскости.
Из рисунка видно, что функция принимает неотрицательные значения,
-
4
когда
х є [ - ; 4 ]
ОТВЕТ: х є [ - ; 4 ]
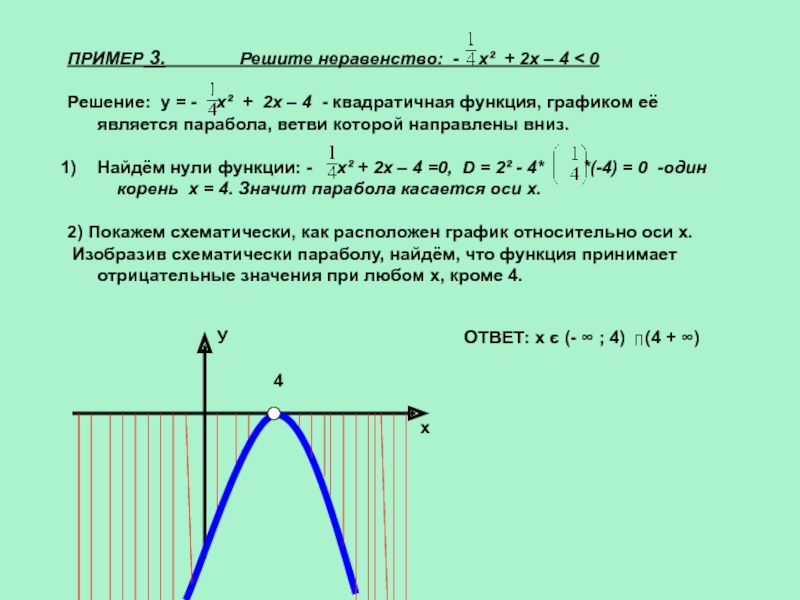
Слайд 10ПРИМЕР 3. Решите
неравенство: - х² + 2х – 4 < 0
Решение: у = - x² + 2x – 4 - квадратичная функция, графиком её является парабола, ветви которой направлены вниз.
Найдём нули функции: - x² + 2x – 4 =0, D = 2² - 4* *(-4) = 0 -один
корень х = 4. Значит парабола касается оси х.
2) Покажем схематически, как расположен график относительно оси х.
Изобразив схематически параболу, найдём, что функция принимает отрицательные значения при любом х, кроме 4.
ОТВЕТ: х є (- ∞ ; 4) (4 + ∞)
У
х
4
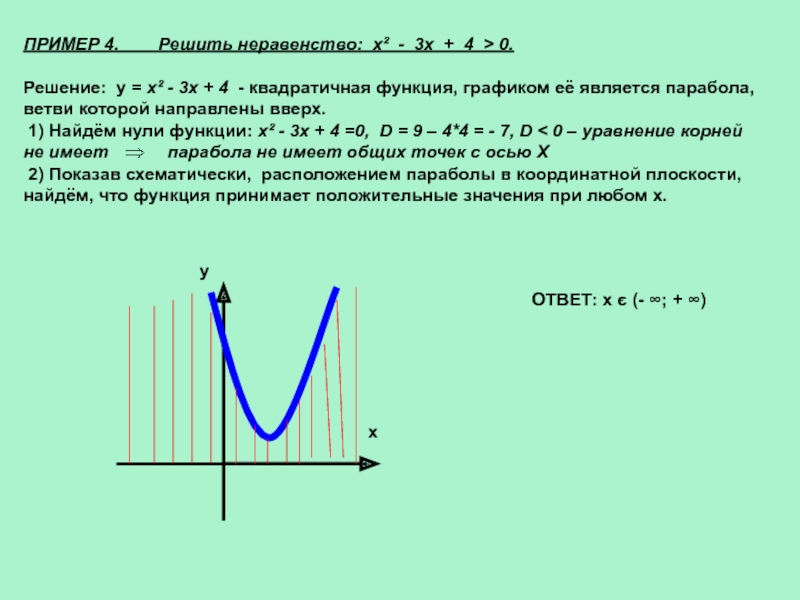
Слайд 11ПРИМЕР 4. Решить неравенство: x² - 3x
+ 4 > 0.
Решение: у = x² - 3x +
4 - квадратичная функция, графиком её является парабола, ветви которой направлены вверх.1) Найдём нули функции: x² - 3x + 4 =0, D = 9 – 4*4 = - 7, D < 0 – уравнение корней не имеет парабола не имеет общих точек с осью Х
2) Показав схематически, расположением параболы в координатной плоскости,
найдём, что функция принимает положительные значения при любом х.
ОТВЕТ: х є (- ∞; + ∞)
х
у
Слайд 12
ФИЗКУЛЬТМИНУТКА
ЗАРЯДКА ДЛЯ…
1. Зажмурить глаза. Открыть глаза (5 раз).
2. Круговые движения глазами. Головой не вращать (10 раз).
3. Не поворачивая головы, отвести глаза как можно дальше влево. Не моргать. Посмотреть прямо. Несколько раз моргнуть. Закрыть глаза и отдохнуть. То же самое вправо (2-3 раза).
4. Смотреть на какой-либо предмет, находящийся перед собой, и поворачивать голову вправо и влево, не отрывая взгляда от этого предмета (2-3 раза).
5. Смотреть в окно вдаль в течение 1 минуты.
6. Поморгать 10-15 с. Отдохнуть, закрыв глаза.
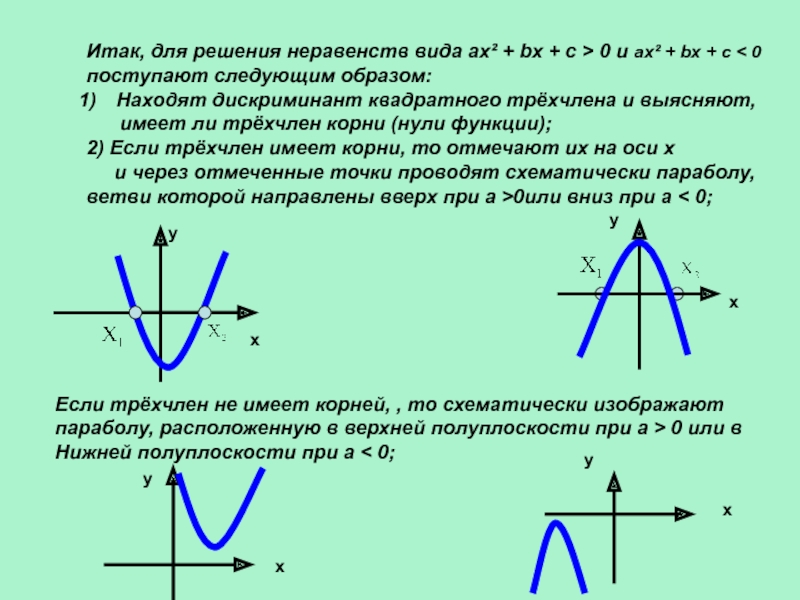
Слайд 13Итак, для решения неравенств вида ах² + bx + c
> 0 и ах² + bx + c < 0
поступают следующим образом:
Находят дискриминант квадратного трёхчлена и выясняют,
имеет ли трёхчлен корни (нули функции);
2) Если трёхчлен имеет корни, то отмечают их на оси х
и через отмеченные точки проводят схематически параболу,
ветви которой направлены вверх при а >0или вниз при а < 0;
х
у
х
у
Если трёхчлен не имеет корней, , то схематически изображают
параболу, расположенную в верхней полуплоскости при а > 0 или в
Нижней полуплоскости при а < 0;
х
у
х
у
Слайд 143) Находят на оси Х промежутки, для которых точки расположены
выше
оси Х (если решают неравенство ах² + bx + c
> 0 ) илиниже оси Х (если решают неравенство ах² + bx + c < 0 )
http://fcior.edu.ru/catalog/osnovnoe_obshee?class=9&discipline_oo=5&moduletypes%5B0%5D=&page=14
Решение неравенств второй степени с одной переменной. И1
Работа в парах: прочитайте и разберите задания №4, №5, №6, №7.
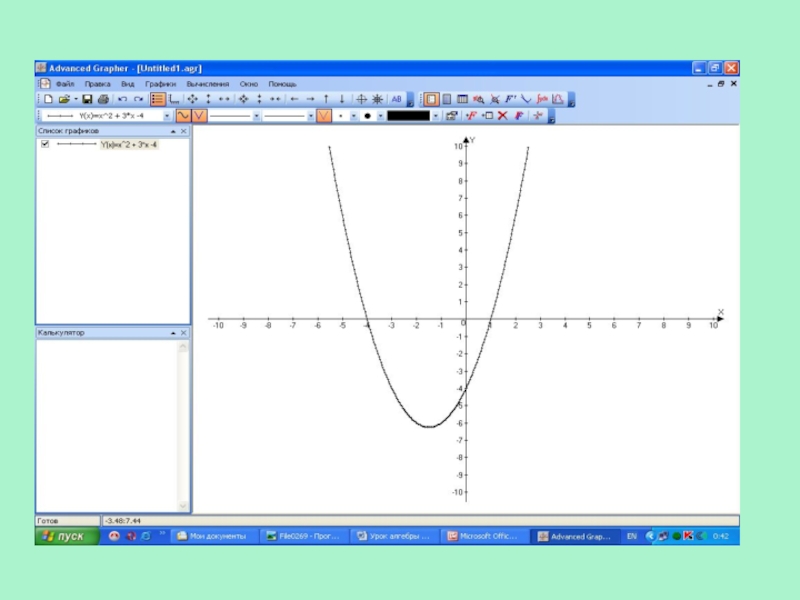
Слайд 15Работа с помощью программы
Advanced Grapher
Запишите неравенство x² + 3x – 4 > 0. Назовите функцию, которая находится слева от знака неравенства
y = x² + 3x – 4
С помощью программы Advanced Grapher постройте график этой функции.
Слайд 17Найдите по графику:
а) нули функции;
- 4 и 1
б) значения аргумента, при которых функция принимает положительные значения;
(−∞; -
4) ∪ (1;+∞) в) значения аргумента, при которых функция принимает отрицательные значения.
(−4;1)
Запишите в тетрадь решение неравенств x² + 3x – 4 > 0 и x² + 3x – 4 < 0.
Слайд 18http://fcior.edu.ru/catalog/osnovnoe_obshee?class=9&discipline_oo=5&moduletypes%5B0%5D=&page=14
Решение неравенств второй степени с одной переменной. П1
Решение неравенств
второй степени с одной переменной. П2
РАБОТА С ЗЛЕКТРОННЫМИ ОБРАЗОВАТЕЛЬНЫМИ РЕСУРСАМИ:
желаю
успеха!Слайд 19Домашнее задание: 1 уровень – п. 14, № 305(а), 309(а.
в, д), 2 уровень п. 14, №313(а, в), 315 (б,
г), 3 уровень №318, 320(б)домашнее задание:
Слайд 20
http://fcior.edu.ru/catalog/osnovnoe_obshee?class=9&discipline_oo=5&moduletypes%5B0%5D=&page=14
Решение неравенств второй степени с одной переменной. И1
http://fcior.edu.ru/catalog/osnovnoe_obshee?class=9&discipline_oo=5&moduletypes%5B0%5D=&page=14
Решение
неравенств второй степени с одной переменной. П1
http://skosh.ru/index.php/fizkultminutki
Учебник Алгебра 9
класс под редакцией С. А. ТеляковскогоЮ. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова
Используемая литература:
Программа Advanced Grapher